Uniswap v3 수학 통찰: 옵션이 포지션과 어떻게 결합되는가

撰文：ck.eth

编译：Lylia， Antalpha Labs

원 시리즈는 총 여섯 부분으로 구성되어 있으며, 이는 다섯 번째 부분으로 옵션이 포지션과 결합되는 방법을 계속 소개합니다. 이 시리즈의 이전에 설명된 포지션 전략에 대한 이해가 필요합니다. 더 많은 사람들이 Uniswap V3에 대한 유용한 정보를 접근하고 이해할 수 있도록 시리즈 기사를 번역하였습니다. 이를 통해 중국어 독자들이 Uniswap v3 메커니즘과 투자 전략 선택에 대해 더 깊이 이해할 수 있기를 바랍니다. 이 번역을 읽는 동안 언제든지 원문을 참조하여 더 많은 세부 정보를 얻을 수 있습니다.

Uniswap 수익 볼록성 위험의 비선형성 / Theta-Gamma 변동성. https://www.math3d.org/WvsEXvTWD

간단히 말해서:

• Uniswap v2와 v3에 대한 그리스 솔루션을 보여줍니다.
• 대화형 desmos 파일에서 Uniswapv3를 사용하여 아시아 옵션, 유럽 옵션 및 Bachelier 옵션을 헤지하는 솔루션을 제공합니다.
• desmos를 사용하여 LP 헤지 누적 전략을 보여줍니다.
• LVR을 초래하는 역사와 대체 유도에 대해 설명합니다.

그리스 매개변수 - Uniswap v2

100%를 LP 포지션에 할당하는 것보다 일부를 X 자산에 할당하고 나머지를 X 자산을 공매도하여 발산 손실을 줄이는 것이 더 좋습니다. 결과적으로 지불 구조가 절벽에서 언덕으로 전환됩니다. Guillaume Lambert가 보여준 바와 같이: 그리스 매개변수는 LP 포지션의 가치가 다른 변수(예: 시간, 변동성 및 이자율)에 대해 얼마나 민감한지를 알려줍니다. 우리는 4부에서 델타와 감마를 소개했습니다. LP 그리스 매개변수는 유용합니다. 왜냐하면 이를 옵션의 그리스 매개변수와 일치시켜 가격 차이를 상쇄할 수 있기 때문입니다. 예를 들어, 가격 변동, 변동성 변화 또는 시간 경과에 따른 효과인 델타와 감마입니다. 그리스 매개변수의 수치는 다양한 요소가 LP 포지션 가격에 미치는 영향을 알려줍니다.

v2의 대화형 desmos 파일: https://www.desmos.com/calculator/inwy6djhhm

유의해야 할 점은 옵션에 비해 Uniswap의 그리스 매개변수가 LP 포지션 가격이 하락할 때 무한대로 수렴한다는 것입니다. 위 그림에서 x=0에서 점선으로 표시되어 있습니다. 이러한 꼬리 위험을 줄이기 위해 v3에서 집중 범위를 사용할 수 있습니다.

그리스 매개변수 - 집중 LP 범위 v3

univ3 그리스 매개변수의 desmos 파일: https://www.desmos.com/calculator/l8sqzlwkf5

범위 pa (하한) ~ pb (상한)를 집중시킬수록 우리의 델타 Δ와 감마 Γ는 더욱 민감해집니다. 감마가 음수라는 점에 유의해야 하며, 이는 우리의 LP 지불이 오목한 검은 형태를 가지고 있음을 의미합니다. 우리의 세타 /Θ / 예상 비용도 증가하며, 이자율 민감도 ρ는 기본적으로 영향을 받지 않습니다.

하지만, 개별 LP 포지션의 지불 그래프가 옵션과 일치할 수 있지만, 다른 그리스 매개변수는 일치하지 않을 수 있습니다.

LP 그리스 매개변수는 일반 옵션과 같지 않습니다: https://www.desmos.com/calculator/nyuw7sybin

여기에서 우리는 단일 LP 범위의 콜 옵션을 가지고 있지만, 다른 그리스 매개변수는 고정되어 있지 않습니다.

사용할 수 있는 기술은 LP 포지션을 헤지하는 방법을 찾으려 하기보다는, 먼저 시장에서 실행 가격(K)과 암묵적 변동성(σ_iv) 및 만기 시간(t)을 가진 옵션을 찾아야 한다는 것입니다. 그 후, 로그 정규 분포를 따르는 일련의 LP 포지션을 구축할 수 있습니다. 이는 Dan Robinson의 Uniswap v3에 대한 정규 분포 유동성 지문에서 영감을 받았습니다 ^[1]^. 가격 공간에서 LP 포지션이 로그 정규 분포의 세분화와 일치하도록 허용하여 그리스 매개변수를 부드럽게 처리할 수 있습니다:

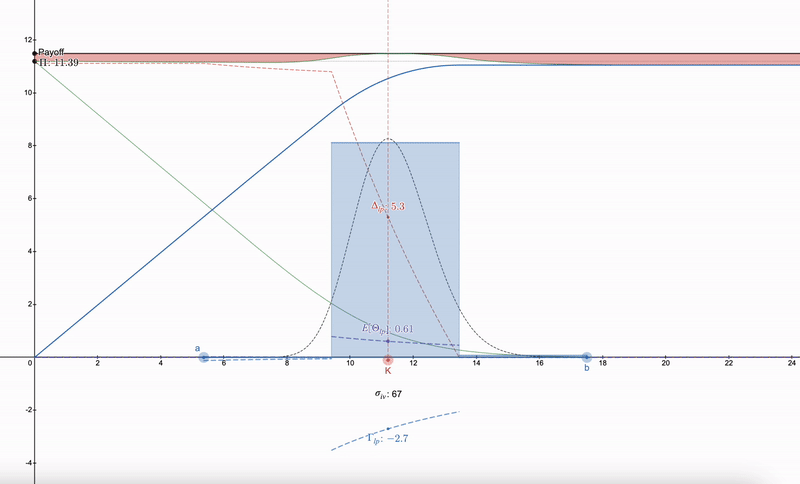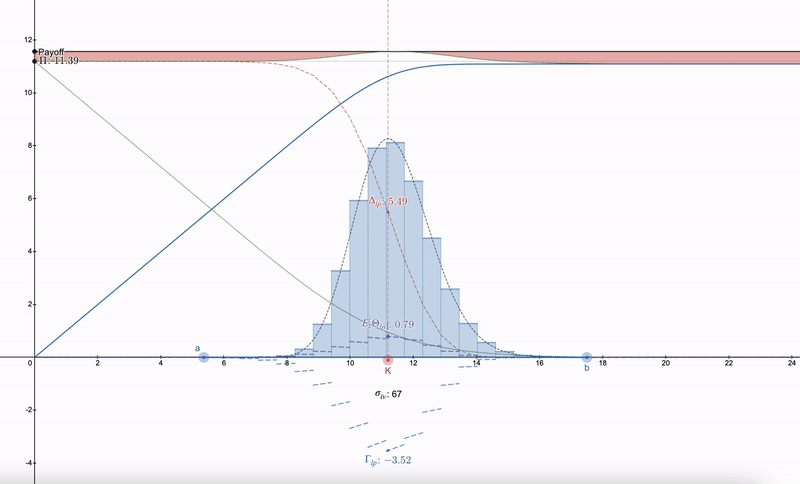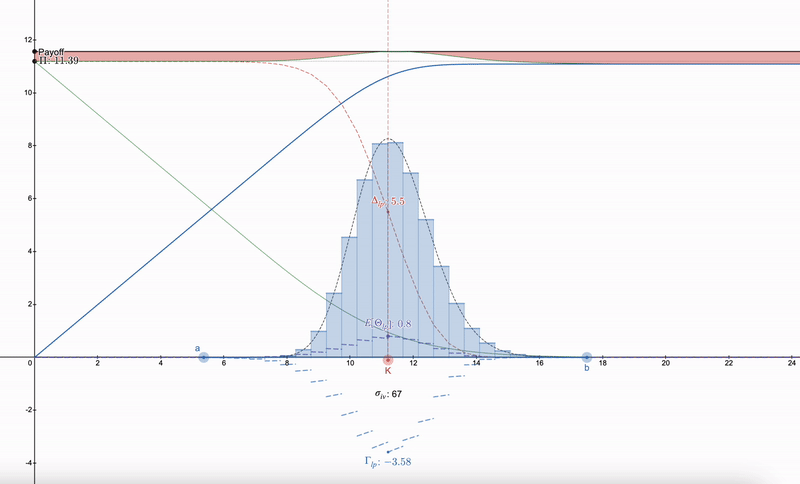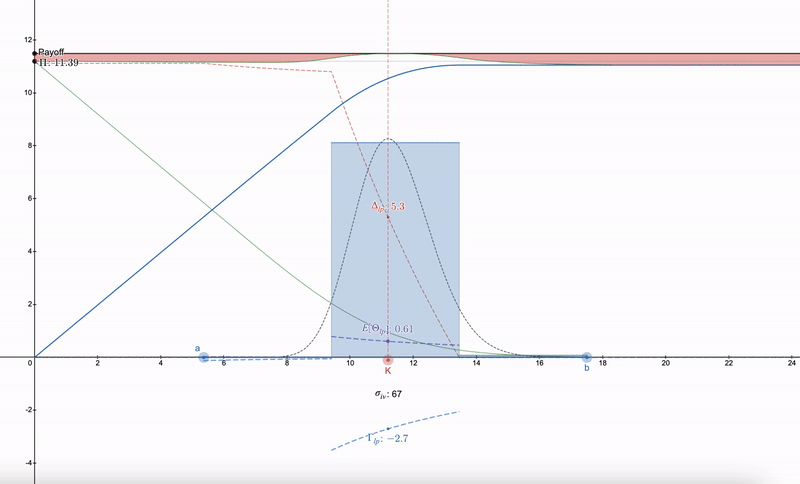
LP 그리스 매개변수는 옵션과 유사하게 시작된다는 점에 유의하십시오. 가격이 하락함에 따라 LP 포지션의 다양성은 사람들이 다음 범위로 전환할 수 있게 합니다. 7개 이상의 LP 포지션은 수익의 감소를 가져옵니다.

흥미롭게도, 로그 정규 분포를 사용하여 100% 지불을 취소하는 것은 매우 어렵습니다(내가 틀렸다면 수정해 주세요). 그러나 로그 정규 유동성 지문이 Dirac Delta 함수에 접근하면 위의 차이(위 그림에서 빨간색으로 시각화됨)는 사라집니다. 예를 들어, 아시아 옵션은 정확히 로그 정규 분포를 따르지만, 가격에 더 민감하다는 점이 놀랍습니다. 여기서 Δ와 Γ는 더욱 날카롭습니다. 아시아 옵션의 변동성은 일반 옵션의 1/√3이므로 지불 차이에 미치는 영향이 적습니다:

유럽식 풋 옵션을 사용하여 LP 포지션 조합을 헤지하여 그에 상응하는 아시아 풋 옵션으로 헤지합니다.

하나의 LP 포지션은 대략 유럽 옵션과 일치할 수 있지만, 부드러운 그리스 매개변수를 무시하고, 일련의 LP 포지션은 그리스 문자를 부드럽게 하지만 언덕을 남깁니다. 이러한 균형은 미래에 잠재적인 조정 / 기울어진 유동성 지문을 통해 개선될 수 있습니다.

LP 헤지 전략

반면에, 만약 누군가가 오목한 LP 지불을 취소하려고 하지 않는다면, desmos 파일: https://www.desmos.com/calculator/khvbqzncg9. 다양한 지불 방식의 작동 방식을 확인하는 데 사용할 수 있습니다. 아래는 발생할 수 있는 일련의 지불 예시입니다.

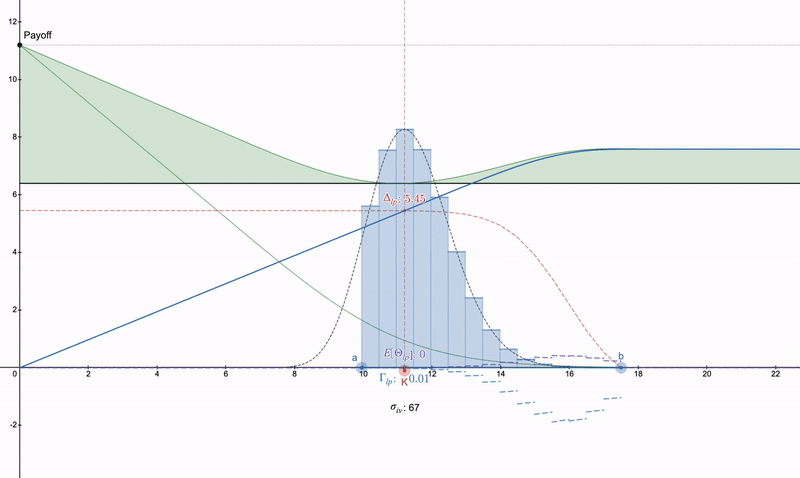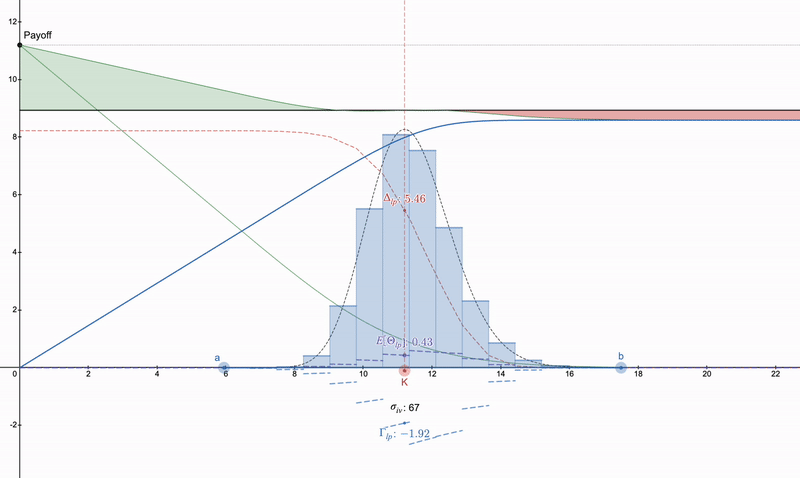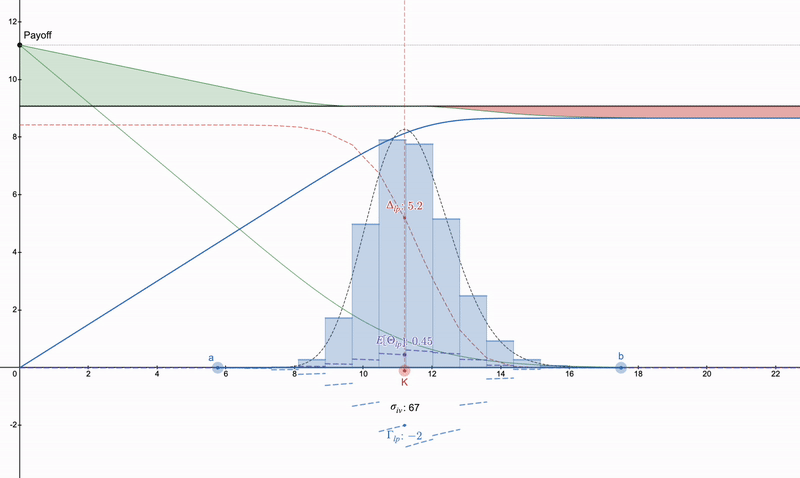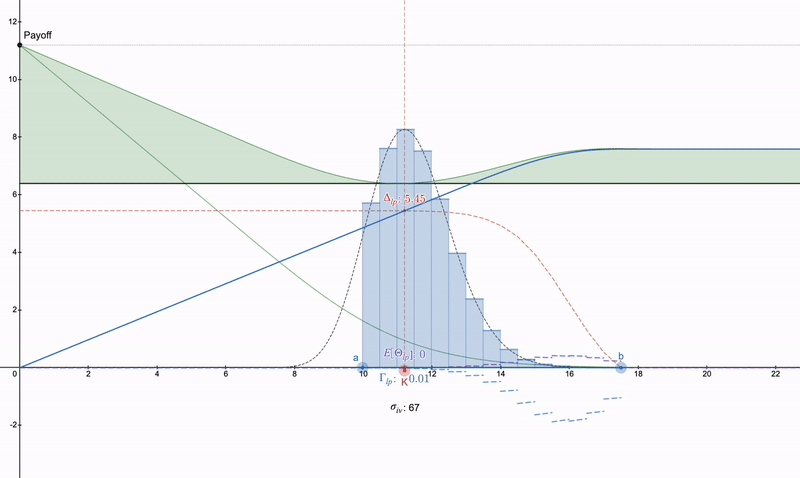
수직 풋 스프레드 >> 풋 옵션 >> 어떤 형태의 롱 스트래들. 세타 감소로 인해 풋 옵션은 시간이 지남에 따라 심화되며, LP 포지션은 비용으로 인해 증가할 수 있습니다.

나는 v3의 흥미로운 특성이 pa의 유동성을 현재 가격의 정확히 75% 또는 그 이하로 집중시키고 pb를 현재 가격으로 설정하면 X 자산의 가치가 25%에서 정점에 이른다는 점을 주목했습니다. 이는 자산을 축적하려는 사람들에게 전략적 가치가 있을 수 있습니다.

Dan Robinson의 v3 도구: https://twitter.com/danrobinson/status/1430678225945042945

이러한 단일 범위를 시장 풋 옵션과 결합하여 다음과 같은 지불을 얻을 수 있습니다: https://www.desmos.com/calculator/a8y3pl3t03:

시장에서 풋 옵션 매개변수를 추출할 수 있습니다. 시간이 지남에 따라 가격이 충분히 빠르게 하락하지 않으면 옵션의 가치는 하락할 것입니다.

이러한 전략은 본질적으로 가격 하락을 추구하여 미래에 자산을 축적하고 수수료를 얻기 위한 것입니다. 주의해야 할 점은 옵션이 없다면 이는 더 위험한 방법이 되며, 실행자가 자산 반등에 대해 매우 확고한 신념을 가질 때만 의미가 있습니다. 그러나 이는 어떤 재정적 조언을 구성하지 않으며, 나는 단지 수학적 계산을 하고 있습니다.

역사적 깊이 파고들기 LVR을 초래하는 원인:

4부에서 나는 LP 포지션의 오목성과 수익 간의 관계를 지적했으며, 역사와 LP 발산 손실 / 손실과 재조정(LVR)의 관점에서 이를 확장하고자 합니다.

Taleb은 위험과 수익의 비선형 관계를 처음으로 기술한 사람은 Louis Bachelier ^[2]^이며, 1900년의 Theory de la Speculation ^[3]^에서 Fourier의 열 방정식과의 유사성에 기인한다고 언급했습니다. 우연히도, Lambert는 Feynman-Kac 방법을 사용하여 집중된 LP 포지션의 가치를 해결했습니다 ^[4]^.

「Theory de la Speculation」의 46페이지. 상수가 제곱되고, dt와 dx²가 있습니다!

Bachelier의 방정식은 약간 재배열된 Black-Scholes-Merton 방정식으로, 드리프트 비율이 0으로 설정됩니다 ^[5]^.

자산 가격의 시간에 따른 변화는 변동성과 곡률과 관련이 있습니다.

LHS는 세타-Θ, RHS는 곡률 감마 Γ이며, 음수 기호로 인해 오목합니다. 그런 다음, 제로 Angeris, Evans 및 Chitra ^[6]^는 AMM의 LP 포지션은 오목한 지불 함수를 가져야 한다고 지적합니다. Curve의 CSMM ^[7]^에서 Forgy＆Lau ^[8]^의 전체 대칭 유동성 곡선 공간에 이르기까지 모든 LP는 오목해야 합니다.

우측 방정식의 오목성에 따라, 이는 시장 조성자(LP) 포지션 자체가 프리미엄을 가져야 함을 의미합니다. 프리미엄이 없으면 아래의 평등이 위반되며, 간단히 이러한 LP 포지션을 차입하고 일부 기초 자산을 매수하여 영구 롱 스트래들 거래를 구축하고 변동성 증가를 활용할 수 있습니다.

Bachelier 등가 / BSM 동적 헤지 - 오목한 명령 수익으로 불리며, 볼록성 명령 비용으로 불립니다. 수학적 표현:

수익 ∝ 위험 곱하기 오목성(음의 볼록성). 부록의 BK 유도.

Uniswap의 Theta 그리스 값을 구하는 과정에서 ^[9]^, LP 포지션의 2차 도함수를 위의 공식에 대입하면 LVR과 동일한 방정식을 얻을 수 있습니다 ^[10]^.

공식 16. Bachelier 등가에서 감마가 -L/2sqrt(x)³이면 동일한 결과를 얻습니다.

LVR 논문 그림 2는 위의 불변 xy=k 그림에서 vol²/8 LVR 관계를 유도하며, 이는 오목한 LP 수익을 초래합니다.

이는 우연이 아니며, 서로 다른 관점에서 동일한 결론을 도출한 사람들입니다. Lambert는 실제로 드리프트 비율을 포함했습니다 ^[11]^, 반면 다른 사람들은 이를 제외했습니다 ^[12]^.

모든 이러한 모델은 가우시안 분포를 가정하며, 이는 이토의 보조정리에서의 브라운 운동(BM) ^[13]^에서 유래하여 내부의 -σ²/2 항을 제공합니다. 이 항은 Angeris, Evans 및 Chitra의 최종 방정식에서도 나타납니다 ^[6]^. 그러나 우리는 디지털 자산, 특히 스테이블코인이 Hurst 지수가 >0.5임을 보여주며, 프랙탈 BM 행동을 암시합니다 ^[14]^. Sepp와 Rakhmonov는 또한 랜덤 변동성 방법이 디지털 자산의 기울어진 암묵적 변동성 구조에 적합하다고 지적했습니다 ^[15]^.

가장 지속적인 디지털 자산의 로그 - 로그 히스토그램의 꼬리 수익을 검토함으로써 우리는 비가우시안 꼬리를 보았습니다.

BTC-USD 히스토그램 수익의 핵 밀도 평활화는 파란색으로 표시됩니다

히스토그램의 형태를 고려할 때, 우리는 Uniswap v2의 전체 범위 균일 분포를 깊이 연구하고 가우시안 절벽을 넘어 시장 조성자에게 적합한 레버리지(LVR) 세타 값을 이해해야 합니다.

50+ 분포의 로그 - 로그 히스토그램. 지수 법칙과 멱 법칙이 심연에서 우리를 기다리고 있습니다.

부록:

Bachelier 등가 유도.

Bachelier 등가에서 유도된 Uniswap LP 포지션의 LVR.

참고 자료:

https://www.desmos.com/calculator/l1oivvaptt

https://www.maths.usyd.edu.au/u/UG/SM/MATH3075/r/HaugTaleb2010.pdf

https://en.wikipedia.org/wiki/LouisBachelier#CITEREFBachelier1900a https://lambert-guillaume.medium.com/pricing-uniswap-v3-lp-positions-towards-a-new-options-paradigm-dce3e3b50125 https://en.wikipedia.org/wiki/Black%E2%80%93Scholesequation https://arxiv.org/abs/2103.14769 https://classic.curve.fi/files/stableswap-paper.pdf https://arxiv.org/pdf/2111.08115.pdf https://www.desmos.com/calculator/fg8a730ddz https://arxiv.org/pdf/2208.06046.pdf https://lambert-guillaume.medium.com/an-analysis-of-the-expected-value-of-the-impermanent-loss-in-uniswap-bfbfebbefed2 https://twitter.com/odtorson/status/1603337199465865216?s=46\&t=e0EQ5vcjHihnkeZ26T4eA https://en.wikipedia.org/wiki/It%C3%B4%27slemma#GeometricBrownianmotion https://scholar.google.com/scholar?q=modelling+multifractal+properties+of+cryptocurrency+markets\&hl=en\&assdt=0\&asvis=1\&oi=scholart https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2810768