Vitalik：用于钱包和其他用例的跨 L2 读取

原文：Deeper dive on cross-L2 reading for wallets and other use cases

作者：Vitalik Buterin

编译：Lynn，MarsBit

 

在《三个转变》一文中，我概述了一些关键原因，说明了将L1 + 跨L2支持、钱包安全和隐私作为生态系统堆栈的必要基本功能来思考的价值，而不是将这些功能作为可以由各个钱包单独设计的附加组件来构建。

本文将更直接地关注一个具体子问题的技术方面：如何更容易地从L2读取L1，从L1读取L2，或者从一个L2读取另一个L2。解决这个问题对于实施资产/密钥库分离架构至关重要，但它在其他领域也有宝贵的用途，尤其是优化可靠的跨L2调用，包括在L1和L2之间移动资产的用例。

 

推荐预先阅读的内容

 

Post on the Three Transitions

Ideas from the Safe team on holding assets across multiple chains

Why we need wide adoption of social recovery wallets

ZK-SNARKs, and some privacy applications

Dankrad on KZG commitments

Verkle trees

 

目录

• 目标是什么？
• 跨链证明是什么样子的？
• 我们可以使用哪些类型的证明方案？
  • 默克尔证明
  • ZK SNARKs
  • 特殊目的的KZG证明
  • Verkle树证明
  • 聚合
  • 直接读取状态
• L2如何学习最近的Ethereum状态根？

• 不属于L2的链上的钱包

• 保护隐私

• 总结

 

目标是什么？

 

一旦L2成为主流，用户将在多个L2和可能的L1上拥有资产。一旦智能合约钱包（多签名、社交恢复或其他方式）成为主流，访问某个账户所需的密钥将会随时间改变，旧密钥将不再有效。一旦这两件事发生，用户将需要一种方式来更改具有访问许多不同地方的多个账户权限的密钥，而不需要进行极高数量的交易。

特别是，我们需要一种处理假设地址的方式：这些地址尚未在区块链上以任何方式“注册”，但仍然需要接收和安全保管资金。我们都依赖于假设地址：当您第一次使用以太坊时，您可以生成一个ETH地址，他人可以用来支付给您，而无需在区块链上“注册”该地址（这将需要支付交易费用，因此需要持有一些ETH）。

对于EOA（外部拥有的账户），所有地址都从假设地址开始。对于智能合约钱包，假设地址仍然是可能的，这在很大程度上要归功于CREATE2，它允许您拥有一个ETH地址，只能由具有与特定哈希匹配的代码的智能合约填充。

EIP-1014（CREATE2）地址计算算法

然而，智能合约钱包引入了一个新的挑战：访问密钥可能会发生变化。地址是initcode的哈希值，只能包含钱包的初始验证密钥。当前的验证密钥将存储在钱包的存储中，但这个存储记录不会自动传播到其他L2链上。

如果用户在许多L2链上有许多地址，包括那些（因为它们是虚拟的）所在的L2链不知道的地址，那么似乎只有一种方法可以让用户更改他们的密钥：资产/密钥存储分离架构。每个用户都有（i）一个“密钥存储合约”（在L1或特定的L2链上），它存储了所有钱包的验证密钥以及更改密钥的规则，以及（ii）在L1和许多L2链上的“钱包合约”，它们通过跨链读取来获取验证密钥。

 

有两种实现方式：

轻量级版本（仅检查更新密钥）：每个钱包在本地存储验证密钥，并包含一个可调用的函数来检查密钥库当前状态的跨链证明，并更新本地存储的验证密钥以匹配。当某个 L2 上首次使用钱包时，调用该函数从密钥库获取当前的验证密钥是必需的。

优点：非常节约使用跨链证明，因此跨链证明昂贵也没关系。所有资金只能使用当前的密钥，因此仍然安全。

缺点：要更改验证密钥，必须在密钥库和已初始化的每个钱包（虽然不包括虚拟钱包）上进行链上密钥更改。这可能会消耗很多 Gas。

重型版本（每个交易都检查）：每个交易都需要一个显示密钥库当前密钥的跨链证明。

优点：系统复杂性较低，且快速更新密钥库。

缺点：每个交易都很昂贵，因此需要更多的工程来使跨链证明价格合理。同时不容易与当前不支持验证期间对可变对象进行跨合约读取的 ERC-4337 兼容。

 

跨链证明是什么样子的？

 

为了展示完整的复杂性，我们将探讨最困难的情况：密钥库位于一个L2上，而钱包位于另一个L2上。如果密钥库或钱包位于L1上，则只需要这个设计的一半。

 

假设密钥库位于Linea，钱包位于Kakarot。完整证明钱包密钥的过程包括：

• 提供当前Linea状态根的证明，给定Kakarot所知道的当前以太坊状态根。
• 提供当前密钥库中密钥的证明，给定当前Linea状态根。

这里有两个主要的实现难题：

我们使用什么样的证明？（是Merkle证明吗？还是其他的什么？）

L2如何首先了解最新的L1（以太坊）状态根（或者，我们将看到，潜在的完整L1状态）？而且，L1如何了解L2状态根？

在这两种情况下，一方发生某事后，到另一方能够提供证明之间会有多长的延迟时间？

 

我们可以使用哪些种类的证明方案？

 

有五个主要选择：

• Merkle证明
• 通用ZK-SNARKs
• 特殊目的证明（例如，使用KZG）
• Verkle证明，介于KZG和ZK-SNARKs之间，既考虑基础设施工作量又考虑成本。
• 没有证明，依赖直接状态读取

就所需的基础设施工作和用户成本而言，我大致将它们排列如下：

“聚合”是指将每个区块中用户提供的所有证明聚合成一个大的元证明，将它们合并在一起。这对于SNARKs和KZG是可行的，但对于Merkle分支来说不行（你可以稍微合并Merkle分支，但实际上只能节省log(txs per block) / log(total number of keystores)，大约15-30% ，所以可能不值得成本）。

聚合只在方案具有大量用户时才变得有价值，因此从实际角度考虑，版本1的实施可以不考虑聚合，在版本2中实施。

 

默克尔证明如何工作？

 

这个很简单：直接按照前一节的图表操作。更具体地说，每个“证明”（假设在证明一个L2进入另一个L2的最困难情况下）包含以下内容：

一个Merkle分支，证明了持有L2键库的状态根，根据L2所知道的以太坊的最新状态根。持有L2键库的状态根存储在已知地址（代表L2的L1合约）的已知存储槽中，因此可以将路径硬编码。

一个Merkle分支，证明了当前的验证密钥，根据持有L2键库的状态根。同样，验证密钥存储在已知地址的已知存储槽中，因此路径可以硬编码。

不幸的是，以太坊的状态证明很复杂，但是有一些库可以用来验证它们，如果使用这些库，这个机制并不太复杂。

更大的问题是成本。默克尔证明很长，而且帕特里夏树的长度比理论上需要的长度长大约3.9倍（确切地说：一个理想的将N个对象存储在树中的Merkle证明长度为32 * log2(N)字节，由于以太坊的帕特里夏树每个子节点有16个叶子节点，针对这些树的证明长度约为32 * 15 * log16(N) ~= 125 * log2(N)字节）。在大约2.5亿个（2²⁸）账户的状态下，每个证明的大小为125 * 28 = 3500字节，约为56,000 gas，再加上解码和验证哈希的额外成本。

两个证明加在一起大约会耗费100,000到150,000 gas（不包括每个交易使用的签名验证），远远超过当前每个交易的基本21000 gas。但是，如果在L2上验证证明，不平等现象会加剧。L2内部的计算较便宜，因为它在链下进行，并且节点数量比L1少得多。然而，数据必须发送到L1。因此，比较不是21000 gas与150,000 gas；而是21000个L2 gas与100,000个L1 gas。

我们可以通过比较L1 gas成本和L2 gas成本来计算出这意味着什么。

以太坊 L1 和 L2 Gas 比较

目前，简单的发送操作，在L1网络上的成本大约是L2的15-25倍，而令牌交换的成本则大约是L2的20-50倍。简单的发送操作相对而言数据量较大，而交换操作则在计算上更加重负。因此，交换操作是一个更好的基准来近似L1计算与L2计算的成本。综合考虑以上情况，如果我们假设L1计算成本和L2计算成本之间的成本比为30倍，这似乎意味着将Merkle证明放在L2上的成本可能相当于大约五十个常规交易。

当然，使用二进制Merkle树可以减少成本约为4倍，但即使如此，在大多数情况下，成本仍然会过高 - 而且如果我们愿意放弃与以太坊当前的六进制状态树的兼容性，我们可能会寻求更好的选择。

 

ZK-SNARK证明如何工作？

 

从概念上看，使用ZK-SNARKs也很容易理解：你只需用证明这些Merkle证明存在的ZK-SNARK来替代上图中的Merkle证明。一个ZK-SNARK的计算成本大约为约400,000个gas，大小约为400个字节（相比之下，未来基本交易的计算成本为21,000个gas和100个字节，压缩后可能减少至约25个字节）。因此，从计算的角度来看，一个ZK-SNARK的成本是一个基本交易的19倍，从数据的角度来看，一个ZK-SNARK的成本是一个基本交易的4倍，未来可能是一个基本交易成本的16倍。

这些数字相比Merkle证明有了巨大的改进，但仍然非常昂贵。有两种方法可以改进这一点：（i）特定用途的KZG证明，或者（ii）聚合，类似于ERC-4337聚合，但使用更高级的数学。我们可以研究这两种方法。

 

专用KZG证明如何工作？

 

警告，本节内容比其他部分更加数学化。这是因为我们要超越通用工具，构建一些特殊用途的更便宜的工具，所以我们需要更深入地了解。如果你不喜欢深入的数学知识，可以直接跳到下一节。

首先，回顾一下KZG承诺的工作原理：

• We can represent a set of data [D_1 ... D_n] with a KZG proof of a polynomial derived from the data: specifically, the polynomial P where P(w) = D_1, P(w²) = D_2 ... P(wⁿ) = D_n. w here is a "root of unity", a value where wᴺ = 1 for some evaluation domain size N (this is all done in a finite field).
• To "commit" to P, we create an elliptic curve point com(P) = P₀ * G + P₁ * S₁ + ... + Pₖ * Sₖ. Here:
• G is the generator point of the curve
• Pᵢ is the i'th-degree coefficient of the polynomial P
• Sᵢ is the i'th point in the trusted setup
• To prove P(z) = a, we create a quotient polynomial Q = (P - a) / (X - z), and create a commitment com(Q) to it. It is only possible to create such a polynomial if P(z) actually equals a.
• To verify a proof, we check the equation Q * (X - z) = P - a by doing an elliptic curve check on the proof com(Q) and the polynomial commitment com(P): we check e(com(Q), com(X - z)) ?= e(com(P) - com(a), com(1))

一些重要的关键属性需要理解：

• A proof is just the com(Q) value, which is 48 bytes
• com(P₁) + com(P₂) = com(P₁ + P₂)
• This also means that you can "edit" a value into an existing a commitment. Suppose that we know that D_i is currently a, we want to set it to b, and the existing commitment to D is com(P). A commitment to "P, but with P(wⁱ) = b, and no other evaluations changed", then we set com(new_P) = com(P) + (b-a) * com(Lᵢ), where Lᵢ is a the "Lagrange polynomial" that equals 1 at wⁱ and 0 at other wʲ points.
• To perform these updates efficiently, all N commitments to Lagrange polynomials (com(Lᵢ)) can be pre-calculated and stored by each client. Inside a contract on-chain it may be too much to store all N commitments, so instead you could make a KZG commitment to the set of com(L_i) (or hash(com(L_i)) values, so whenever someone needs to update the tree on-chain they can simply provide the appropriate com(L_i) with a proof of its correctness.

因此，我们拥有一个结构，我们可以不断向一个不断增长的列表的末尾添加值，尽管有一定的大小限制（实际上，数亿个值是可行的）。然后，我们将其作为我们的数据结构来管理（i）存储在L2上并镜像到L1的键列表的承诺，以及（ii）存储在以太坊L1上并镜像到每个L2的L2键承诺列表的承诺。

保持承诺的更新可以成为核心L2逻辑的一部分，或者可以通过存款和提款桥实现而不需要L2核心协议的更改。

一份完整的证明所需的内容如下：

1. 存放L2上密钥库的最新com（密钥列表）（48字节）

2. 将com（密钥列表）作为com（镜像列表）中的值的KZG证明，com（镜像列表）是所有密钥列表承诺的列表（48字节）

3. 将您的密钥在com（密钥列表）中的KZG证明（48字节，加上4字节的索引）

实际上可以将这两个KZG证明合并为一个，因此总大小只有100字节。

请注意一个细节：由于密钥列表是一个列表，而不是像状态那样的键/值映射，密钥列表必须按顺序分配位置。密钥承诺合约将包含其自己的内部注册表，将每个密钥库映射到一个ID，并且对于每个密钥，它将存储hash（key，密钥库的地址）而不仅仅是key，以明确地告知其他L2关于特定条目所指的密钥库。

这种技术的优点是在L2上性能非常好。数据只有100字节，比ZK-SNARK短约4倍，比Merkle证明短得多。计算成本主要是一个大小2的对检查，大约为119,000 gas。在L1上，计算比数据更重要，所以不幸的是，KZG比Merkle证明要稍微昂贵一些。

 

Verkle 树如何工作？

 

Verkle树是什么样子。在实践中，对于基于IPA的树，可以给每个节点一个宽度为256 == 2⁸，或者对于基于KZG的树，宽度为2²⁴

Verkle树中的证明比KZG要长一些；它们可能会有几百个字节长。它们也很难验证，特别是当你试图将许多证明合并成一个时。

从实际角度来看，Verkle树应该被认为是类似于Merkle树，但在没有SNARK的情况下更可行（因为数据成本较低），而在使用SNARK的情况下更便宜（因为证明成本较低）。

Verkle树的最大优势是可能实现数据结构的协调：Verkle证明可以直接在L1或L2状态上使用，无需叠加结构，并且对于L1和L2使用完全相同的机制。一旦量子计算机成为问题，或者一旦证明Merkle分支变得足够高效，Verkle树可以被适当的SNARK友好哈希函数替换为二进制哈希树。

 

聚合

 

如果N个用户做了N笔交易（或者更现实的说，N个ERC-4337 UserOperations），需要证明N个跨链索赔，我们可以通过聚合这些证明来节省大量的气体：将这些交易合并到一个区块或捆绑到一个区块的构建者可以创建一个单一的证明，同时证明所有这些索赔。

这可能意味着：

• 一个N个Merkle分支的ZK-SNARK证明
• 一个KZG多重证明
• 一个Verkle多重证明（或一个多重证明的ZK-SNARK）

在所有这三种情况下，每个证明只需花费几十万气体。建设者需要在每个L2上为该L2的用户制作一个这样的证明；因此，为了使这个证明有用，整个计划需要有足够的使用量，以至于在多个主要L2的同一区块内经常有至少几个交易。

如果使用ZK-SNARKs，主要的边际成本只是在合同之间传递数字的 "商业逻辑"，因此每个用户可能有几千个L2气体。如果使用KZG多重证明，验证者需要为该区块内使用的每个持有钥匙库的L2增加48个气体，所以每个用户的方案的边际成本将在此基础上再增加每个L2（不是每个用户）的~800个L1气体。但这些成本比不聚合的成本要低得多，后者不可避免地涉及到每个用户超过10000个L1气体和数十万个L2气体。对于Verkle树，你可以直接使用Verkle多证明，每个用户增加大约100-200字节，或者你可以做一个Verkle多证明的ZK-SNARK，它的成本与Merkle分支的ZK-SNARK相似，但证明起来明显便宜。

从实施的角度来看，让捆绑者通过ERC-4337账户抽象标准聚合跨链证明可能是最好的。ERC-4337已经有一个机制，让构建者以自定义的方式聚合UserOperations的部分。甚至有一个针对BLS签名聚合的实现，这可以将L2的气体成本降低1.5倍到3倍，这取决于包括哪些其他形式的压缩。

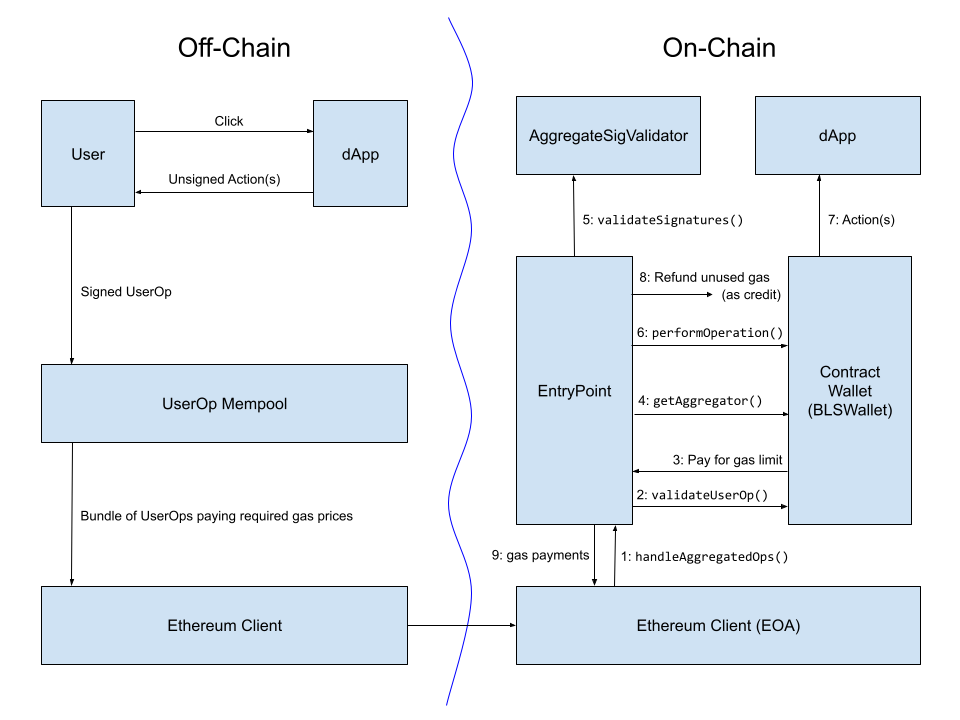
来自BLS钱包实现帖子的图表，显示了在ERC-4337的早期版本中BLS聚合签名的工作流程。聚合跨链证明的工作流程可能看起来非常相似

 

直接读取状态

 

最后一种可能，也是只适用于L2读L1（而不是L1读L2）的一种可能，就是修改L2，让它们直接对L1的合约进行静态调用。

这可以通过一个操作码或预编译来实现，它允许调用L1，你提供目标地址、气体和calldata，然后它返回输出，尽管由于这些调用是静态调用，它们实际上不能改变任何L1状态。L2必须知道L1的情况才能处理存款，所以没有什么根本性的东西可以阻止这种东西的实现；这主要是一个技术实现上的挑战（见：Optimism的这个RFP支持静态调用到L1）。

请注意，如果钥匙库在L1上，并且L2整合了L1的静态调用功能，那么就根本不需要证明！但是，如果L2不在L1上，那么就不需要证明！然而，如果L2没有整合L1静态调用，或者如果钥匙库在L2上（它最终可能必须在L2上，一旦L1变得太贵，用户甚至无法使用一点点），那么就需要证明了。

 

L2如何学习最近的Ethereum状态根？

 

上述所有的方案都要求L2访问最近的L1状态根，或者整个最近的L1状态。幸运的是，所有的L2都有一些功能来访问最近的L1状态。这是因为它们需要这样的功能来处理从L1到L2的消息，最明显的是存款。

事实上，如果L2有一个存款功能，那么你就可以按原样使用L2来把L1的状态根移到L2的合约中：只要让L1的合约调用BLOCKHASH操作码，并把它作为一个存款消息传递给L2。完整的块头可以被接收，它的状态根也可以在L2端被提取出来。然而，对于每个L2来说，最好是有一个明确的方法来直接访问完整的最近的L1状态，或者最近的L1状态根部。

优化L2接收最近L1状态根的方式的主要挑战是同时实现安全和低延时：

• 如果L2以一种懒惰的方式实现 "直接读取L1 "的功能，只读取最终确定的L1状态根，那么延迟通常为15分钟，但在非活动泄漏的极端情况下（你必须容忍），延迟可能是几个星期。
• L2绝对可以被设计成读取更近的L1状态根，但是因为L1可以恢复（即使是单槽的最终状态，恢复也可能发生在非活动性泄漏期间），L2也需要能够恢复。从软件工程的角度来看，这在技术上具有挑战性，但至少Optimism已经有这个能力。
• 如果你使用存款桥将L1状态的根带入L2，那么简单的经济可行性可能需要在存款更新之间有很长的时间：如果存款的全部成本是10万gas，我们假设ETH是1800美元，费用是200gwei，L1的根每天被带入L2一次，这将是每个L2每天36美元的成本，或者每个L2每年13148美元来维护系统。如果延迟一小时，那就上升到每年每个L2 315,569美元。在最好的情况下，不耐烦的富裕用户不断涌入，支付更新费用，并为其他人保持系统的更新。在最坏的情况下，一些利他主义的行为者将不得不自己付钱。
• "神谕"（至少，一些定义者称之为 "神谕 "的那种技术）在这里不是一个可接受的解决方案：钱包密钥管理是一个非常安全关键的低级功能，因此它应该最多依赖于几件非常简单的、加密上不可信任的低级基础设施。

此外，在相反的方向（L1s读取L2）：

• 在乐观的滚动中，由于欺诈证明的延迟，国家根基需要一个星期才能达到L1级。在ZK滚动中，由于证明时间和经济限制的结合，目前需要几个小时，尽管未来的技术会减少这一点。
• 预先确认（来自测序者、测试者等）对于L1读L2来说不是一个可接受的解决方案。钱包管理是一个非常安全的低级功能，因此L2->L1通信的安全水平必须是绝对的：甚至不应该通过接管L2验证器集来推送一个虚假的L1状态根。L1唯一应该信任的状态根是被L2对L1的状态根持有合同接受为最终的状态根。

对于许多defi用例来说，这些无信任的跨链操作的一些速度是不可接受的；对于这些用例，你确实需要更快的桥接和更不完善的安全模型。然而，对于更新钱包钥匙的用例，较长的延迟是可以接受的：你不是把交易延迟几个小时，你是在延迟钥匙的变化。你只是要把旧的钥匙保留更长的时间。如果你因为钥匙被盗而更换钥匙，那么你确实有一段相当长的脆弱期，但这是可以缓解的，例如，通过钱包的冻结功能。

最终，最好的延迟最小化解决方案是L2以最佳方式实现对L1状态根的直接读取，其中每个L2块（或状态根计算日志）包含一个指向最近L1块的指针，所以如果L1还原，L2也可以还原。Keystore合约应该放在mainnet上，或者放在L2上，因为L2是ZK-rollups，所以可以快速提交给L1。

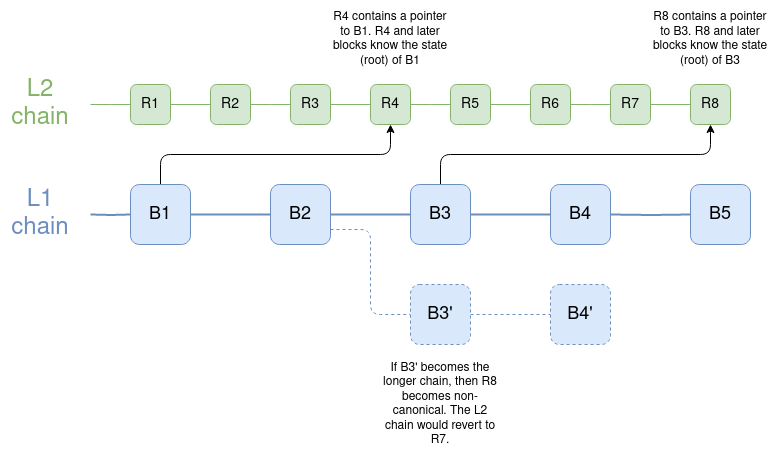
L2链的区块不仅可以对以前的L2区块有依赖性，还可以对L1区块有依赖性。如果L1还原了这样的链接，L2也会还原。值得注意的是，这也是早期（Dank之前）版本的分片设想的工作方式；代码见这里

 

另一条链需要与以太坊有多大的联系，才能持有其密钥库扎根于以太坊或L2的钱包？

 

令人惊讶的是，没有那么多。事实上，它甚至不需要是一个卷轴：如果它是一个L3，或一个validium，那么在那里持有钱包是可以的，只要你在L1或ZK卷轴上持有密钥存储。你需要的是链上的人能够直接访问以太坊的状态根，并且在技术上和社会上承诺愿意在以太坊重构时进行重构，在以太坊硬分叉时进行硬分叉。

一个有趣的研究问题是确定一条链在多大程度上有可能与其他多个链（如以太坊和Zcash）建立这种形式的联系。天真地做是可能的：如果以太坊或Zcash重组，你的链可以同意重组（如果以太坊或Zcash硬分叉，则硬分叉），但这样你的节点操作员和你的社区更普遍地有双重的技术和政治依赖。因此，这样的技术可以用来连接到其他一些链上，但成本会越来越高。基于ZK桥的方案有吸引人的技术特性，但它们有一个关键的弱点，即它们对51%的攻击或硬分叉不健全。可能有更巧妙的解决方案。

 

保护隐私

 

理想情况下，我们也希望保护隐私。如果你有许多钱包是由同一个密钥库管理的，那么我们要确保：

• 不让公众知道这些钱包都是相互连接的。
• 社会恢复监护人不会了解他们所监护的地址是什么。

这就产生了一些问题：

• 我们不能直接使用Merkle证明，因为它们不能保护隐私。
• 如果我们使用KZG或SNARKs，那么证明需要提供验证密钥的盲文版本，而不透露验证密钥的位置。
• 如果我们使用聚合，那么聚合者就不应该了解明文的位置；相反，聚合者应该收到盲文证明，并有办法聚合这些证明。
• 我们不能使用 "轻型版本"（仅使用跨链证明来更新密钥），因为它产生了隐私泄露：如果许多钱包由于更新程序而同时被更新，那么时间上就会泄露这些钱包可能是相关的信息。所以我们必须使用 "重型版本"（为每笔交易提供跨链证明）。

使用SNARKs，解决方案在概念上很容易：证明默认是信息隐藏的，聚合器需要产生一个递归的SNARK来证明SNARKs。

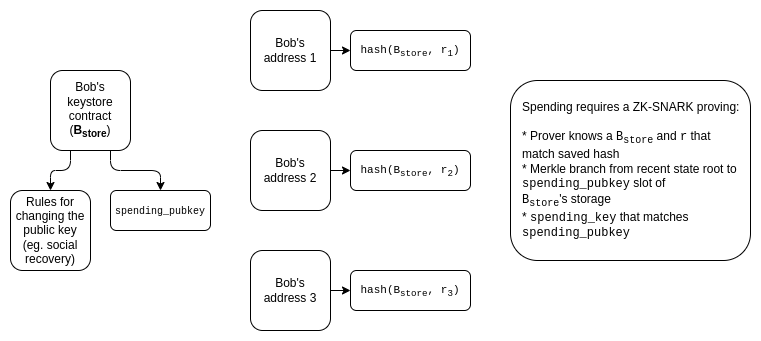
今天这种方法的主要挑战是，聚合需要聚合者创建一个递归的SNARK，这目前是相当慢的。

对于KZG，我们可以用这个关于非索引揭示的KZG证明的工作（另见：Caulk论文中该工作的一个更正式的版本）作为一个起点。然而，盲证的聚合是一个需要更多关注的开放性问题。

不幸的是，直接从L2内部读取L1并不能保护隐私，尽管实现直接读取功能仍然非常有用，这既是为了最大限度地减少延迟，也是因为它对其他应用的效用。

 

总结

 

• 为了拥有跨链的社会恢复钱包，最现实的工作流程是在一个地方维护一个密钥库，而在许多地方的钱包，钱包读取密钥库，要么（i）更新他们对验证密钥的本地视图，要么（ii）在验证每个交易的过程中。
• 实现这一点的一个关键因素是跨链证明。我们需要努力优化这些证明。无论是ZK-SNARKs，等待Verkle证明，还是定制的KZG解决方案，似乎都是最佳选择。
• 从长远来看，聚合协议，即捆绑者生成聚合证明，作为创建用户提交的所有UserOperations的捆绑的一部分，对于最小化成本是必要的。这可能应该被整合到ERC-4337生态系统中，尽管可能需要对ERC-4337进行修改。
• L2应该被优化，以尽量减少从L2内部读取L1状态（或至少是状态根）的延迟。L2s直接读取L1状态是理想的，可以节省证明空间。
• 钱包不仅可以在L2上，你也可以把钱包放在与以太坊连接级别较低的系统上（L3s，甚至单独的链，只同意包括以太坊状态根，并在以太坊重构或硬分叉时重构或硬分叉）。
• 然而，钥匙库应该钥匙库应该在L1或在高安全性的ZK-rollup L2上。在L1上可以节省大量的复杂性，尽管从长远来看，即使是这样也可能太昂贵了，因此需要在L2上建立密钥库。
• 保护隐私将需要额外的工作，并使一些选项更加困难。然而，我们也许应该朝着保护隐私的解决方案前进，至少要确保我们提出的任何方案都是与保护隐私相兼容的。