Uniswap v3 數學洞察：期權如何與頭寸結合

撰文：ck.eth

編譯：Lylia， Antalpha Labs

原系列共有六部分，此為第五部分，該篇繼續介紹期權如何與頭寸結合，需要對該系列之前所述的頭寸策略有一定了解。為了讓更多人可以訪問和了解關於 Uniswap V3 的有用信息，我們翻譯了系列文章，讓中文讀者對 Uniswap v3 機制和投資策略選擇有更深入的理解。在閱讀本翻譯同時，可以隨時參考原文以獲取更多詳細信息。

Uniswap 收益凸性風險的非線性 / Theta-Gamma 波動性。https://www.math3d.org/WvsEXvTWD

簡而言之：

• 展示了對 Uniswap v2 和 v3 的希臘解決方案
• 在交互式 desmos 文件中提供了使用 Uniswapv3 對亞洲期權、歐式期權和 Bachelier 期權進行對沖的解決方案。
• 展示了使用 desmos 對 LP 對沖積累策略。
• 解釋了導致 LVR 的歷史和替代推導。

希臘參數 - Uniswap v2

與其將 100% 分配給 LP 頭寸，不如將部分分配給 X 資產的做法，其餘部分用於做空 X 資產以減少但不消除發散損失。結果是將支付結構從懸崖轉換為山丘，如 Guillaume Lambert 所示：希臘參數告訴人們 LP 頭寸的價值相對於另一變量（例如，時間，波動率和利率）的敏感性。我們在第 4 部分中介紹了 Delta 和 Gamma。LP 希臘參數很有用，因為你可以將它們與期權的希臘參數匹配，以抵消價格分歧，例如，當價格波動、波動率變化或時間流逝時的效應，即 delta 和 gamma。希臘參數的數值告訴我們各種因素對 LP 頭寸價格的影響。

v2 的交互式 desmos 文件：https://www.desmos.com/calculator/inwy6djhhm

需要注意的是，與期權相比，Uniswap 的希臘參數在 LP 頭寸價格下跌時會趨向於無窮，如上圖中在 x=0 處以虛線表示。為了削減這些尾部風險，我們可以使用 v3 中的集中範圍。

希臘參數 - 集中 LP 範圍 v3

univ3 希臘參數的 desmos 文件：https://www.desmos.com/calculator/l8sqzlwkf5

我們將範圍 pa （下限）~pb （上限）集中得越小，我們的 Delta Δ 和 Gamma Γ 就越敏感，注意 Gamma 為負，這意味著我們的 LP 支付具有凹形黑色形狀。我們的 theta /Θ / 預期費用也會增加，而利率敏感度 ρ 基本上不受影響。

但是，雖然單個 LP 頭寸的支付圖可能與期權匹配，但其他希臘參數可能不匹配。

LP 希臘參數看起來不像常規期權：https://www.desmos.com/calculator/nyuw7sybin

在這裡，我們有一個單個 LP 範圍的認購期權，但其他希臘參數並不是固定的。

可以使用的技巧是，與其試圖找到對沖 LP 頭寸的方法，人們首先需要在市場上找到一個具有執行價格（K）以及隱含波動率（σ_iv ）和到期時間（t ）的期權。之後，可以構建一個遵循對數正態分布的一系列 LP 頭寸，最初是受丹·羅賓遜（Dan Robinson）對 Uniswap v3 的正態分布流動性指紋啟發的 ^[1]^。LP 頭寸在價格空間上匹配對數正態分布的粒度化允許對希臘參數進行平滑處理：

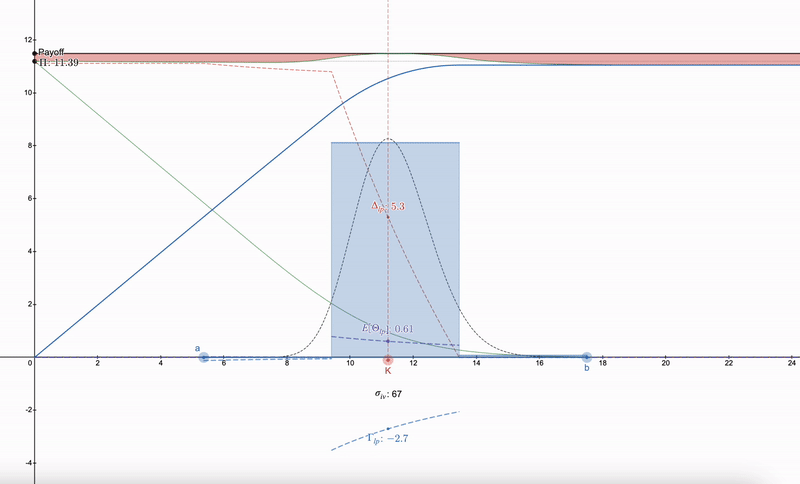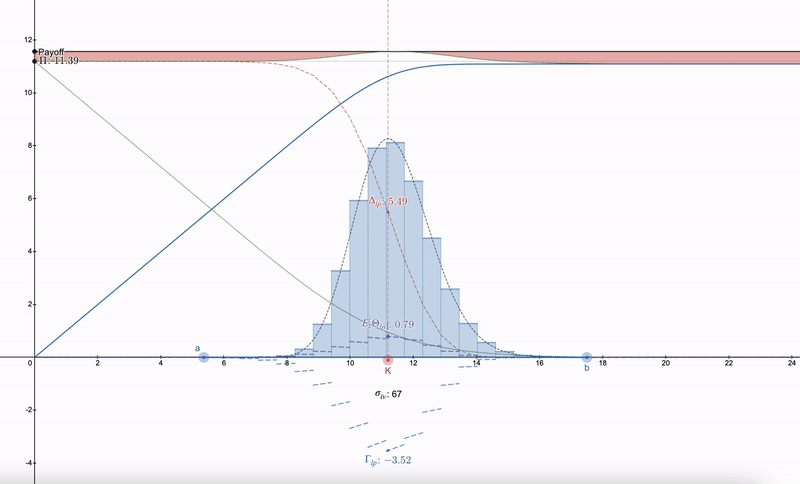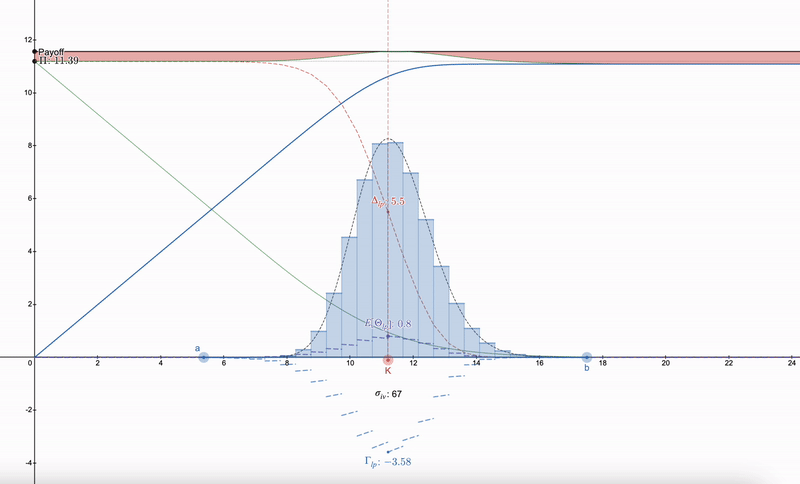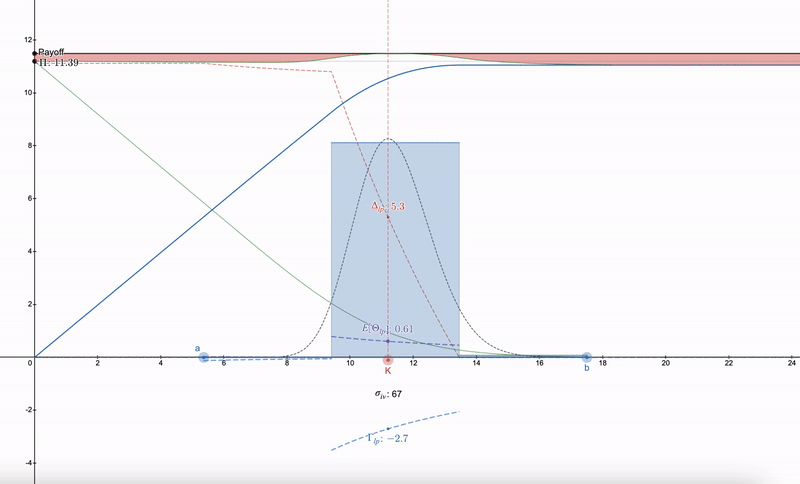
請注意，LP 希臘語開始類似於期權。隨著價格的下降，LP 頭寸的多樣性使人們可以切換到下一個範圍。超過 7 個 LP 頭寸會帶來收益的遞減。

奇怪的是，使用對數正態分布 100％ 取消支付似乎非常困難（如果我錯了，請糾正我），但是如果對數正態流動性指紋逼近 Dirac Delta 函數，則上述差異（上圖中以紅色可視化）會消失。例如，亞洲期權恰好也遵循對數正態分布，但令人意外的是，它對價格更敏感，其中 Δ 和 Γ 更加銳利，因為亞洲期權的波動率為常規期權的 1/√3，因此對支付分歧的影響較小：

使用歐式看跌期權對沖 LP 頭寸組合以使用其等價的亞洲看跌期權進行對沖。

一個 LP 頭寸可以大致匹配歐式期權，但會忽略平滑的希臘參數，而一系列 LP 頭寸會平滑希臘字母卻會留下一個山丘。這種權衡可能在未來通過潛在的調整 / 偏斜流動性指紋得到改善。

LP 對沖策略

另一方面，如果一個人不感興趣嘗試取消凹形 LP 支付，那麼 desmos 文件: https://www.desmos.com/calculator/khvbqzncg9。也可以用於查看各種支付方式的工作原理。下面是可能出現的一系列支付的示例。

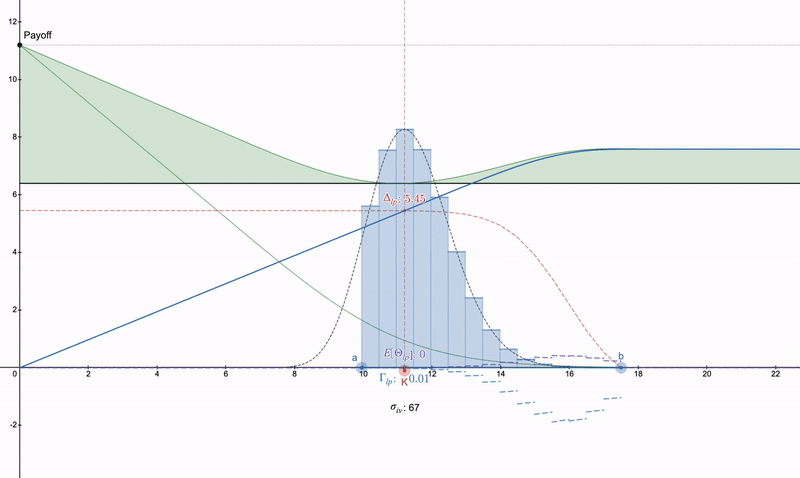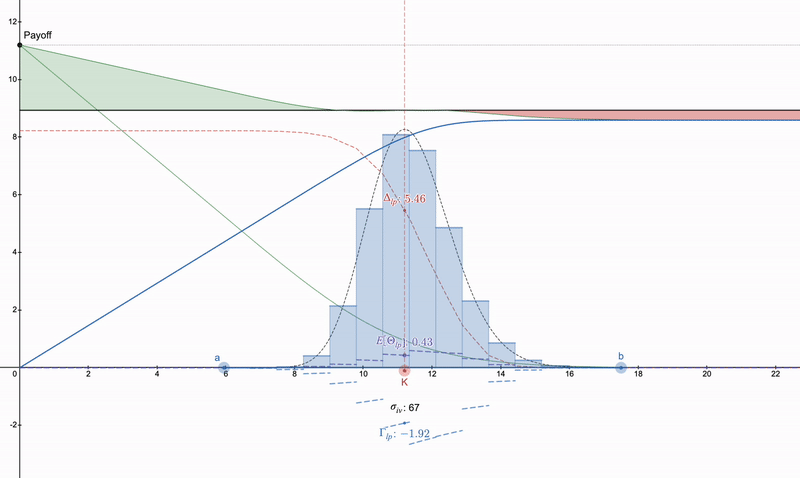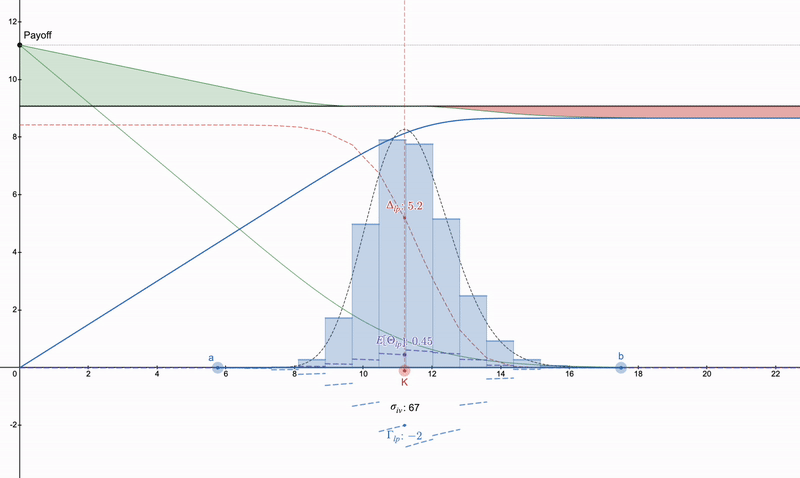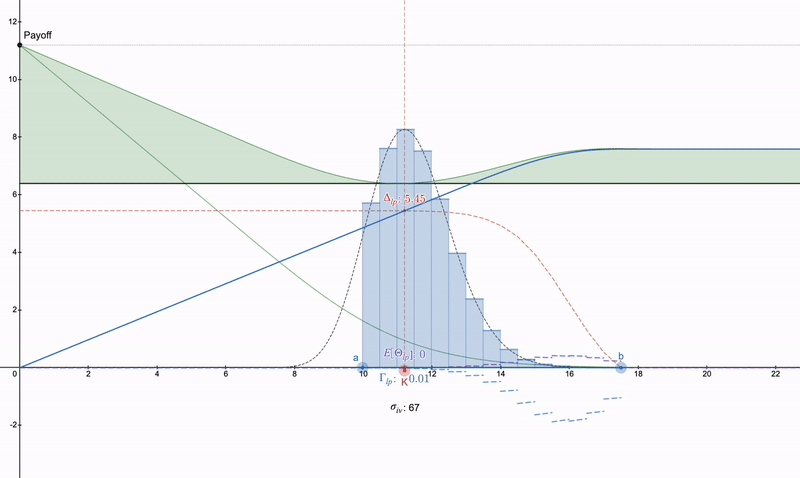
垂直看跌價差>>看跌期權>>某種長跨式。請注意，由於 theta 衰減，看跌期權將隨著時間的推移而加劇，而 LP 頭寸可以由於費用而增長。

我注意到 v3 的一個有趣特性是，如果將 pa 的流動性集中在當前價格的正好 75% 或更低，並將 pb 設為當前價格，那麼 X 資產的價值會在 25% 處達到峰值，這對於試圖積累資產的人可能具有一定的戰略價值。

Dan Robinson 的 v3 工具：https://twitter.com/danrobinson/status/1430678225945042945

可以將這樣的單個範圍與市場看跌期權結合使用，以獲得以下支付：https://www.desmos.com/calculator/a8y3pl3t03：

可以從市場中提取看跌期權參數。隨著時間的推移，如果價格不降低足夠快，期權的價值將下降。

這樣的策略本質上是為了謀求價格下跌以便未來積累資產並賺取費用。需要注意的是，如果沒有期權，這將變成一種更具風險的方法，只有在執行者對資產反彈有非常堅定的信念時才有意義。不過，請注意，這並不構成任何財務建議，我只是在做數學運算。

歷史深入挖掘導致 LVR：

在第 4 部分中，我指出了 LP 頭寸的凹形和收益之間的關係，並希望從歷史和 LP 發散損失 / 損失與再平衡（LVR）的角度加以擴展。

Taleb 指出，第一個寫下風險和回報的非線性關係的人是 Louis Bachelier ^[2]^在 1900 年的 Theory de la Speculation ^[3]^中歸因於它與 Fourier 的熱方程的相似之處。巧合的是，Lambert 使用 Feynman-Kac 的方法來解決集中的 LP 頭寸的價值 ^[4]^。

「Theory de la Speculation」的第 46 頁。一個常數被平方，一個 dt 和一個 dx²！

Bachelier 的方程只是一種略微重新排列的 Black-Scholes-Merton 方程，其中漂移率設置為零 ^[5]^。

資產價格隨時間的變化與波動率和曲率有關。

LHS 是 theta-Θ，RHS 是曲率 gamma Γ，由於負號，它恰好是凹形的。然後，零 Angeris，Evans 和 Chitra ^[6]^ 指出，AMM 的 LP 頭寸必須具有凹形支付函數。從 Curve 的 CSMM ^[7]^ 到 Forgy＆Lau ^[8]^的整個對稱流動性曲線空間，所有 LP 都應該是凹形的。

根據我們右側方程中的凹平等性，這意味著做市商（LP）頭寸本身必須有溢價。如果沒有溢價，下面的平等就會被違反，並且可以通過簡單地借用這樣一個 LP 頭寸並且買入部分標的資產來構建永續多頭跨式交易，並等待波動率的增加來加以利用。

Bachelier 等價 / BSM 動態對沖 - 稱為凹形命令收益，而凸性命令成本。數學表示：

收益 ∝ 風險乘以凹性（負凸性）。附錄中的 BK 推導。

在求解 Uniswap 的 Theta 希臘值 ^[9]^，我注意到通過將 LP 倉位的二階導數代入上述公式，可以得到與 LVR 相同的方程 ^[10]^。

公式 16。如果 Bachelier 等價中的 Gamma 為 -L/2sqrt(x)³，就會得到相同的結果。

LVR 論文圖 2 從上述不變的 xy=k 圖中推導出了 vol²/8 LVR 關係，該圖導致了凹形 LP 收益。

這並非巧合，來自不同角度的人都得出了相同的結論。Lambert 實際上包含了漂移率 ^[11]^，而其他人則將其排除在外 ^[12]^。

請注意，所有這些模型都假設高斯分布，最初源自伊藤引理中的布朗運動（BM） ^[13]^，這使我們得到了內部的 -σ²/2 項，該項也出現在 Angeris、Evans 和 Chitra 的最終方程中 ^[6]^，但我們知道，數字資產，包括穩定幣，表現出 Hurst 指數>0.5，暗示分形 BM 行為 ^[14]^，Sepp 和 Rakhmonov 也指出，隨機波動率方法適用於數字資產的偏斜隱含波動率結構 ^[15]^。

通過審查最持久數字資產的對數 - 對數直方圖的尾端收益，我們還看到了非高斯尾部。

BTC-USD 直方圖收益的核密度平滑顯示為藍色

鑒於直方圖的形狀，我們將不得不深入研究 Uniswap v2 的全範圍均勻分布，並超越 Gaussian cliff，才能深入了解適合做市商的槓桿率（LVR）theta 值。

50+ 分布的對數 - 對數直方圖。指數律和幂律在深淵中等待著我們。

附錄：

Bachelier 等價推導。

從 Bachelier 等價得出的 Uniswap LP 倉位的 LVR。

參考資料：

https://www.desmos.com/calculator/l1oivvaptt

https://www.maths.usyd.edu.au/u/UG/SM/MATH3075/r/HaugTaleb2010.pdf

https://en.wikipedia.org/wiki/LouisBachelier#CITEREFBachelier1900a https://lambert-guillaume.medium.com/pricing-uniswap-v3-lp-positions-towards-a-new-options-paradigm-dce3e3b50125 https://en.wikipedia.org/wiki/Black%E2%80%93Scholesequation https://arxiv.org/abs/2103.14769 https://classic.curve.fi/files/stableswap-paper.pdf https://arxiv.org/pdf/2111.08115.pdf https://www.desmos.com/calculator/fg8a730ddz https://arxiv.org/pdf/2208.06046.pdf https://lambert-guillaume.medium.com/an-analysis-of-the-expected-value-of-the-impermanent-loss-in-uniswap-bfbfebbefed2 https://twitter.com/odtorson/status/1603337199465865216?s=46\&t=e0EQ5vcjHihnkeZ26T4eA https://en.wikipedia.org/wiki/It%C3%B4%27slemma#GeometricBrownianmotion https://scholar.google.com/scholar?q=modelling+multifractal+properties+of+cryptocurrency+markets\&hl=en\&assdt=0\&asvis=1\&oi=scholart https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2810768