Arweave 제 17판 백서 해석 (4): 전체 데이터 복사본 저장이 진리다

해석(삼) 문서에서는 수학적 유도를 통해 #SPoRes의 실행 가능성을 입증했습니다. 문서의 Bob과 Alice는 이 증명 게임에 참여했습니다. 그러면 #Arweave 채굴에서 프로토콜은 이 SPoRes 게임의 수정 버전을 배포했습니다. 채굴 과정에서 프로토콜은 Bob의 역할을 하고, 네트워크의 모든 채굴자는 Alice의 역할을 함께 수행합니다. SPoRes 게임의 각 유효한 증명은 Arweave의 다음 블록을 생성하는 데 사용됩니다. 구체적으로 Arweave 블록의 생성은 다음 매개변수와 관련이 있습니다:

여기서:

BI = Arweave 네트워크의 블록 인덱스 Block Index;

800*np = 각 체크포인트의 각 파티션에서 최대 800개의 해시를 잠금 해제할 수 있으며, np는 채굴자가 저장하는 크기가 3.6 TB인 파티션의 수입니다. 두 값을 곱한 것은 해당 채굴자가 초당 최대 시도할 수 있는 해시 연산 횟수입니다.

d = 네트워크의 난이도입니다.

성공적인 유효 증명은 난이도 값보다 큰 증명이며, 이 난이도 값은 시간이 지남에 따라 조정되어 평균 120초마다 블록이 생성되도록 합니다. 블록 i와 블록 (i+10) 사이의 시간 차이가 t일 때, 이전 난이도 di에서 새로운 난이도 d{i+10}로의 조정은 다음과 같이 계산됩니다:

여기서:

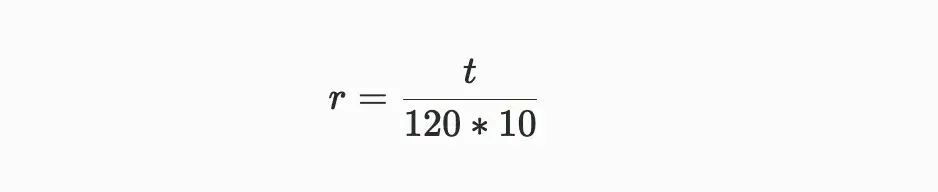
공식 주석: 위의 두 공식에서 볼 수 있듯이, 네트워크 난이도의 조정은 주로 매개변수 r에 의존하며, r은 실제 블록 생성에 필요한 시간이 시스템이 기대하는 120초의 기준 시간에 대한 편차 매개변수를 의미합니다.

새로 계산된 난이도는 생성된 각 SPoA 증명에 기반하여 블록 채굴 성공 확률을 결정합니다. 구체적으로는 다음과 같습니다:

공식 주석: 위의 유도 과정을 통해 새 난이도에서의 채굴 성공 확률은 이전 난이도에서의 성공 확률에 매개변수 r을 곱한 값입니다.

마찬가지로, VDF의 난이도도 재계산되며, 이는 체크포인트 주기가 시간적으로 매초 발생할 수 있도록 유지하기 위한 목적입니다.

완전 복사의 인센티브 메커니즘

Arweave는 SPoRes 메커니즘을 통해 각 블록을 생성하는데, 이는 다음과 같은 가정에 기반합니다:

인센티브가 주어지면, 개별 채굴자든 집단 협력 채굴자든 완전한 데이터 복사본을 유지하는 것이 채굴의 최선의 전략으로 실행될 것입니다.

이전에 소개된 SPoRes 게임에서, 데이터 세트의 동일한 부분에 대한 두 개의 복사본이 방출하는 SPoA 해시 수는 전체 데이터 세트의 완전한 복사본과 동일합니다. 이는 채굴자에게 투기 행동의 가능성을 남깁니다. 따라서 Arweave는 이 메커니즘을 실제로 배포할 때 몇 가지 수정을 했으며, 프로토콜은 매초 잠금 해제되는 SPoA 도전 수를 두 부분으로 나누었습니다.

• 한 부분은 채굴자가 저장하는 파티션 중 하나를 지정하여 일정 수의 SPoA 도전을 방출합니다;
• 다른 부분은 Arweave의 모든 데이터 파티션 중 무작위로 하나의 파티션을 지정하여 SPoA 도전을 방출하며, 채굴자가 이 파티션의 복사본을 저장하지 않으면 이 부분의 도전 수를 잃게 됩니다.

여기서 아마도 여러분은 SPoA와 SPoRes 사이의 관계에 대해 혼란스러울 수 있습니다. 합의 메커니즘은 SPoRes인데, 왜 방출되는 것은 SPoA의 도전인가요? 사실 이들은 종속적인 관계입니다. SPoRes는 이 합의 메커니즘의 총칭으로, 채굴자가 수행해야 할 일련의 SPoA 증명 도전을 포함합니다.

이를 이해하기 위해, 우리는 이전 섹션에서 설명한 VDF가 SPoA 도전을 잠금 해제하는 데 어떻게 사용되는지를 살펴보겠습니다.

위 코드는 VDF(암호화 시계)를 통해 저장 파티션에서 일정 수의 SPoA로 구성된 회귀 범위를 잠금 해제하는 과정을 자세히 설명합니다.

1. 약 매초마다 VDF 해시 체인은 체크포인트(Check)를 출력합니다;
2. 이 체크포인트 Check는 채굴 주소(addr), 파티션 인덱스(index(p)), 그리고 원래 VDF 시드(seed)와 함께 RandomX 알고리즘을 사용하여 해시 값 H0를 계산합니다. 이 해시 값은 256비트 숫자입니다;
3. C1은 회귀 오프셋으로, H0를 파티션 크기 size(p)로 나눈 나머지로 생성되며, 이는 첫 번째 회귀 범위의 시작 오프셋이 됩니다;
4. 이 시작 오프셋에서 시작하는 연속 100 MB 범위 내의 400개의 256 KB 데이터 블록이 첫 번째 회귀 범위 SPoA 도전으로 잠금 해제됩니다.
5. C2는 두 번째 회귀 범위의 시작 오프셋으로, H0를 모든 파티션 크기의 합으로 나눈 나머지로 생성되며, 이는 두 번째 회귀 범위의 400개의 SPoA 도전을 잠금 해제합니다.
6. 이러한 도전의 제약은 두 번째 범위 내의 SPoA 도전이 첫 번째 범위의 해당 위치에도 SPoA 도전이 있어야 한다는 것입니다.

각 패키지된 파티션의 성능

각 패키지된 파티션의 성능은 각 파티션이 각 VDF 체크포인트에서 생성하는 SPoA 도전 수를 의미합니다. 채굴자가 파티션의 유일한 복사본 Unique Replicas를 저장할 경우, SPoA 도전 수는 채굴자가 동일한 데이터의 여러 백업 Copies를 저장할 때보다 많습니다.

여기서 "유일한 복사본" 개념은 "백업" 개념과 큰 차이가 있으며, 구체적으로는 과거의 글 《Arweave 2.6 아마도 사토시의 비전과 더 잘 맞을 것》의 내용을 읽어보시기 바랍니다.

채굴자가 파티션의 유일한 복사본 데이터만 저장했다면, 각 패키지된 파티션은 모든 첫 번째 회귀 범위의 도전을 생성하고, 저장 파티션 복사본의 수에 따라 해당 파티션 내의 두 번째 회귀 범위를 생성합니다. 만약 전체 Arweave 직조 네트워크에 m개의 파티션이 있고, 채굴자가 그 중 n개의 파티션의 유일한 복사본을 저장하고 있다면, 각 패키지된 파티션의 성능은 다음과 같습니다:

채굴자가 저장하는 파티션이 동일한 데이터의 백업일 경우, 각 패키지된 파티션은 여전히 모든 첫 번째 회귀 범위 도전을 생성합니다. 그러나 1/m의 경우에만 두 번째 회귀 범위가 이 파티션 내에 위치하게 됩니다. 이는 이러한 저장 전략 행동에 상당한 성능 처벌을 가져오며, SPoA 도전 수의 비율은 다음과 같습니다:

그림 1: 한 채굴자(또는 협력하는 채굴자 그룹)가 그들의 데이터 세트를 패키징 완료했을 때, 주어진 파티션의 성능이 향상됩니다.

그림 1의 파란색 선은 저장 파티션의 유일한 복사본 성능 perf_{unique}(n,m)이며, 이 그래프는 채굴자가 매우 적은 파티션 복사본만 저장할 때 각 파티션의 채굴 효율이 50%에 불과하다는 것을 직관적으로 보여줍니다. 모든 데이터 세트 부분을 저장하고 유지할 때, 즉 n=m일 때 채굴 효율은 최대 1에 도달합니다.

총 해시율

총 해시율(그림 2 참조)은 다음 방정식으로 주어지며, 각 파티션(per partition)의 값을 n으로 곱하여 얻습니다:

위 공식은 직조 네트워크(Weave) 크기가 증가함에 따라, 유일한 복사본 데이터를 저장하지 않을 경우, 처벌 함수(Penalty Function)가 저장 파티션 수의 증가에 따라 제곱으로 증가함을 나타냅니다.

그림 2: 유일한 데이터 세트와 백업 데이터 세트의 총 채굴 해시율

한계 파티션 효율성

이 프레임워크를 기반으로, 우리는 채굴자가 새로운 파티션을 추가할 때 직면하는 결정 문제를 탐구합니다. 즉, 그들이 이미 가진 파티션을 복사할 것인지, 아니면 다른 채굴자로부터 새로운 데이터를 얻어 유일한 복사본으로 패키징할 것인지입니다. 그들이 최대 가능 m개의 파티션 중 n개의 파티션의 유일한 복사본을 저장하고 있을 때, 그들의 채굴 해시율은 비례합니다:

따라서 새로운 파티션의 유일한 복사본을 추가하는 것의 추가 수익은:

이미 패키징된 파티션을 복사하는(더 작은) 수익은:

첫 번째 수를 두 번째 수로 나누면, 우리는 채굴자의 상대적 한계 파티션 효율성(relative marginal partition efficiency)을 얻습니다:

그림 3: 채굴자는 완전한 복사본을 구축하도록 유도되며(옵션 1), 이미 가진 데이터의 추가 복사본을 만드는 것(옵션 2)보다 더 유리합니다.

rmpe 값은 채굴자가 새로운 데이터를 추가할 때 기존 파티션을 복사하는 것에 대한 처벌로 볼 수 있습니다. 이 표현식에서 우리는 m을 무한대로 향하게 하여 처리한 다음, 서로 다른 n 값에서의 효율성 균형을 고려할 수 있습니다:

• 채굴자가 거의 완전한 데이터 세트 복사본을 가질 때, 복사본을 완료하는 보상이 가장 높습니다. 왜냐하면 n이 m에 가까워지고 m이 무한대로 향할 경우, rmpe 값은 3이 되기 때문입니다. 이는 거의 완전한 복사본일 때 새로운 데이터를 찾는 효율성이 기존 데이터를 재패키징하는 효율성의 3배라는 것을 의미합니다.
• 채굴자가 직조 네트워크(Weave)의 절반을 저장할 때, 예를 들어 n= 1/2 m일 경우, rmpe는 2입니다. 이는 새로운 데이터를 찾는 채굴자의 수익이 기존 데이터를 복사하는 수익의 2배라는 것을 나타냅니다.
• 낮은 n 값의 경우, rmpe 값은 1보다 크지만 항상 1에 가까워집니다. 이는 유일한 복사본을 저장하는 수익이 항상 기존 데이터를 복사하는 수익보다 크다는 것을 의미합니다.

네트워크가 성장함에 따라(m이 무한대로 향할 때), 채굴자가 완전한 복사본을 구축하려는 동기가 강화될 것입니다. 이는 협력 채굴 그룹의 형성을 촉진하며, 이러한 그룹은 최소한 하나의 데이터 세트의 완전한 복사본을 공동으로 저장합니다.

✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨✨

이 문서는 Arweave 합의 프로토콜 구축의 세부 사항을 주로 다루고 있으며, 이는 이 부분의 핵심 내용의 서두에 불과합니다. 메커니즘 소개와 코드에서 우리는 프로토콜의 구체적인 세부 사항을 매우 직관적으로 이해할 수 있습니다. 도움이 되기를 바랍니다.