书接上回，关于《다중 요인 모델을 사용하여 강력한 암호 자산 투자 포트폴리오 구축하기》 시리즈 기사 중, 우리는 네 편을 발표했습니다: 《이론 기초 편》、《데이터 전처리 편》、《요인 유효성 검증 편》、《대분류 요인 분석: 요인 합성 편》。

지난 편에서는 요인 공선성(요인 간 상관관계가 높은) 문제를 구체적으로 설명했습니다. 대분류 요인 합성을 진행하기 전에 요인 직교화를 통해 공선성을 제거해야 합니다.

요인 직교화를 통해 원래 요인의 방향을 재조정하여 서로 직교하게 만듭니다([fᵢ→,fⱼ→]=0, 즉 두 벡터가 서로 수직), 본질적으로 원래 요인을 좌표축에서 회전시키는 것입니다. 이러한 회전은 요인 간의 선형 관계를 변경하지 않으며 원래 포함된 정보를 변경하지 않고, 새로운 요인 간의 상관관계는 0이 됩니다(내적이 0이라는 것은 상관관계가 0이라는 것과 동치), 요인이 수익에 대한 설명력은 변하지 않습니다.

일, 요인 직교화의 수학적 유도

다중 요인 단면 회귀 관점에서 요인 직교화 체계를 구축합니다.

각 단면에서 전체 시장 토큰이 각 요인에서의 값을 얻을 수 있으며, N은 단면에서 전체 시장 토큰 수를 나타내고, K는 요인 수를 나타내며, fᵏ=[f₁ᵏ,f₂ᵏ,…,fᵏ]′는 전체 시장 토큰이 k번째 요인에서의 값을 나타내며, 각 요인에 대해 z-score 정규화 처리가 이루어졌습니다. 즉, fˉᵏ=0,∣∣fᵏ∣∣=1입니다.

Fₙ×ₖ=[f¹,f²,…,fᵏ]는 단면에서 K개의 선형 독립 요인 열 벡터로 구성된 행렬이며, 위의 요인이 선형 독립이라고 가정합니다(상관관계가 100% 또는 -100%가 아님, 직교화 처리의 이론적 기초).

Fₘₙ에 대해 선형 변환을 수행하여 새로운 요인 직교 행렬 F′ₘₙ=[f₁ᵏ,f₂ᵏ,…,fₙᵏ]′를 얻습니다. 새로운 행렬의 열 벡터는 서로 직교하며, 임의의 두 새로운 요인 벡터의 내적은 0입니다, ∀ᵢ,ⱼ,ᵢ≠ⱼ,[(f~ⁱ)'f~ʲ]=0.

Fₙ×ₖ에서 F~ₙ×ₖ로의 전이 행렬 Sₖ×ₖ을 정의합니다.

1.1 전이 행렬 Sₖ×ₖ

이제 전이 행렬 Sₖₖ을 구하기 시작합니다. 먼저 Fₙₖ의 공분산 행렬 ∑ₖₖ을 계산합니다. 그러면 Fₙₖ의 중첩 행렬 Mₖₖ=(N−1)∑ₖₖ입니다. 즉,

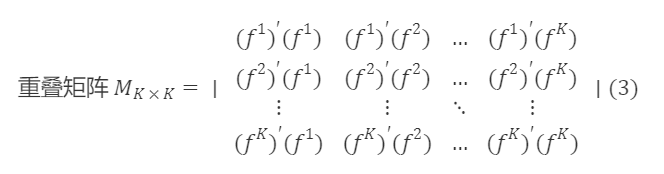
회전된 F~ₙ×ₖ는 직교 행렬입니다. 직교 행렬의 성질에 따라 AAᐪ=I이므로,

따라서,

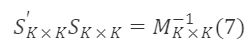
이 조건을 만족하는 Sₖₖ이 조건을 충족하는 전이 행렬입니다. 위의 공식의 일반 해는 다음과 같습니다:

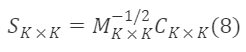
여기서 Cₖ×ₖ는 임의의 직교 행렬입니다.

1.2 대칭 행렬 Mₖ×ₖ⁻¹/²

이제 M∗ₖ×ₖ⁻¹/²를 구하기 시작합니다. M∗ₖ×ₖ는 대칭 행렬이므로, 다음과 같은 양의 정부호 행렬 Uₖ×ₖ가 존재합니다:

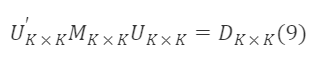
여기서,

U∗K×K,D∗K×K는 각각 M∗K×K의 고유 벡터 행렬과 고유 값 대각 행렬이며, U∗K×K′=Uₖ×ₖ⁻¹,∀ₖ,λₖ>0입니다. 공식 (13)에 의해

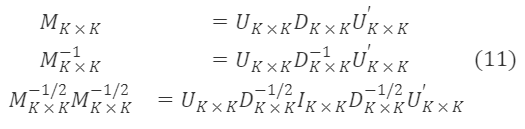
M∗ₖ×ₖ⁻¹/²는 대칭 행렬이며, U∗ₖ×ₖU∗ₖ×ₖ′=I∗ₖ×ₖ에 따라 위 식을 기반으로 M∗ₖ×ₖ⁻¹/²의 한 특해를 얻습니다:

여기서

M∗ₖ×ₖ⁻¹/²의 해를 공식 (6)에 대입하여 전이 행렬을 구할 수 있습니다:

여기서 Cₖ×ₖ는 임의의 직교 행렬입니다.

공식 (12)에 따르면, 어떤 종류의 요인 직교화도 서로 다른 직교 행렬 Cₖ×ₖ을 선택하여 원래 요인을 회전하는 것으로 변환할 수 있습니다.

1.3 공선성 제거에 주로 사용되는 3가지 직교 방법

1.3.1 슈미트 직교화

따라서 S∗K×K는 상삼각 행렬이며, C∗K×K=U∗K×KD∗K×ₖK⁻¹/²U∗K×K′S∗K×K입니다.

1.3.2 정규 직교화

따라서 Sₖ×ₖ=Uₖ×ₖDₖ×ₖ⁻¹/²이며, Cₖ×ₖ=Uₖ×ₖ입니다.

1.3.3 대칭 직교화

따라서 Sₖ×ₖ=Uₖ×ₖDₖ×ₖ⁻¹/²U′ₖ×ₖ이며, Cₖ×ₖ=Iₖ×ₖ입니다.

이, 세 가지 직교 방법의 구체적인 구현

1. 슈미트 직교화

선형 독립 요인 열 벡터 f¹,f²,…,fᵏ가 있을 때, 단계적으로 직교 벡터 집합 f~¹,f~²,…,f~ᵏ를 구성할 수 있으며, 직교화된 벡터는 다음과 같습니다:

그리고 f~¹,f~²,…,f~ᵏ를 단위화한 후:

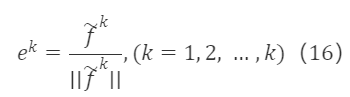
이러한 처리를 통해 표준 직교 기저 집합을 얻습니다. e¹,e²,…,eᵏ는 f¹,f²,…,fᵏ와 동치이며, 두 집합은 서로 선형적으로 표현할 수 있습니다. 즉, eᵏ는 f¹,f²,…,fᵏ의 선형 조합으로, eᵏ=βᵏ₁f¹+βᵏ₂f²+…+βᵏₖfᵏ입니다. 따라서 원 행렬 F∗K×K의 전이 행렬 S∗K×K는 상삼각 행렬의 형태입니다:

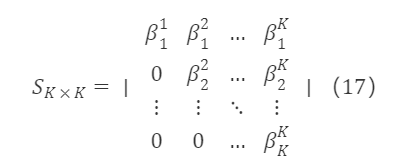
여기서

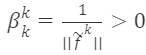
공식 (17)을 기반으로 슈미트 직교화에서 선택된 임의의 직교 행렬은 다음과 같습니다:

슈미트 직교화는 순차적 직교 방법이므로 요인 직교의 순서를 결정해야 합니다. 일반적인 직교 순서에는 고정 순서(다른 단면에서 동일한 직교 순서를 선택)와 동적 순서(각 단면에서 일정한 규칙에 따라 직교 순서를 결정)가 있습니다. 슈미트 직교화 방법의 장점은 동일한 순서로 직교화된 요인 간에 명시적인 대응 관계가 있지만, 직교 순서에 대한 통일된 선택 기준이 없으며, 직교화 후의 성능은 직교 순서 기준과 윈도우 기간 매개변수의 영향을 받을 수 있습니다.

# 슈미트 직교화
from sympy.matrices import Matrix, GramSchmidt
Schmidt = GramSchmidt(f.apply(lambda x: Matrix(x),axis=0),orthonormal=True)

f_Schmidt = pd.DataFrame(index=f.index,columns=f.columns)
for i in range(3):
    f_Schmidt.iloc[:,i]=np.array(Schmidt[i])
res = f_Schmidt.astype(float)

2. 정규 직교화

직교 행렬 Cₖ×ₖ=Uₖ×ₖ을 선택하면 전이 행렬은 다음과 같습니다:

여기서 U∗K×K는 고유 벡터 행렬로, 요인 회전에 사용되며, D∗K×K⁻¹/²는 대각 행렬로, 회전 후 요인의 스케일링에 사용됩니다. 여기서의 회전은 차원 축소를 하지 않는 PCA와 일치합니다.

# 정규 직교화
def Canonical(self):
  overlapping_matrix = (time_tag_data.shape[1] - 1) * np.cov(time_tag_data.astype(float))
  # 고유값과 고유벡터 가져오기
  eigenvalue, eigenvector = np.linalg.eig(overlapping_matrix)
  # np의 행렬로 변환
  eigenvector = np.mat(eigenvector)
  transition_matrix = np.dot(eigenvector, np.mat(np.diag(eigenvalue ** (-0.5))))
  orthogonalization = np.dot(time_tag_data.T.values, transition_matrix)
  orthogonalization_df = pd.DataFrame(orthogonalization.T,index = pd.MultiIndex.from_product([time_tag_data.index, [time_tag]]),columns=time_tag_data.columns)
  self.factor_orthogonalization_data = self.factor_orthogonalization_data.append(orthogonalization_df)

3. 대칭 직교화

슈미트 직교화는 과거 여러 단면에서 동일한 요인 직교 순서를 선택했기 때문에 직교화된 요인과 원래 요인 간에 명시적인 대응 관계가 있습니다. 반면, 정규 직교화는 각 단면에서 선택된 주성분 방향이 일관되지 않을 수 있어 직교 전후의 요인 간에 안정적인 대응 관계가 없을 수 있습니다. 따라서 직교화 후 조합의 효과는 직교 전후 요인 간의 안정적인 대응 관계에 크게 의존합니다.

대칭 직교화는 원래 요인 행렬에 대한 수정을 최소화하여 직교 기저 집합을 얻습니다. 이렇게 하면 직교화 후 요인과 원래 요인 간의 유사성을 최대한 유지할 수 있으며, 슈미트 직교화 방법에서처럼 직교 순서에 편향되지 않도록 합니다.

직교 행렬 Cₖ×ₖ=Iₖ×ₖ을 선택하면 전이 행렬은 다음과 같습니다:

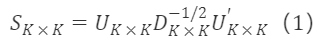
대칭 직교화의 성질:

1. 슈미트 직교화와 비교할 때, 대칭 직교화는 직교 순서를 제공할 필요가 없으며, 각 요인을 동등하게 대우합니다.
2. 모든 직교 전이 행렬 중에서 대칭 직교화 후의 행렬과 원래 행렬 간의 유사성이 가장 크며, 즉 직교 전후 행렬 간의 거리가 최소입니다.

# 대칭 직교화
def Symmetry(factors):
    col_name = factors.columns  
    D, U = np.linalg.eig(np.dot(factors.T, factors))  
    U = np.mat(U)
    d = np.diag(D**(-0.5))
    S = U*d*U.T 
    #F_hat = np.dot(factors, S) 
    F_hat = np.mat(factors)*S 
    factors_orthogonal = pd.DataFrame(F_hat, columns=col_name, index=factors.index)  
    return factors_orthogonal
res = Symmetry(f)

LUCIDA & FALCON에 대하여

Lucida （https://www.lucida.fund/ ）는 업계 선도적인 양적 헤지 펀드로, 2018년 4월 Crypto 시장에 진입했으며, 주로 CTA / 통계 차익 거래 / 옵션 변동성 차익 거래 등의 전략을 거래하고 있으며, 현재 관리 규모는 3000만 달러입니다.

Falcon （https://falcon.lucida.fund /）은 차세대 Web3 투자 인프라로, 다중 요인 모델을 기반으로 하여 사용자가 암호 자산을 "선택", "구매", "관리", "판매"할 수 있도록 돕습니다. Falcon은 2022년 6월 Lucida에 의해 인큐베이팅되었습니다.

더 많은 내용은 https://linktr.ee/lucida_and_falcon를 방문하십시오.