3.1 Secret Engine

各ゼロ知識証明システムは、アルゴリズムと多項式コミットメントスキームの2つの部分で構成されていることを認識しています。プログラムをゼロ知識証明（ZKP）に変換する初期段階はアルゴリズムに関わります。このプロセスは、これらの多項式間に特定の条件を確立することによって、それらの関係を明確にします。

私たちのゼロ知識証明システムは、標準のPlonKレシピに基づいて実装されており、高度にカスタマイズされたゲートを持ち、主に以下を含みます：

• ツール：基本的な算術回路、ハッシュ、ECC、zkshuffle、zkmatchmakingなど、ゲーム回路開発で使用されるさまざまなツールをサポートします。これらのツールに関する詳細情報は、私たちのGitHubリポジトリを訪問することをお勧めします。

• オンチェーンバリデーター：証明者と検証者のためにPLONK/ZKVMを最適化し、すべてのEVMチェーンの一般的な信頼性バリデーターをサポートします。

• アプリケーション特化型Plonk：アプリケーション特化型Plonkを基本的なZK証明として使用し、私たちのSDKが提供するさまざまなツールを使用して特定のゲーム回路を記述します。同時に、異なる仮想マシン（EVM/WASM/…）上の検証契約も提供し、異なるブロックチェーンシステムで動作し、オフチェーン証明とオンチェーン検証を実現します。

次に、Secret Engineから孵化した2つの重要なコンポーネント、zkshuffleとzkmatchmakingについて紹介します。

3.1.1 ZK shuffle SDK

3.1.1.1 イントロダクション

ポーカーゲームは非常に人気のあるカードゲームです。現実の生活では、ゲームの各参加者が互いに監視し合い、公平性を確保します。コンピューターネットワークの急速な発展に伴い、ネットワークで接続されたプレイヤーもポーカーゲームに参加する機会を得ましたが、ネットワーク環境でゲームの円滑な進行と公平性を確保することは大きな課題であり、これが心理ポーカー協定が解決しようとしている問題です。

心理ポーカーは、暗号学の原理に基づいて構築されたポーカーゲームであり、1979年にShamir、Rivest、Adlemanが最初の心理ポーカー協定を提案して以来【15】、心理ポーカーゲームの実現可能性が研究されてきました。心理ポーカーは通常のポーカーのプレイ方法に似ていますが、主な違いは、心理ポーカーが物理的なカードなしでネットワーク環境で行われ、すべてのプレイヤーが不誠実であると仮定され、つまり不正行為が存在することです。最初の心理ポーカー協定は二者間のポーカー協定であり、この協定には安全上の脆弱性があることが証明されています。文献【16】によれば、公平な心理ポーカーは以下の属性を満たす必要があります：

1. 一意性：従来のポーカーゲームでは、明示的なカードを通じて重複のないカードを検証します。心理ポーカー協定も同様の特性を保証する必要があります。

2. ランダム分布：従来のポーカーゲームでは、1人のプレイヤーがシャッフルを行い、他のプレイヤーがリアルタイムで観察できるため、シャッフルを行うプレイヤーは最終的なシャッフル結果を制御できません。

3. 機密性：いつでも、カード山が裏向きである場合、カード山内の任意のカードに関する情報を明らかにしてはなりません。また、プレイヤーがカードを引くとき、他のプレイヤーはそのカードに関する情報を取得できません。

4. 信頼できる第三者がいないこと：信頼できる第三者に依存することはできません。なぜなら、誰でも買収される可能性があり、絶対に信頼できる第三者はいないからです。

1987年、Crépeauは最初の安全な心理ポーカー協定を提案しました【17】。その後、心理ポーカー協定の提案が相次ぎましたが、多くの心理ポーカー協定の研究はTTPに基づいています。なぜなら、学界ではTTPを使用することが心理ポーカー協定の公平性を確保するための有効な手段であると広く考えられているからです。しかし、ポーカーは娯楽やレクリエーションのゲームであり、多くのシナリオでは第三者が存在せず、特にブロックチェーン技術が関与する場合、信頼できる第三者を確保することは非常に困難です。したがって、PPTなしで公平な心理ポーカー協定を実現する方法は重要な意義を持ちます。Barnett-Smart協定【18】は2003年に提案され、ElGamalおよびPailler暗号システムに基づく2つの解決策を提供しましたが、Pailler暗号スキームには安全上の制限があり、共謀者の数が(N-1)/2を超えないと仮定されています。その後、Castellà-Roca協定【19】が提案され、異なる暗号スキームを採用し、シャッフルプロセスもBarnett-Smart協定よりも速くなりました。

心理ポーカー協定のコストは主にシャッフル部分に集中していますが、今日のゼロ知識証明アルゴリズムは急速に発展しており、geometry【20】【21】は、シャッフルプロセスがもはやボトルネックではなく、Barnett-Smart協定が完全なカードゲーム協定を複数の安全なサブプロトコルに分割する必要があると考えています：カードの生成、マスキング、再マスキング、シャッフルなど、これらのステップは簡単にプラグアンドプレイで実現でき、その安全性の仮定もDecisional Diffie-Hellmanに基づいています。したがって、私たちのメンタルポーカー協定は主にBarnett-Smart協定を参考にしていますが、同時に一組のトランプに対するzkShuffleが大量の楕円曲線計算を伴うことを考慮し、その回路規模が非常に大きくなることを認識しています。この問題を解決するために、私たちはzkshuffleに優しいTurboPlonk【22】アルゴリズムを再設計し、回路ゲートの規模を大幅に削減しました。

3.1.1.2 基本概念

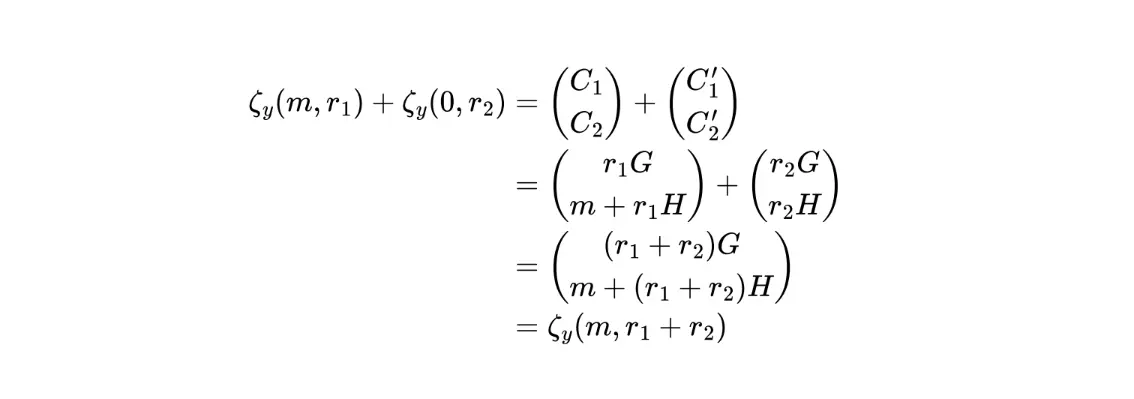
注：n-out-of-n threshold EIGamal encryption【23】

3.1.1.3 心理ポーカー協定

メンタルポーカー協定は1つの協定ではなく、一連のサブプロトコルを含み、各サブプロトコルは1つの行動を担当します。

• 鍵生成：

• 各プレイヤーの公開鍵と秘密鍵のペアを生成
• すべてのプレイヤーの公開鍵を集約して1つの公開鍵を生成

• マスキング：

• マスキング関数は、集約された公開鍵の下でのElGamal暗号関数です

• シャッフルと再マスキング：

• カードをシャッフルしてランダム化を達成
• シャッフル後のカードを再度マスク

• アンマスク：

• カードをデコードして実際のカード情報を取得

鍵生成プロトコル

マスキングプロトコル

再マスキングプロトコル

シャッフル引数

アンマスクプロトコル

3.1.1.4 シャッフルフレンドリーPLONKアルゴリズム

シャッフルプロトコルは主に2つの部分から構成されます：1) カードの置換；2) カードの再マスキング；このうち再マスキング操作は楕円曲線計算を含み、具体的には1つの定数ベーススカラー乗算、1つの非定数ベーススカラー乗算、2つの曲線加算が含まれます。非最適化TurboPlonkカスタムゲートを使用して算術回路を記述すると、1枚のカードの再マスキングの回路ゲート数は596+1622+2=2220になります。したがって、完全なカードセット（52枚）の場合、回路ゲート数は115440に達し、置換関連の回路は含まれていません。したがって、非最適化のTurboPlonkを使用して算術回路を記述すると、シャッフル時間は非常に長くなります。この問題を解決するために、私たちはTurboPlonkを改造してシャッフル運算に優しくし、検証の結果、再マスキング操作にはわずか85ゲートが必要です。

注：bowe hopwood【24】

3.1.1.5 オンチェーン検証

さらに、私たちの実践では、オンチェーン検証のガス費が高い問題にも直面しました。ここでは、主に私たちの最適化の知見を共有します。

Verify reveal 1枚のカードを解読するには、他のプレイヤーが対応する開示情報を提供し、開示の正確性を検証するための証明を提供する必要があります。既存のGeometryの現実【25】は、chaum pedersenプロトコルに基づいて開示証明を構築しました。chaum pedersenは点乗算を必要とし、点乗算操作は非常に高価です。主に現在のイーサリアムがBaby Jubjubという曲線のプリコンパイル契約をサポートしていないためです。テスト結果に基づくと、Geometryに基づいて実装された場合、開示証明のガス費は7629888に達し、これは明らかに受け入れられません。

Baby JubjubがBN254の内蔵曲線であることを考慮すると、Snarkを使用して開示証明を行うことができ、ガスの分析【26】によれば、Groth16を使用した開示証明のオンチェーン検証コストは約200kに過ぎず、これはほぼ原生の検証方法の30倍の削減です。原生の検証方法と比較して、これは非常に良い選択のようです。開示回路は以下の通りです：

将来的には、proofの集約を行い、ガスをさらに節約します。

Verify shuffle テキサスホールデムゲームでは、シャッフルされた結果をオンチェーンに保存する必要があります。これは現在のシャッフル結果としてだけでなく、後続のシャッフル回路の公開入力としても使用されます。しかし、1組のトランプには52枚あり、合計208個のuint256型データがあり、そのオンチェーンストレージコストは高価です。

私たちの提案は、オンチェーンに保存するトランプデータの一部だけを保存することです。具体的には、2n+5枚のカードを保存する必要があります。ここでnはプレイヤーの数です。私たちのゲームは最大で6人のプレイヤーを同時にサポートするため、最大で17枚のカードしか使用されません。これは、最終的にオンチェーンに保存する必要があるのは17枚のカードだけであり、ストレージコストを2/3削減できることを意味します。

最終的にオンチェーンに保存する必要があるのは17枚のカードだけですが、前述のようにオンチェーンストレージの別の目的は、これらのカードが後続のシャッフル回路の公開入力としても使用されることです。したがって、17枚のカードだけを保存すると、シャッフルの正確性を検証できなくなります。この問題を解決するために、シャッフル回路は完全なトランプのハッシュ値を追加で出力し、オンチェーンに保存します。zkShuffleを検証する際には、回路の公開入力として使用され、シャッフルの正確性が保証されます。

3.1.2 ZK matchmaking SDK

マッチメイキングは、プレイヤーのレベルに基づいてゲームをマッチングするメカニズムであり、プレイヤーがゲーム内で実力のある対戦相手と対戦できるようにし、公平で楽しいゲーム体験を提供することを目的としています。マッチメイキングの核心的な目標は以下の2つに要約できます：

• 公平な対戦：実力が同等のプレイヤー同士の対戦を提供し、双方の勝利の確率ができるだけ50%に傾くようにします。

• 予測不可能性：マッチングプロセスは予測不可能であり、最終的な対戦者は予測できません。

全体のプロセス

1. Proverとして申請する際、契約に対して種を約束する必要があります。この種はProverのみが知っています。

2. プレイヤーがゲーム参加リクエストを送信します。

3. ソーターはリクエストを受け取った後、階層戦略に基づいてソートし、生成されたキューを契約と証明者にそれぞれ送信します。

4. ProverはzkSnarkに基づいて異なるキューをランダムにマッチングし、マッチングの結果はProverが約束した種、入力されたキュー、およびオンチェーンのランダム数（確定的だが予測不可能）に依存し、マッチングの結果と証明を契約に送信します。

5. 契約はオンチェーン検証を行い、検証が通れば、プレイヤーはマッチング結果に基づいてゲームに参加します。

ブロックチェーン上では、block hashのようなオンチェーンのランダム数を簡単に取得できますが、これはマイナーや検証者によるブロック保持攻撃の影響を受け、block hashのようなオンチェーンのランダム数は十分に安全ではなく、マッチメイキングの予測不可能性も脅かされます。検証可能なランダム関数（VRF）は、検証特性を持つランダム数生成器であり、統計的に均一で予測不可能なランダム出力を生成でき、その出力は検証可能であり、私たちのオンチェーンランダム数に対する良い解決策を提供します。VRFの原理を簡単に理解してみましょう。入力としてseedを受け取り、ランダム数を出力します。

オンチェーンのランダム数に加えて、予測不可能性はProverが約束した種にも依存します。私たちはProverがランダム数を無造作に漏らさないように罰則メカニズムを構築します。

参考文献：

【15】A. Shamir, R. L. Rivest and L. M. Adleman, Mental poker, Technical report LCS/TM-125, Massachusetts Institute of Technology, April 1979.
【16】Crépeau C. A secure poker protocol that minimizes the effect of player coalitions, in: Conference on the Theory and Application of Cryptographic Techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 1985: 73--86.
【17】C. Crepeau, A zero-knowledge poker protocol that achieves confidentiality of the players' strategy or how to achieve an electronic poker face, in: Advances in Cryptology -- Crypto 086, Lecture Notes in Computer Science 263, Springer-Verlag, Berlin (1987), 239--247.
【18】A. Barnett and N. Smart, Mental poker revisited, in: Cryptography and Coding, Lecture Notes in Computational Science 2898, Springer-Verlag, Berlin (2003), 370--383.
【19】J. Castellà-Roca, Contributions to mental poker, Ph.D. Thesis, Autonomous University of Barcelona, Doctoral Programme in Computer Science and Artificial Intelligence, 2005.
【20】N Mohnblatt, A Novakovic and K Gurkan, Mental Poker in the Age of SNARKs - Part 1,
https://geometry.xyz/notebook/mental-poker-in-the-age-of-snarks-part-1
【21】N Mohnblatt, A Novakovic and K Gurkan, Mental Poker in the Age of SNARKs - Part 1,
https://geometry.xyz/notebook/mental-poker-in-the-age-of-snarks-part-2
【22】Gabizon A, Williamson Z J. The turbo-plonk program syntax for specifying snark programs, in: ZKProof Workshop. 2020, 3.
【23】Desmedt Y. Threshold cryptosystems, in: International Workshop on the Theory and Application of Cryptographic Techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 1992: 1--14.
【24】https://github.com/arkworks-rs/crypto-primitives/tree/main/crypto-primitives/src/crh/bowe_hopwood.

【25】https://github.com/geometryxyz/mental-poker/blob/main/barnett-smart-card-protocol/src/discretelogcards/mod.rs#L320.

【26】Todd Norton, Groth16 Verification Gas cost,https://hackmd.io/@nebra-one/ByoMB8Zf