書接上回、について《多因子モデルを用いた強力な暗号資産投資ポートフォリオの構築》シリーズの記事の中で、私たちはすでに4篇を発表しました：：《理論基礎篇》、《データ前処理篇》、《因子有効性検証篇》、《大類因子分析：因子合成篇》。

前回の記事では、因子共線性（因子間の相関が高い）について具体的に説明しました。大類因子合成を行う前に、因子の直交化を行い、共線性を排除する必要があります。

因子の直交化を通じて、元の因子の方向を再調整し、相互に直交させます（[fᵢ→,fⱼ→]=0、つまり2つのベクトルが互いに垂直であること）、本質的には元の因子の座標軸上の回転です。この回転は因子間の線形関係を変えず、元々含まれている情報も変えず、新しい因子間の相関はゼロになります（内積がゼロであることは相関がゼロであることと同等です）、因子が収益に対する説明度は変わりません。

一、因子直交化の数学的導出

多因子の横断回帰の観点から、因子直交化の体系を構築します。

各横断面で全市場のトークンが各因子上での値を取得できます。Nは横断面上の全市場トークンの数を表し、Kは因子の数を表します。fᵏ=[f₁ᵏ,f₂ᵏ,…,fᵏ]′は全市場トークンが第kの因子上での値を表し、各因子はzスコアの正規化処理が施されています。すなわち、fˉᵏ=0,∣∣fᵏ∣∣=1です。

Fₙ×ₖ=[f¹,f²,…,fᵏ]は横断面上のK個の線形独立な因子列ベクトルからなる行列であり、上記の因子が線形独立である（相関が100%または-100%でない、直交化処理の理論的基礎）と仮定します。

Fₘₙに対して線形変換を行うことで、新しい因子直交行列F′ₘₙ=[f₁ᵏ,f₂ᵏ,…,fₙᵏ]′を得ます。新しい行列の列ベクトルは互いに直交しており、任意の2つの新しい因子ベクトルの内積はゼロです。∀ᵢ,ⱼ,ᵢ≠ⱼ,[(f~ⁱ)'f~ʲ]=0。

Fₙ×ₖからF~ₙ×ₖへの遷移行列Sₖ×ₖを定義します。

1.1 遷移行列Sₖ×ₖ

以下に遷移行列Sₖₖを求めます。まず、Fₙₖの共分散行列∑ₖₖを計算します。すると、Fₙₖの重複行列Mₖₖ=(N−1)∑ₖₖとなります。

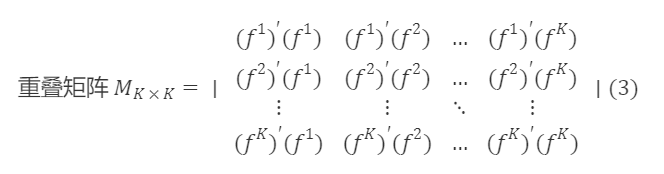
回転後のF~ₙ×ₖは直交行列であり、直交行列の性質によりAAᐪ=Iとなるため、次のようになります。

したがって、

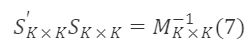
この条件を満たすSₖₖが条件を満たす遷移行列となります。上記の公式の一般解は次の通りです：

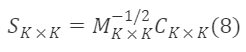
ここで、Cₖ×ₖは任意の直交行列です。

1.2 対称行列Mₖ×ₖ⁻¹/²

次にM∗ₖ×ₖ⁻¹/²を求めます。M∗ₖ×ₖは対称行列であるため、正定値行列Uₖ×ₖが存在し、次の条件を満たします：

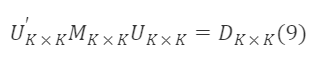
ここで、

U∗K×K,D∗K×KはそれぞれM∗K×Kの固有ベクトル行列と固有根対角行列であり、U∗K×K′=Uₖ×ₖ⁻¹,∀ₖ,λₖ>0です。公式（13）から次のように得られます：

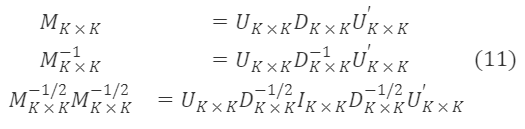
M∗ₖ×ₖ⁻¹/²は対称行列であり、U∗ₖ×ₖU∗ₖ×ₖ′=I∗ₖ×ₖであるため、上式に基づいてM∗ₖ×ₖ⁻¹/²の特解は次のようになります：

ここで

M∗ₖ×ₖ⁻¹/²の解を公式（6）に代入することで遷移行列を求めることができます：

ここで、Cₖ×ₖは任意の直交行列です。

公式（12）に基づき、任意の因子の直交は異なる直交行列Cₖ×ₖを選択することで元の因子を回転させることができます。

1.3 共線性を排除するために主に使用される3つの直交方法

1.3.1 シュミット直交

したがって、S∗K×Kは上三角行列であり、C∗K×K=U∗K×KD∗K×ₖK⁻¹/²U∗K×K′S∗K×Kとなります。

1.3.2 規範直交

したがって、Sₖ×ₖ=Uₖ×ₖDₖ×ₖ⁻¹/²、Cₖ×ₖ=Uₖ×ₖとなります。

1.3.3 対称直交

したがって、Sₖ×ₖ=Uₖ×ₖDₖ×ₖ⁻¹/²U′ₖ×ₖ、Cₖ×ₖ=Iₖ×ₖとなります。

二、3つの直交方法の具体的な実装

1.シュミット直交

線形独立な因子列ベクトルf¹,f²,…,fᵏがあるとします。これを用いて正交ベクトル群f~¹,f~²,…,f~ᵏを逐次構築できます。正交化されたベクトルは次のようになります：

そして、f~¹,f~²,…,f~ᵏを単位化すると：

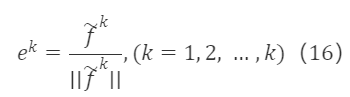
以上の処理を経て、標準正交基を得ます。e¹,e²,…,eᵏはf¹,f²,…,fᵏと等価であり、両者は相互に線形表示できます。すなわち、eᵏはf¹,f²,…,fᵏの線形結合であり、eᵏ=βᵏ₁f¹+βᵏ₂f²+…+βᵏₖfᵏとなります。したがって、元の行列F∗K×Kの遷移行列S∗K×Kは上三角行列となり、形は次のようになります：

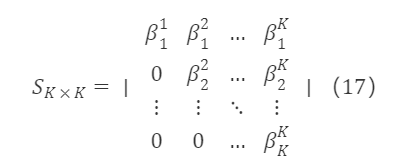
ここで

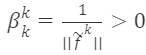
公式（17）に基づき、シュミット直交で選択された任意の直交行列は次のようになります：

シュミット直交は順序直交法であるため、因子直交の順序を決定する必要があります。一般的な直交順序には固定順序（異なる横断面で同じ直交順序を取る）と動的順序（各横断面で一定のルールに基づいてその直交順序を決定する）があります。シュミット直交法の利点は、同じ順序で直交する因子に明示的な対応関係があることですが、直交順序には統一された選択基準がなく、直交後のパフォーマンスは直交順序基準とウィンドウ期間パラメータの影響を受ける可能性があります。

# シュミット直交化
from sympy.matrices import Matrix, GramSchmidt
Schmidt = GramSchmidt(f.apply(lambda x: Matrix(x),axis=0),orthonormal=True)

f_Schmidt = pd.DataFrame(index=f.index,columns=f.columns)
for i in range(3):
    f_Schmidt.iloc[:,i]=np.array(Schmidt[i])
res = f_Schmidt.astype(float)

2.規範直交

直交行列Cₖ×ₖ=Uₖ×ₖを選択すると、遷移行列は次のようになります：

ここでU*K×Kは固有ベクトル行列であり、因子の回転に使用され、D∗K×K⁻¹/²は対角行列であり、回転後の因子のスケーリングに使用されます。この回転は次元削減を行わないPCAと一致します。

# 規範直交
def Canonical(self):
  overlapping_matrix = (time_tag_data.shape[1] - 1) * np.cov(time_tag_data.astype(float))
  # 固有値と固有ベクトルを取得
  eigenvalue, eigenvector = np.linalg.eig(overlapping_matrix)
  # npの行列に変換
  eigenvector = np.mat(eigenvector)
  transition_matrix = np.dot(eigenvector, np.mat(np.diag(eigenvalue ** (-0.5))))
  orthogonalization = np.dot(time_tag_data.T.values, transition_matrix)
  orthogonalization_df = pd.DataFrame(orthogonalization.T,index = pd.MultiIndex.from_product([time_tag_data.index, [time_tag]]),columns=time_tag_data.columns)
  self.factor_orthogonalization_data = self.factor_orthogonalization_data.append(orthogonalization_df)

3.対称直交

シュミット直交は過去のいくつかの横断面で同じ因子直交順序を取るため、直交後の因子と元の因子には明示的な対応関係があります。一方、規範直交では各横断面で選択される主成分の方向が一致しない可能性があり、直交前後の因子には安定した対応関係がないことがあります。このように、直交後の組み合わせの効果は、直交前後の因子に安定した対応関係があるかどうかに大きく依存します。

対称直交は元の因子行列の変更を最小限に抑えつつ、一組の直交基を得ることを目指します。これにより、直交後の因子と元の因子の類似性を最大限に保持できます。また、シュミット直交法のように直交順序の前方に偏る因子を避けることができます。

直交行列Cₖ×ₖ=Iₖ×ₖを選択すると、遷移行列は次のようになります：

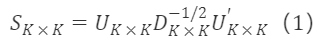
対称直交の性質：

1. シュミット直交と比較して、対称直交は直交順序を提供する必要がなく、各因子を平等に扱います。
2. すべての直交遷移行列の中で、対称直交後の行列と元の行列の類似性が最大であり、直交前後の行列の距離が最小です。

# 対称直交
def Symmetry(factors):
    col_name = factors.columns  
    D, U = np.linalg.eig(np.dot(factors.T, factors))  
    U = np.mat(U)
    d = np.diag(D**(-0.5))
    S = U*d*U.T 
    #F_hat = np.dot(factors, S) 
    F_hat = np.mat(factors)*S 
    factors_orthogonal = pd.DataFrame(F_hat, columns=col_name, index=factors.index)  
    return factors_orthogonal
res = Symmetry(f)

LUCIDA & FALCONについて

Lucida （https://www.lucida.fund/ ）は業界をリードする量的ヘッジファンドで、2018年4月にCrypto市場に参入し、主にCTA / 統計的アービトラージ / オプションボラティリティアービトラージなどの戦略を取引しており、現在の管理規模は3000万ドルです。

Falcon （https://falcon.lucida.fund /）は新世代のWeb3投資インフラであり、多因子モデルに基づいて、ユーザーが暗号資産を「選ぶ」、「買う」、「管理する」、「売る」手助けをします。Falconは2022年6月にLucidaによって孵化されました。

詳細については、https://linktr.ee/lucida_and_falconをご覧ください。