Uniswap v3 数学洞察：オプションがポジションとどのように組み合わさるか

撰文：ck.eth

編輯：Lylia， Antalpha Labs

原シリーズは全6部であり、これは第5部です。この部分では、オプションがポジションとどのように組み合わさるかを引き続き紹介します。このシリーズの前のポジション戦略についての一定の理解が必要です。より多くの人々がUniswap V3に関する有用な情報にアクセスし、理解できるように、シリーズ記事を翻訳しました。これにより、中国語の読者はUniswap v3のメカニズムと投資戦略の選択についてより深く理解できるようになります。この翻訳を読む際には、いつでも原文を参照して、詳細情報を得ることができます。

Uniswapの収益の凸性リスクの非線形性 / Theta-Gammaのボラティリティ。https://www.math3d.org/WvsEXvTWD

簡潔に言えば：

• Uniswap v2とv3のギリシャ解決策を示しています
• インタラクティブなdesmosファイルで、Uniswapv3を使用してアジアオプション、ヨーロッパオプション、バシリエオプションをヘッジする解決策を提供しています。
• desmosを使用してLPヘッジの蓄積戦略を示しています。
• LVRを引き起こす歴史と代替的な導出を説明しています。

ギリシャパラメータ - Uniswap v2

100%をLPポジションに割り当てるのではなく、一部をX資産に割り当て、残りをX資産をショートして発散損失を減少させる方が良いです。しかし、発散損失を完全に排除することはできません。その結果、支払い構造は崖から丘に変わります。ギリシャパラメータは、LPポジションの価値が他の変数（例えば、時間、ボラティリティ、金利）に対してどれだけ敏感であるかを示します。私たちは第4部でデルタとガンマを紹介しました。LPのギリシャパラメータは有用で、オプションのギリシャパラメータと組み合わせて価格の乖離を相殺することができます。例えば、価格が変動したり、ボラティリティが変化したり、時間が経過したりする場合の効果、すなわちデルタとガンマです。ギリシャパラメータの数値は、さまざまな要因がLPポジションの価格に与える影響を示しています。

v2のインタラクティブなdesmosファイル：https://www.desmos.com/calculator/inwy6djhhm

注意すべきは、オプションと比較して、UniswapのギリシャパラメータはLPポジションの価格が下落する際に無限に近づく傾向があることです。上の図ではx=0で破線で示されています。これらのテールリスクを削減するために、v3の集中範囲を使用することができます。

ギリシャパラメータ - 集中LP範囲v3

univ3ギリシャパラメータのdesmosファイル：https://www.desmos.com/calculator/l8sqzlwkf5

範囲pa（下限）~pb（上限）を集中させるほど、私たちのデルタΔとガンマΓはより敏感になります。ガンマが負であることに注意してください。これは、私たちのLP支払いが凹形の黒い形状を持つことを意味します。私たちのシータ/Θ/期待コストも増加し、金利感度ρは基本的に影響を受けません。

しかし、単一のLPポジションの支払い図はオプションと一致するかもしれませんが、他のギリシャパラメータは一致しないかもしれません。

LPギリシャパラメータは通常のオプションとは異なります：https://www.desmos.com/calculator/nyuw7sybin

ここでは、単一のLP範囲のコールオプションがありますが、他のギリシャパラメータは固定されていません。

使用できるテクニックは、LPポジションをヘッジする方法を見つけるのではなく、まず市場で行使価格（K）と暗黙のボラティリティ（σ_iv）および満期（t）を持つオプションを見つける必要があります。その後、対数正規分布に従う一連のLPポジションを構築できます。これは最初にダン・ロビンソン（Dan Robinson）のUniswap v3に関する正規分布流動性フィンガープリンツに触発された ^[1]^ものです。価格空間でのLPポジションの対数正規分布の粒度化は、ギリシャパラメータを平滑化することを可能にします：

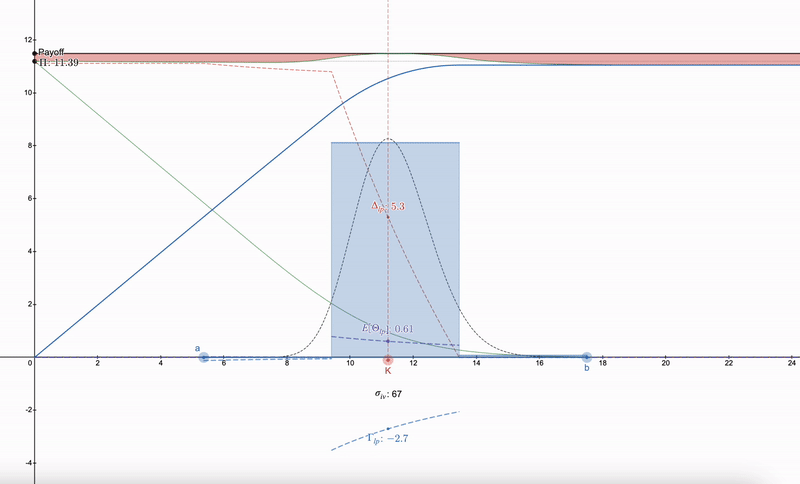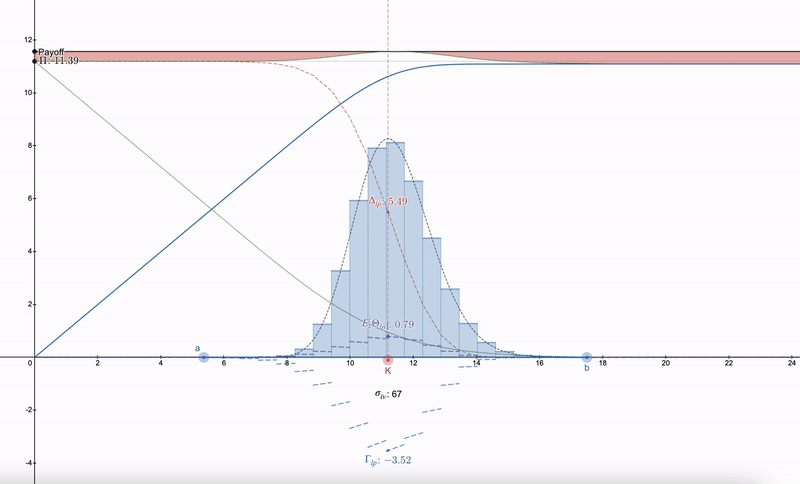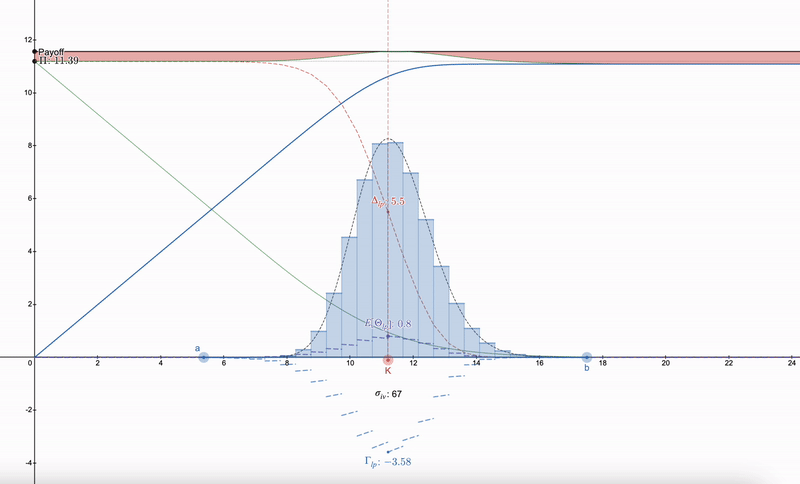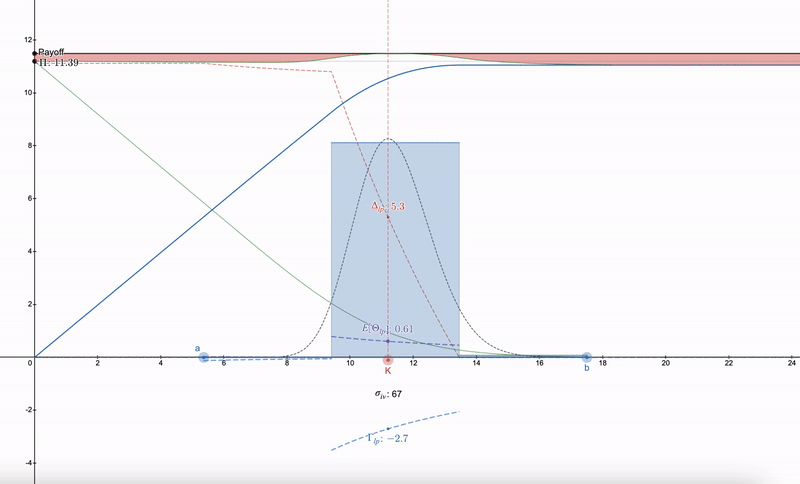
LPギリシャはオプションに似て始まることに注意してください。価格が下がるにつれて、LPポジションの多様性により、次の範囲に切り替えることができます。7つ以上のLPポジションは収益の減少をもたらします。

奇妙なことに、対数正規分布で100％の支払いをキャンセルすることは非常に困難なようです（もし私が間違っていたら訂正してください）。しかし、対数正規流動性フィンガープリンツがDiracデルタ関数に近づくと、上記の差異（上の図で赤色で視覚化されている）は消えます。例えば、アジアオプションはちょうど対数正規分布に従いますが、意外なことに、価格に対してより敏感で、ΔとΓがより鋭くなります。アジアオプションのボラティリティは通常のオプションの1/√3であるため、支払いの乖離に対する影響は小さくなります：

ヨーロッパのプットオプションを使用してLPポジションの組み合わせをヘッジし、その等価のアジアプットオプションでヘッジします。

1つのLPポジションはおおよそヨーロッパオプションに一致しますが、平滑なギリシャパラメータを無視し、一連のLPポジションはギリシャ文字を平滑化しますが、丘を残します。このトレードオフは、将来的に潜在的な調整/傾斜流動性フィンガープリンツによって改善される可能性があります。

LPヘッジ戦略

一方で、凹形LP支払いをキャンセルすることに興味がない場合、desmosファイル: https://www.desmos.com/calculator/khvbqzncg9を使用することができます。さまざまな支払い方法がどのように機能するかを確認するためにも使用できます。以下は、発生する可能性のある一連の支払いの例です。

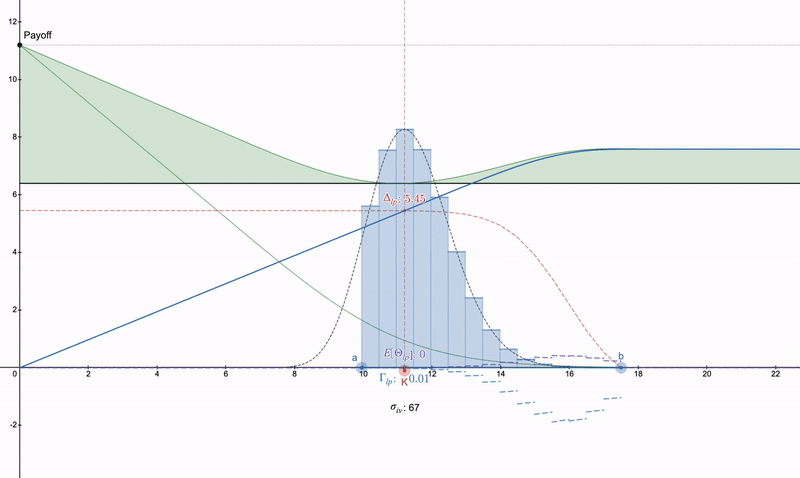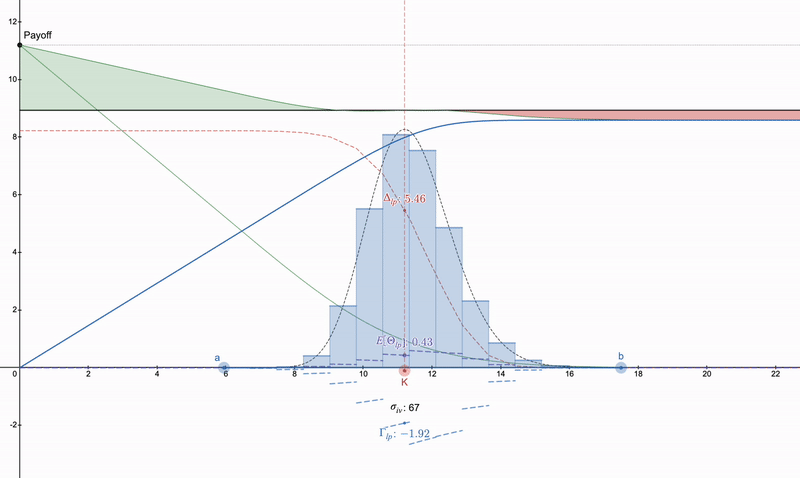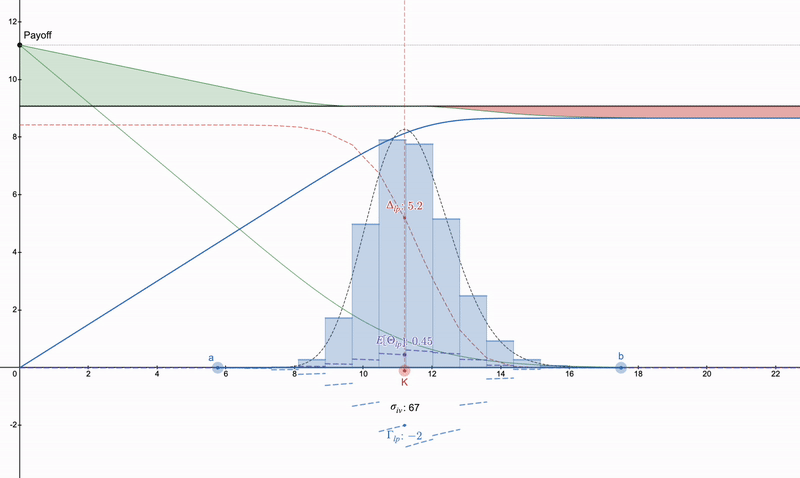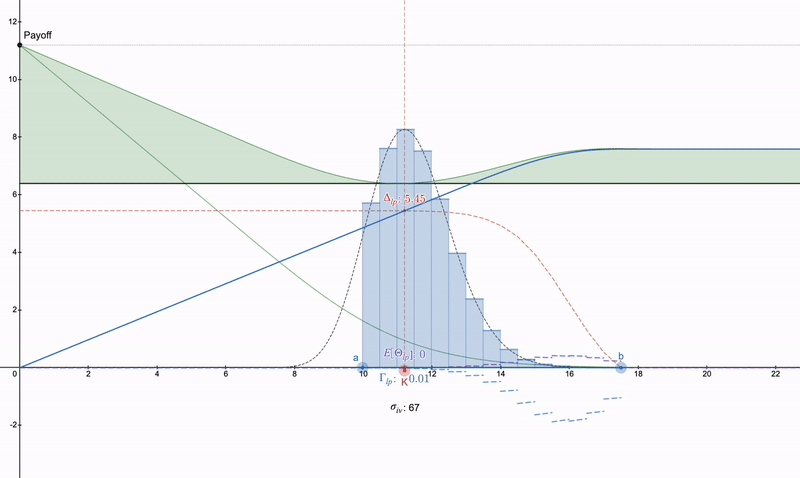
垂直プットスプレッド>>プットオプション>>ある種のロングストラドル。注意すべきは、シータの減衰により、プットオプションは時間の経過とともに悪化し、LPポジションは手数料のために増加する可能性があることです。

v3の興味深い特性の1つは、paの流動性を現在の価格のちょうど75％またはそれ以下に集中させ、pbを現在の価格に設定すると、X資産の価値が25％でピークに達することです。これは、資産を蓄積しようとする人々にとって一定の戦略的価値を持つかもしれません。

ダン・ロビンソンのv3ツール：https://twitter.com/danrobinson/status/1430678225945042945

このような単一の範囲を市場のプットオプションと組み合わせて、以下の支払いを得ることができます：https://www.desmos.com/calculator/a8y3pl3t03：

市場からプットオプションパラメータを抽出できます。時間が経つにつれて、価格が十分に早く下がらなければ、オプションの価値は下がります。

このような戦略は、本質的に価格の下落を求めて将来の資産を蓄積し、手数料を稼ぐことを目的としています。オプションがない場合、これはよりリスクの高い方法に変わり、実行者が資産の反発に対して非常に強い信念を持っている場合にのみ意味があります。ただし、これはいかなる財務アドバイスにも該当しないことに注意してください。私は単に数学的な計算を行っているだけです。

歴史的な深掘りがLVRを引き起こす：

第4部で、私はLPポジションの凹形と収益の関係を指摘し、歴史とLPの発散損失/損失と再平衡（LVR）の観点からそれを拡張したいと考えています。

タレブは、リスクとリターンの非線形関係を最初に書いたのはルイ・バシリエ ^[2]^であり、1900年のTheory de la Speculation ^[3]^において、フーリエの熱方程式との類似性に起因すると指摘しています。偶然にも、ランベールはファインマン-カックの方法を使用して集中LPポジションの価値を解決しました ^[4]^。

「Theory de la Speculation」の46ページ。定数が二乗され、dtとdx²があります！

バシリエの方程式は、漂流率がゼロに設定されたブラック-ショールズ-マートン方程式のわずかに再配置された形です ^[5]^。

資産価格の時間変化は、ボラティリティと曲率に関連しています。

LHSはシータ-Θ、RHSは曲率ガンマΓであり、負号のために凹形になります。次に、ゼロアンジェリス、エヴァンズ、チトラ ^[6]^は、AMMのLPポジションは凹形の支払い関数を持たなければならないと指摘しています。CurveのCSMM ^[7]^からForgy＆Lau ^[8]^の全対称流動性曲線空間に至るまで、すべてのLPは凹形であるべきです。

右側の方程式の凹性に基づくと、市場メーカー（LP）ポジション自体はプレミアムを持たなければなりません。プレミアムがなければ、以下の平等が破られ、単純にそのようなLPポジションを借りて一部の基礎資産を購入し、ボラティリティの増加を利用するために永続的なロングストラドルを構築することができます。

バシリエ等価/BSM動的ヘッジ - 凹形命令の収益と凸性命令のコストと呼ばれます。数学的表現：

収益 ∝ リスク × 凹性（負の凸性）。付録にBKの導出があります。

Uniswapのシータギリシャ値を求める際 ^[9]^、LPポジションの二次導関数を上記の式に代入することで、LVRと同じ方程式を得ることができます ^[10]^。

式16。バシリエ等価のガンマが-L/2sqrt(x)³であれば、同じ結果が得られます。

LVR論文図2は、上記の不変のxy=k図からvol²/8 LVR関係を導出し、凹形LP収益をもたらしました。

これは偶然ではなく、異なる角度からの人々が同じ結論に達しています。ランベールは実際に漂流率を含んでいます ^[11]^が、他の人々はそれを除外しています ^[12]^。

これらのモデルはすべて、最初に伊藤引理のブラウン運動（BM） ^[13]^に由来するガウス分布を仮定しており、内部の-σ²/2項が得られます。この項はアンジェリス、エヴァンズ、チトラの最終方程式にも現れます ^[6]^が、デジタル資産、特にステーブルコインはHurst指数>0.5を示し、フラクタルBMの挙動を示唆しています ^[14]^。セップとラフモノフも、ランダムボラティリティの手法がデジタル資産の傾斜暗黙のボラティリティ構造に適用されることを指摘しています ^[15]^。

最も持続的なデジタル資産の対数-対数ヒストグラムの尾部収益を調査することで、非ガウスの尾部も観察されました。

BTC-USDヒストグラム収益の核密度平滑化が青で表示されています

ヒストグラムの形状を考慮すると、Uniswap v2の全範囲均一分布を深く掘り下げ、ガウスの崖を超えて、市場メーカーに適したレバレッジ（LVR）シータ値を深く理解する必要があります。

50+分布の対数-対数ヒストグラム。指数法則と幂法則が深淵で私たちを待っています。

付録：

バシリエ等価の導出。

バシリエ等価から得られたUniswap LPポジションのLVR。

参考文献：

https://www.desmos.com/calculator/l1oivvaptt

https://www.maths.usyd.edu.au/u/UG/SM/MATH3075/r/HaugTaleb2010.pdf

https://en.wikipedia.org/wiki/LouisBachelier#CITEREFBachelier1900a https://lambert-guillaume.medium.com/pricing-uniswap-v3-lp-positions-towards-a-new-options-paradigm-dce3e3b50125 https://en.wikipedia.org/wiki/Black%E2%80%93Scholesequation https://arxiv.org/abs/2103.14769 https://classic.curve.fi/files/stableswap-paper.pdf https://arxiv.org/pdf/2111.08115.pdf https://www.desmos.com/calculator/fg8a730ddz https://arxiv.org/pdf/2208.06046.pdf https://lambert-guillaume.medium.com/an-analysis-of-the-expected-value-of-the-impermanent-loss-in-uniswap-bfbfebbefed2 https://twitter.com/odtorson/status/1603337199465865216?s=46\&t=e0EQ5vcjHihnkeZ26T4eA https://en.wikipedia.org/wiki/It%C3%B4%27slemma#GeometricBrownianmotion https://scholar.google.com/scholar?q=modelling+multifractal+properties+of+cryptocurrency+markets\&hl=en\&assdt=0\&asvis=1\&oi=scholart https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2810768