LUCIDA & FALCON：マルチファクター戦略を用いて強力な暗号資産ポートフォリオを構築

著者：LUCIDA \& FALCON

前言

前回の続きとして、私たちは「多因子戦略を用いて強力な暗号資産ポートフォリオを構築する」というシリーズ記事の第一篇 - 理論基礎篇を発表しました。本篇は第二篇 - データ前処理篇です。

因子データの計算前後、また単因子の有効性をテストする前に、関連データの処理が必要です。具体的なデータ前処理には、重複値、異常値/欠損値/極端値、標準化、データ頻度の処理が含まれます。

一、重複値

データ関連定義：

• キー（ Key ）：一意のインデックスを示します。例：すべてのトークンの全日付データに対して、キーは「tokenid/contractaddress - 日付」
• 値（ Value ）：キーによってインデックスされたオブジェクトを「値」と呼びます。

重複値を診断するには、データが「あるべき」姿を理解する必要があります。通常、データの形式には以下があります：

1. 時系列データ（ Time Series ）。キーは「時間」。例：単一トークンの5年間の価格データ
2. 横断面データ（ Cross Section ）。キーは「個体」。例：2023年11月1日の暗号市場のすべてのトークンの価格データ
3. パネルデータ（ Panel ）。キーは「個体-時間」の組み合わせ。例：2019年1月1日から2023年11月1日までの4年間のすべてのトークンの価格データ。

原則：データのインデックス（キー）が決まれば、データがどのレベルで重複値がないべきかがわかります。

チェック方法：

1. pd.DataFrame.duplicated(subset=[key1, key2, …])

   重複値の数をチェック：pd.DataFrame.duplicated(subset=[key1, key2, …]).sum()

   重複サンプルを抽出：df[df.duplicated(subset=[…])].sample() サンプルを見つけた後、df.locを使ってそのインデックスに対応するすべての重複サンプルを選択します。

2. pd.merge(df1, df2, on=[key1, key2, …], indicator=True, validate='1:1')

   横方向にマージする関数にindicatorパラメータを追加すると、mergeフィールドが生成され、dfm['merge'].value_counts()を使用してマージ後の異なるソースのサンプル数をチェックできます。

   validateパラメータを追加すると、マージされたデータセットのインデックスが期待通り（1対1、1対多、または多対多）であるかを検証できます。最後のケースは実際には検証が不要です。期待と一致しない場合、マージプロセスはエラーを報告し、実行を中止します。

二、異常値/欠損値/極端値

異常値が発生する一般的な原因：

1. 極端な状況。例えば、トークン価格が0.000001ドルや時価総額が50万ドルのトークンは、少し動くだけで数十倍のリターンを得ることができます。

2. データの特性。例えば、トークン価格データが2020年1月1日からダウンロードされる場合、前日の終値がないため、2020年1月1日のリターンデータを計算することはできません。

3. データエラー。データ提供者は間違いを犯すことがあり、例えば12元のトークンを1.2元として記録することがあります。

異常値と欠損値の処理原則：

1. 削除。合理的に修正できない異常値は削除を検討できます。

2. 置換。通常、極端値の処理に使用されます。例えば、ウィンザー化（Winsorizing）や対数変換（あまり使用されません）。

3. 補完。欠損値に対しても合理的な方法で補完を検討できます。一般的な方法には、平均（または移動平均）、補間（Interpolation）、0での補完df.fillna(0)、前方df.fillna('ffill')/後方補完df.fillna('bfill')などがあります。補完に依存する仮定が合っているかを考慮する必要があります。

   機械学習では、後方補完は慎重に使用する必要があります。Look-ahead biasのリスクがあります。

極端値の処理方法：

1. パーセンタイル法。

順序を小から大に並べ、最小および最大の割合を超えるデータを臨界データに置き換えます。歴史データが豊富なデータには、この方法は比較的粗く、あまり適用されません。固定割合のデータを強制的に削除すると、一定の割合の損失を引き起こす可能性があります。

2. 3σ / 三倍標準偏差法

標準偏差σfactorは因子データの分布のばらつきを示します。μ±3×σの範囲を利用してデータセット内の異常値を識別し、約99.73%のデータがこの範囲に収まります。この方法の適用前提：因子データは正規分布に従う必要があります、すなわちX∼N(μ,σ²)。

ここで、μ=∑ⁿᵢ₌₁⋅Xi/N, σ²=∑ⁿᵢ₌₁=(xi-μ)²/n、因子値の合理的範囲は[μ−3×σ,μ+3×σ]です。

データ範囲内のすべての因子に対して以下の調整を行います：

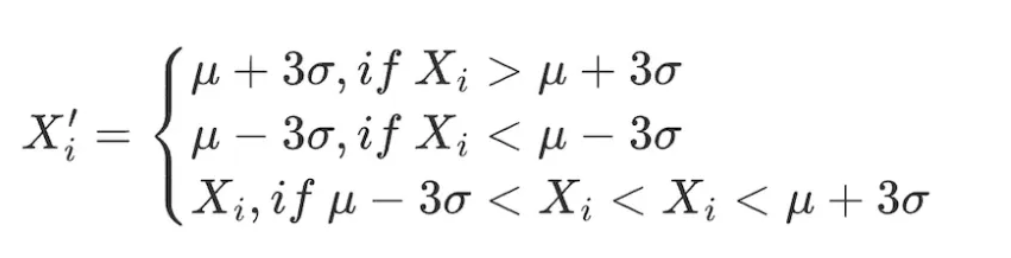この方法の欠点は、量的分野で一般的に使用されるデータ（株価、トークン価格など）が尖峰厚尾分布を示し、正規分布の仮定に合わないことです。この場合、3σ法を使用すると、多くのデータが誤って異常値として識別される可能性があります。

3. 絶対値差の中央値法（Median Absolute Deviation, MAD）

この方法は中央値と絶対偏差に基づいており、処理されたデータは極端値や異常値に対してそれほど敏感ではありません。平均と標準偏差に基づく方法よりも堅牢です。

絶対偏差値の中央値 MAD = median(∑ⁿᵢ₌₁(Xi - Xmedian))

因子値の合理的範囲は[Xmedian - n × MAD, Xmedian + n × MAD]です。データ範囲内のすべての因子に対して以下の調整を行います：

# 因子データの極端値処理
class Extreme(object):
    def __init__(s, ini_data):
        s.ini_data = ini_data

    def three_sigma(s, n=3):
        mean = s.ini_data.mean()
        std = s.ini_data.std()
        low = mean - n * std
        high = mean + n * std
        return np.clip(s.ini_data, low, high)

    def mad(s, n=3):
        median = s.ini_data.median()
        mad_median = abs(s.ini_data - median).median()
        high = median + n * mad_median
        low = median - n * mad_median
        return np.clip(s.ini_data, low, high)

    def quantile(s, l=0.025, h=0.975):
        low = s.ini_data.quantile(l)
        high = s.ini_data.quantile(h)
        return np.clip(s.ini_data, low, high)

三、標準化

1. Z - スコア標準化

• 前提：XN（μ，σ）
• 標準偏差を使用しているため、この方法はデータ内の異常値に対して敏感です。

x'ᵢ=(x−μ)/σ=(X−mean(X))/std(X)

2. 最大最小値差標準化（Min - Max Scaling）

各因子データを(0,1)の範囲のデータに変換し、異なる規模や範囲のデータを比較できるようにしますが、データ内部の分布を変更することはなく、合計を1にすることもありません。

• 極大極小値を考慮するため、異常値に敏感です。
• 単位を統一し、異なる次元のデータを比較しやすくします。

x'ᵢ=(xᵢ−min(x))/(max(x)−min(x))

3. 順位パーセンタイル（Rank Scaling）

データの特徴をその順位に変換し、これらの順位を0と1の間のスコアに変換します。通常はデータセット内のパーセンタイルです。*

• 順位は異常値の影響を受けないため、この方法は異常値に敏感ではありません。

• データ内の各点間の絶対距離を保持せず、相対的な順位に変換します。

NormRankᵢ=(Rankₓᵢ−min(Rankₓᵢ))/(max(Rankₓ)−min(Rankₓ))=Rankₓᵢ/N

ここで、min(Rankₓ)=0、Nは範囲内のデータポイントの総数です。

# 因子データの標準化
class Scale(object):
    def __init__(s, ini_data, date):
        s.ini_data = ini_data
        s.date = date

    def zscore(s):
        mean = s.ini_data.mean()
        std = s.ini_data.std()
        return s.ini_data.sub(mean).div(std)

    def maxmin(s):
        min = s.ini_data.min()
        max = s.ini_data.max()
        return s.ini_data.sub(min).div(max - min)

    def normRank(s):
        # 指定された列の順位を計算します。method='min'は同じ値が同じ順位を持つことを意味し、平均順位にはなりません。
        ranks = s.ini_data.rank(method='min') 
        return ranks.div(ranks.max())

四、データ頻度

時には得られたデータが私たちの分析に必要な頻度ではありません。例えば、分析のレベルが月次で、元のデータの頻度が日次の場合、この時「ダウンサンプリング」を使用してデータを月次に集約する必要があります。

ダウンサンプリング

これは集合内のデータを1行のデータに集約することを指します。例えば、日次データを月次に集約します。この時、集約される指標の特性を考慮する必要があります。一般的な操作には以下があります：

• 最初の値/最後の値
• 平均/中央値
• 標準偏差

アップサンプリング

これは1行のデータを複数行のデータに分割することを指します。例えば、年次データを月次分析に使用します。この場合、単純に繰り返すだけで済むことが多く、時には年次データを各月に比例して集約する必要があります。

LUCIDA \& FALCONについて

Lucida（https://www.lucida.fund/）は業界をリードする量的ヘッジファンドで、2018年4月にCrypto市場に参入し、主にCTA / 統計的アービトラージ / オプションボラティリティアービトラージなどの戦略を取引しています。現在、管理規模は3000万ドルです。

Falcon（https://falcon.lucida.fund /）は新世代のWeb3投資インフラであり、多因子モデルに基づいてユーザーが暗号資産を「選択」、「購入」、「管理」、「販売」するのを支援します。Falconは2022年6月にLucidaによって孵化されました。

詳細はhttps://linktr.ee/lucida_and_falconをご覧ください。