Uniswap v3 Mathematical Insights: How Options Combine with Positions

Written by: ck.eth

Compiled by: Lylia, Antalpha Labs

The original series consists of six parts, this is the fifth part, which continues to introduce how options can be combined with positions. A certain understanding of the position strategies discussed in the previous parts of this series is required. To make useful information about Uniswap V3 more accessible and understandable, we have translated the series of articles to provide Chinese readers with a deeper understanding of the Uniswap v3 mechanism and investment strategy choices. While reading this translation, you can refer to the original text for more detailed information at any time.

Non-linear risk of Uniswap yield convexity / Theta-Gamma volatility. https://www.math3d.org/WvsEXvTWD

In short:

• Showcased Greek solutions for Uniswap v2 and v3
• Provided solutions for hedging Asian options, European options, and Bachelier options using Uniswapv3 in an interactive desmos file.
• Demonstrated LP hedging accumulation strategies using desmos.
• Explained the history and alternative derivations leading to LVR.

Greek Parameters - Uniswap v2

Instead of allocating 100% to the LP position, it is better to allocate part to asset X and use the remaining part to short asset X to reduce but not eliminate divergence losses. The result is to transform the payment structure from a cliff to a hill, as shown by Guillaume Lambert: Greek parameters inform us of the sensitivity of the LP position's value relative to another variable (e.g., time, volatility, and interest rates). We introduced Delta and Gamma in Part 4. LP Greek parameters are useful because you can match them with the Greek parameters of options to offset price discrepancies, such as the effects when prices fluctuate, volatility changes, or time passes, namely delta and gamma. The numerical values of the Greek parameters tell us the impact of various factors on the LP position price.

Interactive desmos file for v2: https://www.desmos.com/calculator/inwy6djhhm

It is important to note that compared to options, the Greek parameters of Uniswap tend to infinity when the LP position price drops, as indicated by the dashed line at x=0 in the above figure. To cut these tail risks, we can use concentrated ranges in v3.

Greek Parameters - Concentrated LP Range v3

Desmos file for univ3 Greek parameters: https://www.desmos.com/calculator/l8sqzlwkf5

The smaller we concentrate the range pa (lower limit) ~ pb (upper limit), the more sensitive our Delta Δ and Gamma Γ become, noting that Gamma is negative, which means our LP payments have a concave black shape. Our theta /Θ / expected costs will also increase, while interest rate sensitivity ρ is essentially unaffected.

However, while the payment graph of a single LP position may match that of an option, other Greek parameters may not match.

LP Greek parameters do not look like conventional options: https://www.desmos.com/calculator/nyuw7sybin

Here, we have a call option for a single LP range, but other Greek parameters are not fixed.

A useful trick is that instead of trying to find a way to hedge the LP position, one first needs to find an option in the market with a strike price (K) as well as implied volatility (σ_iv) and expiration time (t). After that, a series of LP positions can be constructed that follow a log-normal distribution, initially inspired by Dan Robinson's normal distribution liquidity fingerprint for Uniswap v3 ^[1]^. The granularity of LP positions matching the log-normal distribution in price space allows for smoothing of the Greek parameters:

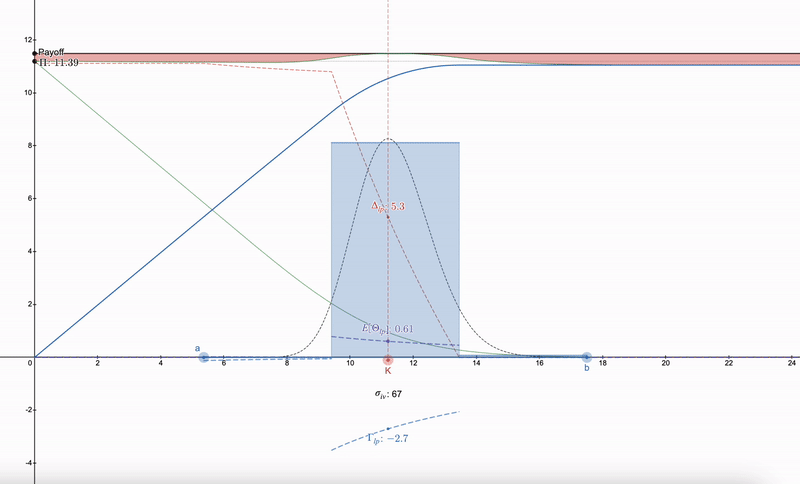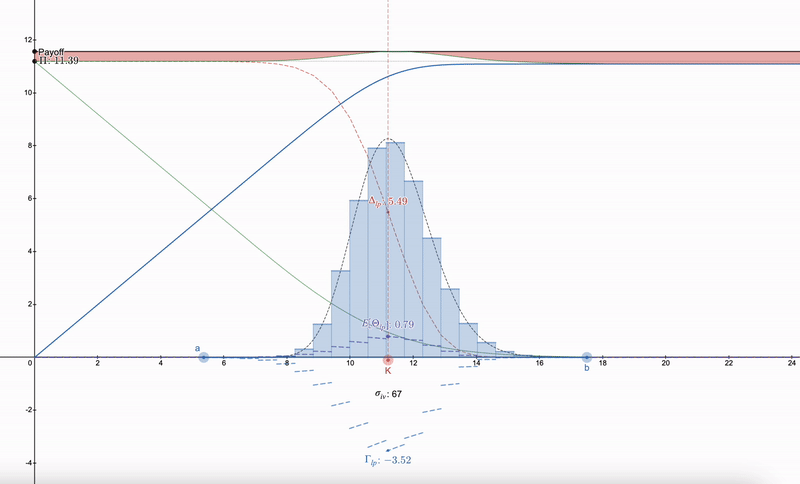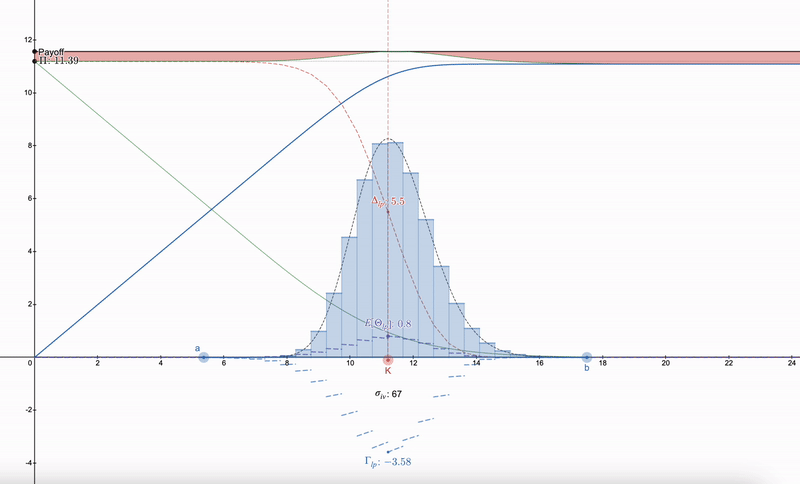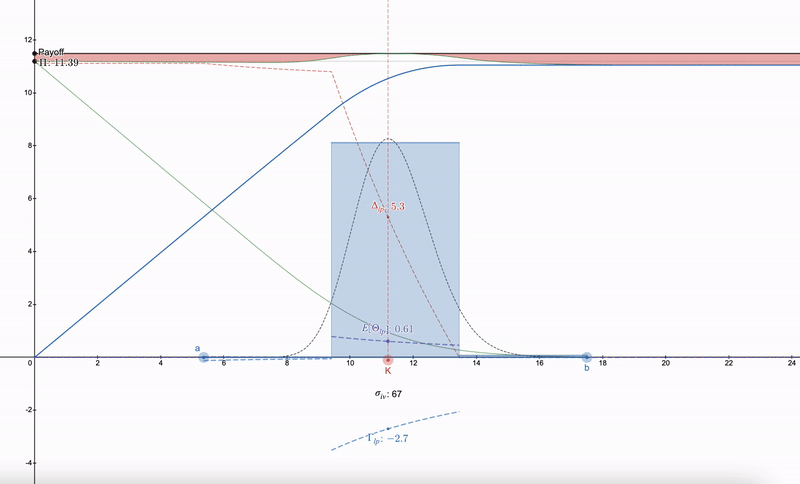
Note that LP Greeks start to resemble options. As prices drop, the diversity of LP positions allows one to switch to the next range. More than 7 LP positions will lead to diminishing returns.

Interestingly, it seems very difficult to completely cancel payments using a log-normal distribution (please correct me if I'm wrong), but if the log-normal liquidity fingerprint approaches the Dirac Delta function, the aforementioned differences (visualized in red in the above figure) will disappear. For example, Asian options also follow a log-normal distribution, but surprisingly, they are more sensitive to price, with Δ and Γ being sharper, as the volatility of Asian options is 1/√3 of that of conventional options, thus having a smaller impact on payment discrepancies:

Using European put options to hedge LP position combinations to hedge with their equivalent Asian put options.

A single LP position can roughly match a European option but will ignore the smoothed Greek parameters, while a series of LP positions will smooth the Greek letters but leave a hill. This trade-off may be improved in the future through potential adjustments/skewed liquidity fingerprints.

LP Hedging Strategies

On the other hand, if one is not interested in trying to cancel concave LP payments, then the desmos file: https://www.desmos.com/calculator/khvbqzncg9 can also be used to see how various payment methods work. Below is an example of a series of payments that may occur.

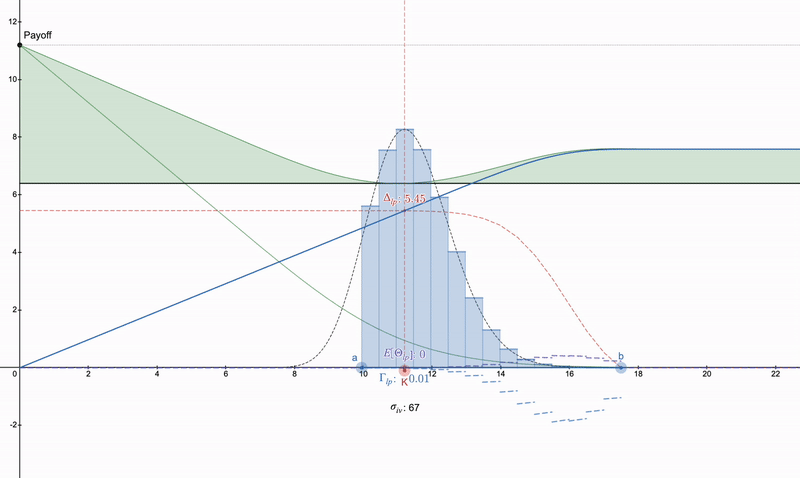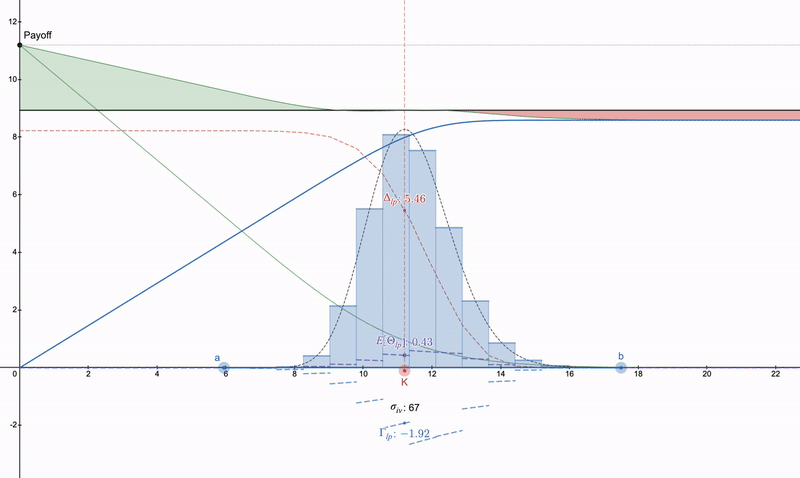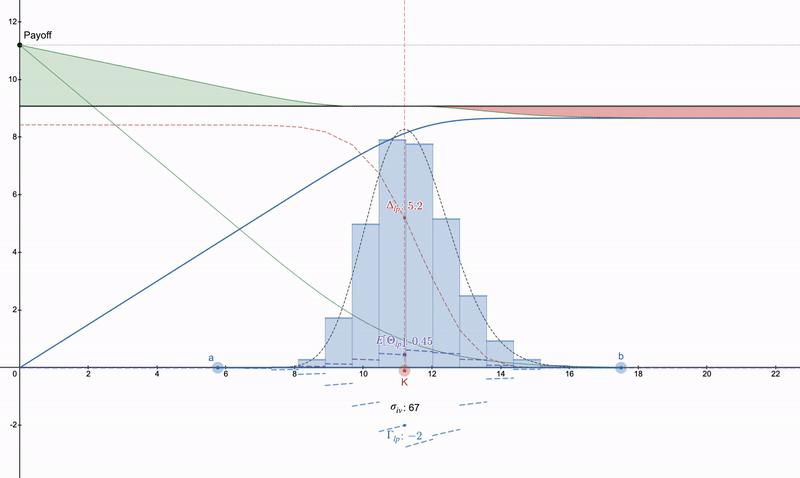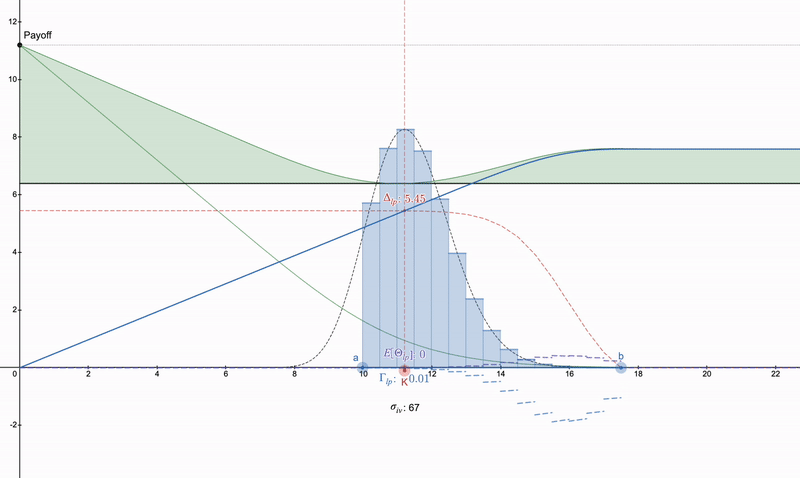
Vertical put spread >> put option >> some long straddle. Note that due to theta decay, put options will intensify over time, while LP positions can grow due to fees.

I noticed an interesting feature of v3: if liquidity is concentrated at exactly 75% or lower of the current price for pa and pb is set to the current price, the value of asset X peaks at 25%, which may have strategic value for those trying to accumulate assets.

Dan Robinson's v3 tool: https://twitter.com/danrobinson/status/1430678225945042945

Such a single range can be combined with market put options to achieve the following payments: https://www.desmos.com/calculator/a8y3pl3t03:

Put option parameters can be extracted from the market. Over time, if the price does not drop fast enough, the value of the options will decrease.

Such a strategy is essentially aimed at seeking a price drop to accumulate assets in the future and earn fees. It is important to note that without options, this would become a riskier approach and only makes sense if the executor has a very strong belief in the asset's rebound. However, please note that this does not constitute any financial advice; I am merely doing mathematical calculations.

Historical Deep Dive Leading to LVR:

In Part 4, I pointed out the relationship between the concavity of LP positions and returns, and hoped to expand on this from the perspective of history and LP divergence losses/losses with rebalancing (LVR).

Taleb pointed out that the first person to write about the non-linear relationship between risk and return was Louis Bachelier ^[2]^ in the 1900 Theory de la Speculation ^[3]^, attributing it to its similarity to Fourier's heat equation. Coincidentally, Lambert used the Feynman-Kac method to solve the value of concentrated LP positions ^[4]^.

Page 46 of "Theory de la Speculation". A constant is squared, a dt and a dx²!

Bachelier's equation is just a slightly rearranged Black-Scholes-Merton equation with the drift rate set to zero ^[5]^.

The change in asset prices over time is related to volatility and curvature.

LHS is theta-Θ, RHS is curvature gamma Γ, which is concave due to the negative sign. Then, zero Angeris, Evans, and Chitra ^[6]^ pointed out that the LP positions of AMMs must have concave payment functions. From Curve's CSMM ^[7]^ to Forgy & Lau ^[8], the entire symmetric liquidity curve space should be concave for all LPs.

According to the concavity equality in our right-side equation, this means that the market maker (LP) positions themselves must have a premium. Without a premium, the equality below would be violated, and one could simply borrow such an LP position and buy part of the underlying asset to construct a perpetual long straddle and wait to capitalize on the increase in volatility.

Bachelier equivalence / BSM dynamic hedging - referred to as concave command returns, while convex command costs. Mathematically expressed:

Returns ∝ Risk times concavity (negative convexity). BK derivation in the appendix.

In solving the Theta Greek value of Uniswap ^[9]^, I noticed that by substituting the second derivative of the LP position into the above formula, one can obtain the same equation as LVR ^[10]^.

Formula 16. If Gamma in the Bachelier equivalence is -L/2sqrt(x)³, the same result will be obtained.

LVR paper Figure 2 derives the vol²/8 LVR relationship from the above invariant xy=k figure, which leads to concave LP returns.

This is no coincidence; people from different angles have arrived at the same conclusion. Lambert actually included the drift rate ^[11], while others excluded it ^[12].

Please note that all these models assume a Gaussian distribution, originally stemming from Brownian motion (BM) in Itô's lemma ^[13], which gives us the internal -σ²/2 term that also appears in Angeris, Evans, and Chitra's final equation ^[6], but we know that digital assets, including stablecoins, exhibit a Hurst index >0.5, implying fractal BM behavior ^[14], and Sepp and Rakhmonov also pointed out that stochastic volatility methods apply to the skewed implied volatility structure of digital assets ^[15].

By examining the tail returns of the log-log histogram of the most persistent digital assets, we also see non-Gaussian tails.

BTC-USD histogram returns smoothed by kernel density shown in blue

Given the shape of the histogram, we will have to delve into the uniform distribution of the full range of Uniswap v2 and go beyond the Gaussian cliff to gain insights into the leverage (LVR) theta values suitable for market makers.

Log-log histogram of 50+ distributions. Exponential laws and power laws await us in the abyss.

Appendix:

Bachelier equivalence derivation.

LVR of Uniswap LP positions derived from Bachelier equivalence.

References:

https://www.desmos.com/calculator/l1oivvaptt

https://www.maths.usyd.edu.au/u/UG/SM/MATH3075/r/HaugTaleb2010.pdf

https://en.wikipedia.org/wiki/LouisBachelier#CITEREFBachelier1900a https://lambert-guillaume.medium.com/pricing-uniswap-v3-lp-positions-towards-a-new-options-paradigm-dce3e3b50125 https://en.wikipedia.org/wiki/Black%E2%80%93Scholesequation https://arxiv.org/abs/2103.14769 https://classic.curve.fi/files/stableswap-paper.pdf https://arxiv.org/pdf/2111.08115.pdf https://www.desmos.com/calculator/fg8a730ddz https://arxiv.org/pdf/2208.06046.pdf https://lambert-guillaume.medium.com/an-analysis-of-the-expected-value-of-the-impermanent-loss-in-uniswap-bfbfebbefed2 https://twitter.com/odtorson/status/1603337199465865216?s=46\&t=e0EQ5vcjHihnkeZ26T4eA https://en.wikipedia.org/wiki/It%C3%B4%27slemma#GeometricBrownianmotion https://scholar.google.com/scholar?q=modelling+multifractal+properties+of+cryptocurrency+markets\&hl=en\&assdt=0\&asvis=1\&oi=scholart https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2810768