Understanding Encrypted Memory Pools: A New Design Space for Solving MEV and Censorship Issues

Original Title: 《Encrypted Mempools》

Original Author: Jon Charbonneau

Compiled by: 0x11, Foresight News

Encrypted mempools are a powerful tool for addressing MEV and censorship issues, with various standalone solutions already available that can also be combined.

This article outlines the design space built around the topic from Justin Drake's talks (Columbia, Amsterdam, and Flashbots Roast). Most of you may find it difficult to understand on the first viewing, so I will try to break it down and expand on it simply.

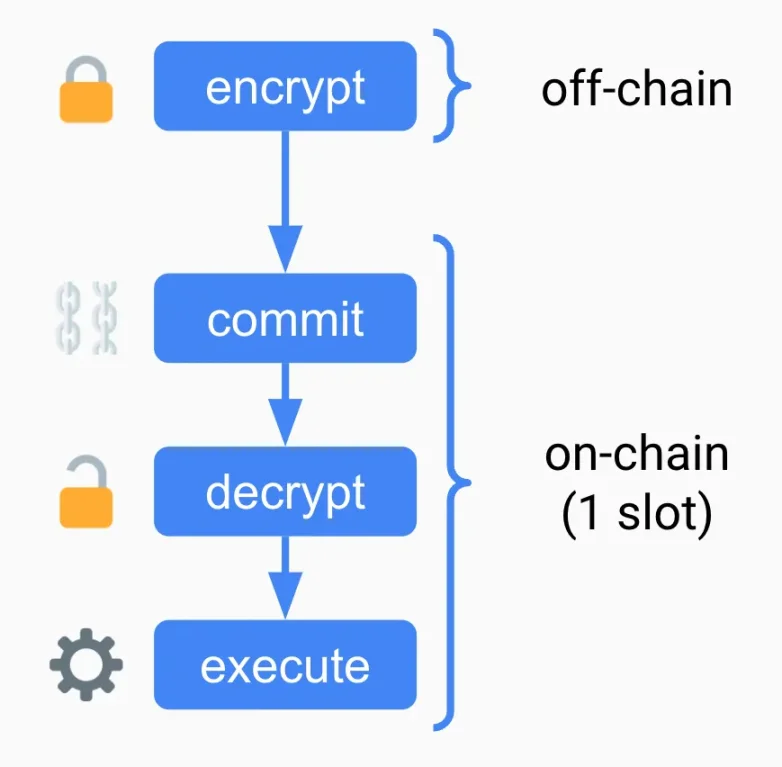
The basic idea: allow users to submit encrypted transactions, which can only be decrypted by block producers:

• Users encrypt and broadcast transactions
• Encrypted transactions are submitted
• Transactions are decrypted
• Transactions are executed (Note: submission, decryption, and execution may occur in a single slot)

Two problems seem to be easily solvable:

• MEV: If I can't see it, I can't front-run the transaction
• Censorship: I can't censor transactions unless I exclude all encrypted transactions (if many transactions are encrypted, the cost may be very high)

One key point that needs to be ensured is that decryption does not depend on the user. There are several ways to achieve this:

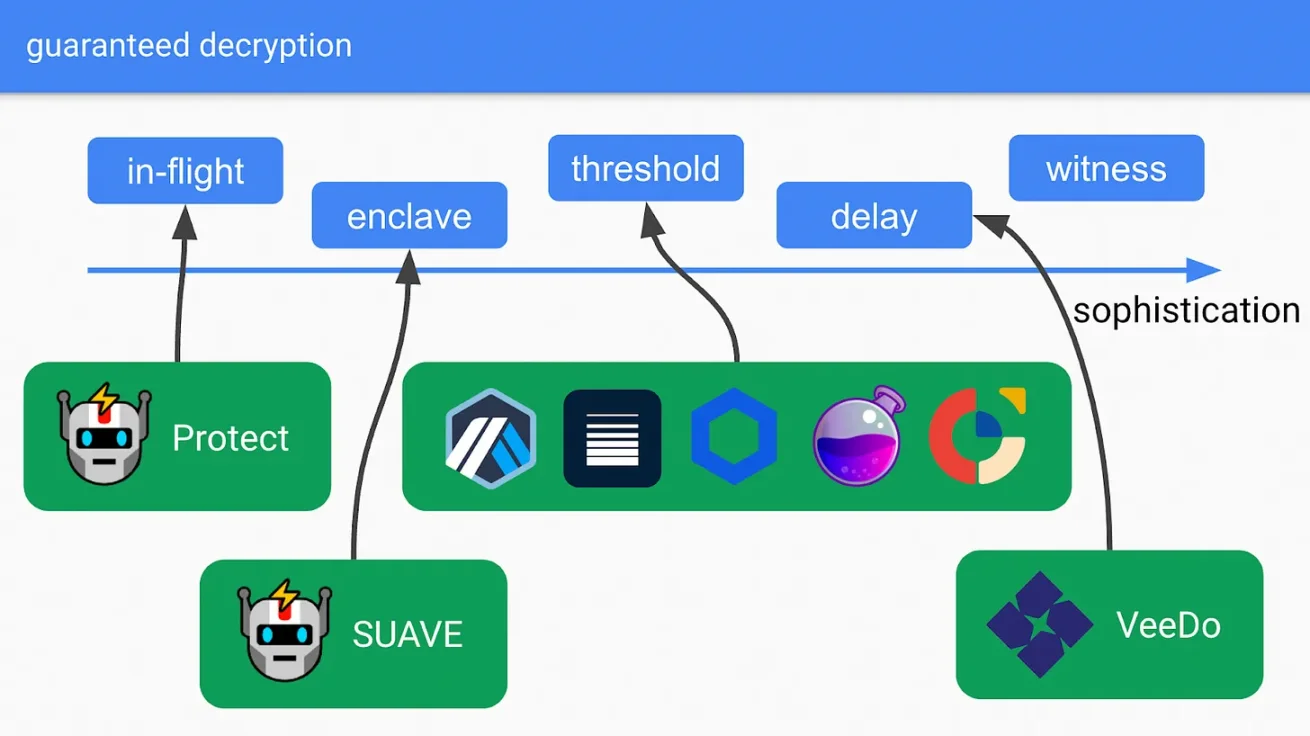
1. In-flight

Trust a third party, send data to them privately, they can decrypt and view the data but promise not to disclose it publicly before the data is submitted to the chain. This is how products like Flashbots Protect work.

2. Trusted Hardware

You can utilize trusted hardware. The plaintext can run in trusted hardware but will not be publicly decrypted before the transaction is submitted. The most famous example is Flashbots SUAVE's SGX.

3. Threshold Encryption/Decryption (TED)

A committee can come together to force the decryption of ciphertext, but a threshold of signers is required to do so. For example, your "threshold" might require 2/3 of validators to agree to decrypt. TED has been researched in several different areas, including:

• Ethereum L1 ------ Shutterized Beacon Chain
• Shutter Network ------ Ethereum L2s
• Arbitrum ------ Chainlink's FSS
• Osmosis & Anoma ------ Ferveo

Shutterized Beacon Chain

Taking a closer look at the Shutterized Beacon Chain proposal, a subset of validators ("keypers") generates a public/private key pair using a distributed key generator (DKG). Everyone can see the public key, but the private key is split into multiple shares held within the committee. Reconstructing the private key and decrypting requires a certain threshold of key shares (e.g., 2/3).

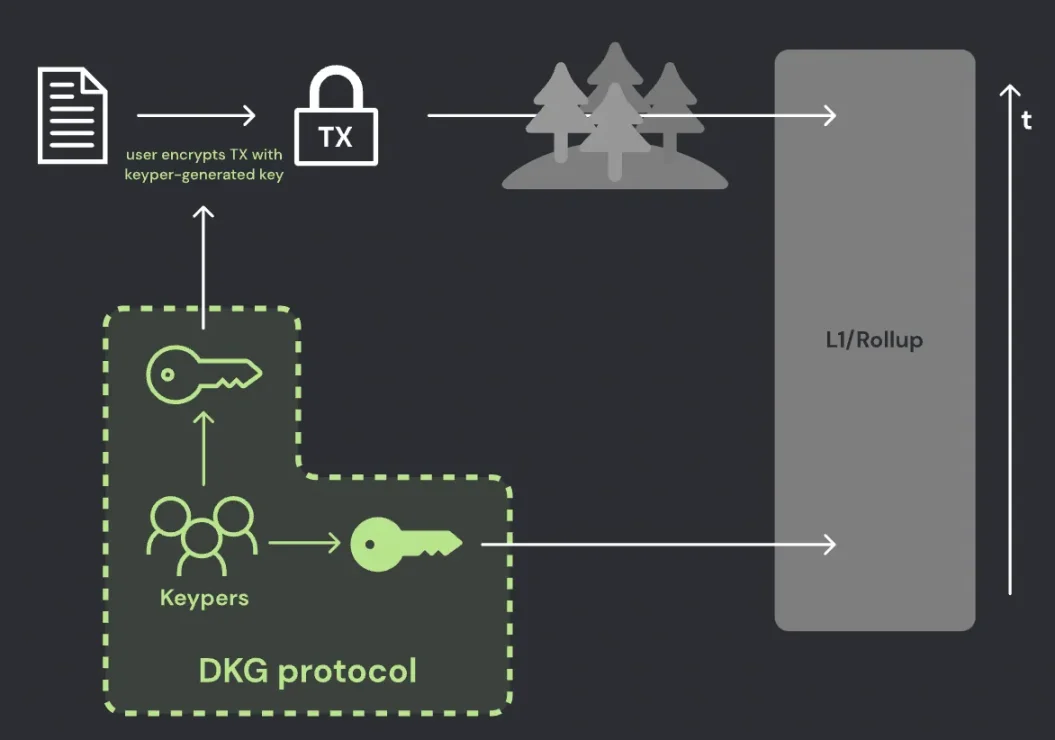
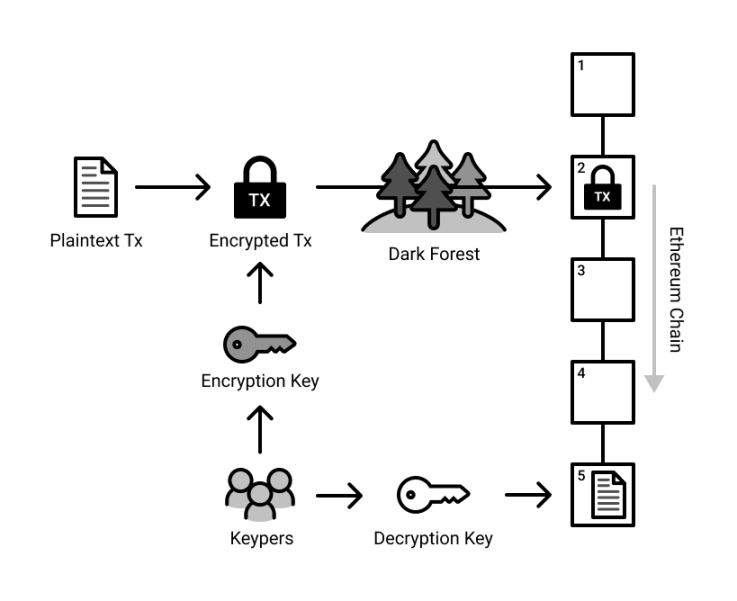
Users can optionally encrypt transactions, which are included on-chain before their contents are decrypted and executed. Block producers create blocks using plaintext transactions (executed immediately) and encrypted transactions (scheduled for future block heights).

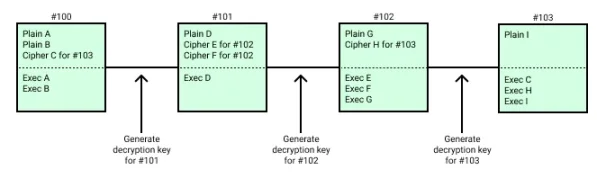
After generating and proving block n -1, keypers should generate and publish the decryption key for block n. This key can decrypt the transactions within block n. Block n must contain the decryption key to be considered valid. The post-state of the block is calculated as follows: execute the encrypted transactions in the block before executing the plaintext transactions (in the order they are set).

Disadvantages

TED has several disadvantages:

Lack of Accountability: Unlike traditional security assumptions, malicious behavior here is untraceable or unreportable. Keypers can decrypt immediately, and you cannot attribute it. Even if you assume that validators' behavior is incentive-compatible, three-letter agencies outside the validator set may exert influence on them.

Honest Majority Assumption: A dishonest committee may cause issues, such as choosing to never decrypt certain messages or secretly decrypting messages they shouldn't (e.g., at the request of government agencies or selfishly extracting MEV). In most cases, blockchains rely on a majority that is economically rational (i.e., the penalties for being slashed usually outweigh the economic incentives for malicious double-spending, etc.). With threshold encryption, this assumption is shifted to a truly honest and selfless majority.

Destabilization of Protocol: Essentially a combination of the above two points, TED increases the incentive for validators to act maliciously and is not easily punishable.

Reduced Liveliness: A higher decryption threshold enhances the security of the protocol. However, this directly undermines liveliness. For example, a large-scale network interruption could cause half of the validators to go offline, potentially halting the protocol. This is an unacceptable trade-off, especially for Ethereum, which places a strong emphasis on "third-world war" liveliness.

Poor User Experience: TED may introduce varying degrees of latency and costs depending on implementation details.

Suboptimal Value Distribution: Let's look at a simple front-running example:

• 1 ETH priced at $1000
• If I send the transaction to the vanilla mempool ------ I get $990 (the seeker front-runs and back-runs, netting $10)
• If I send the transaction to the TED mempool ------ I get $995 (the seeker cannot front-run, but I push the local spot price, creating a $5 arbitrage opportunity for the seeker)
• I send the transaction to the best order flow auction ------ I get $1000 (I do not get front-runs or back-runs. Or similarly, I do get front-runs and/or back-runs, but the seeker must bid $10 in a competitive auction to gain the right to do so, resulting in the same outcome.)

In this case, you leave money on the table for others to take. An economically rational user should publicly disclose enough order information so they can receive compensation close to the full value of the order. They should not naively threshold encrypt their transactions, hiding the value it provides (allowing others to capture it).

This is an overly idealized example, but you get the point; covering up problems does not always solve them. TED can be a useful tool, but it is not a panacea for MEV. In some cases, CR may be better.

Additionally, Ethereum introduces extra complexity. For instance, its lack of instant finality (though this may change one day with single-slot finality) introduces issues around reorganization. I believe that at least in Ethereum's L1, the trade-offs here are more beneficial than harmful. Increasing Ethereum's trust assumptions, increasing the incentives for collusion (to go undetected), and the damage caused by reducing its liveliness may outweigh the benefits.

However, some of these trade-offs may be more acceptable for L2 or other L1s compared to Ethereum L1.

4. Delayed Encryption/Decryption (DED)

With delayed encryption, you can set encrypted information to automatically decrypt after a certain period, which is related to sequential computation with VDF.

To actually implement DED, you need VDF ASICs. Fortunately, the Ethereum Foundation and Protocol Labs have been working on building them and recently received the first batch of test samples of chips built by GlobalFoundries. These VDF evaluators should be capable of performing extremely fast sequential computations. These VDF ASICs are also applicable for time-lock puzzles and DED.

VDF also needs to generate SNARKs. This can be done using GPUs, but ideally, the Ethereum Foundation also hopes to produce ASICs related to SNARK production.

Overall, you no longer trust a committee, so the usual preferred security assumption applies. However, requiring specialized hardware is not ideal, and the required delay may also increase the latency of the system. Interestingly, you can combine the advantages of TED + DED…

5. Witness Encryption/Decryption (WED)

WED is powerful, but don't get too excited; it won't arrive quickly. This is a very peculiar thing and will take many years to realize. But it's cool and helps with understanding, so I will briefly introduce it.

WED allows any witness to force the decryption of ciphertext. For example, your rule could be "only decrypt after Ethereum has completed including a block with the encrypted payload," and it will only decrypt in the case of proving this. You can imagine any complex statement you want to implement requiring SNARK.

WED is essentially a generalization of TED or DED. You can even build a hybrid of both. For example, a designated witness can prove:

• Happy outcome: the threshold committee has signed off on decryption, or
• Backup plan: the required time has passed, returning for delayed decryption

This provides a backup in case the threshold committee does not respond. It also allows you to be more conservative when parameterizing m/n threshold assumptions (i.e., you can require every committee member or almost all members to sign).

• Happy outcome: best user experience, the entire committee confirms instantly
• Backup plan: delays and UX are temporarily affected, but liveliness is preserved

In practice, WED could verify any statement you want with SNARK. For example:

• TED: you could have a SNARK to prove "I have m out of n signatures" to force decryption.
• DED: you could use VDF and perform sequential computation (which is very expensive). Then at the end of your computation, you have a short proof. Then you take that short proof and wrap it in a SNARK (to make it shorter) and input it to force decryption.

Homomorphic

In each of the encryption schemes here (threshold, delayed, and witness), you can have homomorphic properties. That is, you can create threshold FHE, delayed FHE, and witness FHE schemes to perform arbitrary operations on ciphertext.

In-flight and trusted hardware solutions (e.g., SGX) can also simulate the same functionality ------ operating on private data. This is because in both cases, the trusted third party or hardware can access the plaintext itself for operations. However, ideally, we want to remove these trust assumptions and rely solely on strengthened cryptography.

We can imagine an example:

• m1 = transaction 1
• m2 = transaction 2
• f(x) = build a block

Then all five solutions can replicate the following functionality:

When considering how to hide transaction metadata and use encrypted inputs to build the best block, keep this capability in mind. Theoretically, each of the five options here could be used for solutions that require "homomorphic."

Metadata

Metadata is data that provides information about other data but does not provide the content of that data (e.g., the text of a message or the image itself). For our purposes, transaction metadata can include the sender's IP address, nonce, gas payment, etc.

Ideally, we want to hide as much metadata as possible. Otherwise, it may leak information, allowing outsiders to infer your transactions (potentially providing them with enough information to attempt front-running or censorship, etc.). However, we need metadata to verify whether a transaction is valid, whether the necessary fees have been paid, whether it is spam, etc.

Let's look at some solutions for masking various metadata.

1. IP Address - Tor

Very simple ------ people can use services like Tor to privately broadcast and mask their IP addresses.

2. Signature - SNARK

You need to know at the p2p level that the encrypted transaction is valid, especially that it has a valid signature. We can use SNARK to prove the signature is valid, which will accompany each encrypted transaction. A SNARK consists of three important parts:

The user wants to prove that their transaction ciphertext is valid, corresponding to the transaction plaintext, and that its signature is valid. To prove any signature is valid, you need the public key associated with the account to verify it.

• Look up the Ethereum state root (public).
• Provide a Merkle proof of the sender's public key corresponding to this state root (private).
• Verify the signature; you need to verify the sender's public key Merkle proof based on the state root. Use SNARK to prove that your sender's public key Merkle proof is valid and that your signature is valid.

3. Gas Payment ------ SNARK

You need to prove that the sender of the encrypted transaction has enough ETH to pay for the fee. We can use SNARK again.

This is a similar process, but now you provide a Merkle path to the state root, proving the sender's balance (rather than the sender's public key). You verify the Merkle path and check if the balance is sufficient to pay the required gas.

The minimum gas required to execute basic operations such as deserializing the transaction, checking its balance, and verifying the signature. You can stipulate that the sender must always pay this minimum amount.

However, at execution time, you also need the gas limit of the actual transaction itself, which can also be encrypted. So when you go to actually execute the transaction itself, you will check if the sender has enough balance to pay for the full gas of the transaction at that time:

• If yes: run the transaction and issue a refund at the end
• If no: abort the transaction, and the sender only pays 21000 gas

4. Sender and Nonce - SNARK

Nonce is a value that equals the number of transactions sent from an address (or the number of contracts created by an account). A user's nonce starts at zero and increments by 1 with each transaction they send from their address.

One reason we have nonces today is that users cannot spam the mempool (DoS attack) with a large number of transactions to increase the likelihood of their transaction being executed. Nodes will only look at one transaction with that nonce and discard others.

For encrypted transactions, you will prove via SNARK that its nonce is the previous nonce + 1. However, if nodes can no longer discern that many encrypted transactions have the same nonce, the aforementioned DoS attack may have adverse effects.

To retain this anti-DoS property, we want to add a "replay tag." It uniquely tags the transaction so that you cannot send a large number of transaction spams for one address. To create this tag, you can simply hash (nonce, private key). Since both the nonce and private key are fixed, if a user tries to send two different transactions using the same nonce and private key, they will have the same replay tag.

Finally, you may want to retain some degree of flexibility. Suppose the gas price has fluctuated, and you have reason to want to rebroadcast the transaction at a higher price. To mitigate this, you can hash (nonce, private key, slot). Now, you can adjust your transaction once per slot, allowing each address to send one transaction per slot.

5. Data Size - Homomorphic

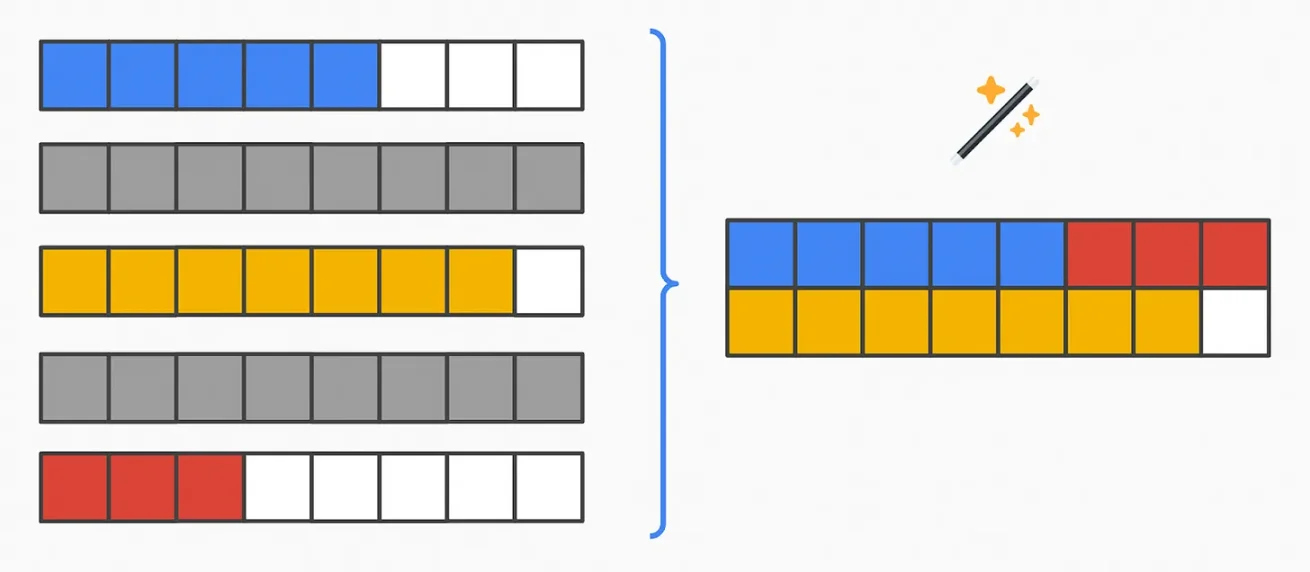
The size of encrypted data of size n in plaintext will create ciphertext of size n. Even this size is sufficient to probabilistically compute certain transactions. We can mitigate this issue by "padding" ------ adding 0s to the plaintext before encryption, expanding the bit length to the next power of 2 (e.g., adding three 0s to a 5-bit ciphertext).

In the following example:

• White = padded 0
• Other colors = actual transaction data

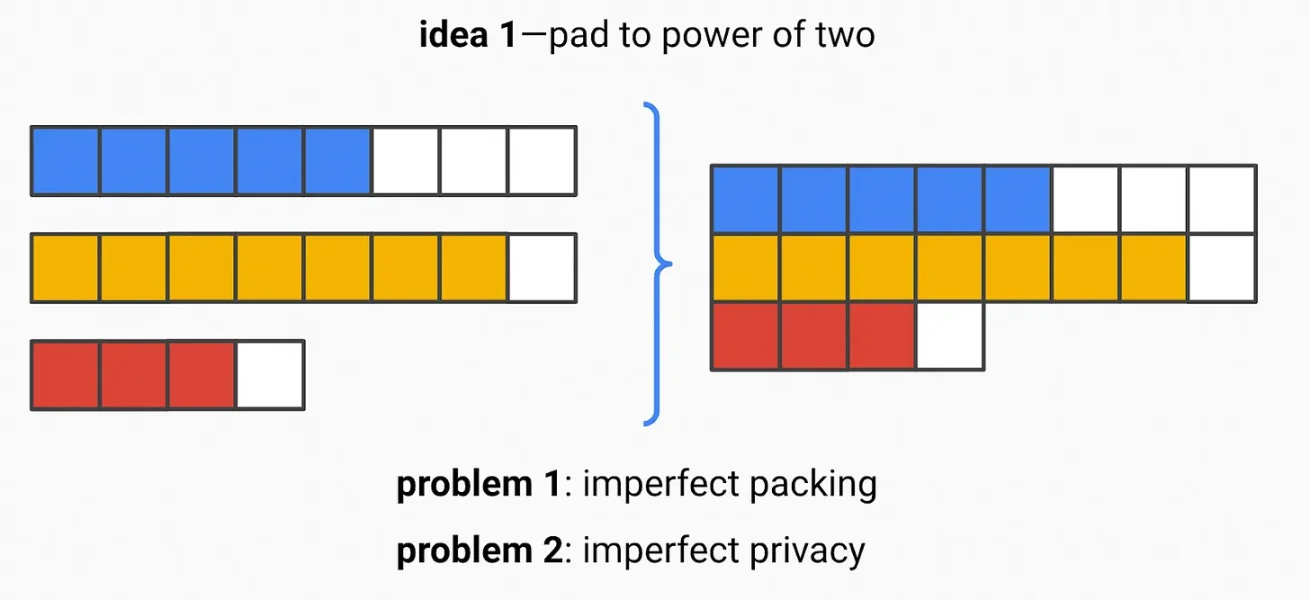
When you build a block, you can connect these ciphertexts, but this has two issues:

• Imperfect packing ------ extra 0s mean you have to pay for additional data availability
• Imperfect privacy - perhaps the power of 2 provides enough information. The distribution of transaction sizes is unclear, so certain sizes may still probabilistically reveal enough information.

A better solution involves "trimming" the padding:

• Pad each transaction to the maximum size (here 16) and homomorphically encrypt
• Apply a function on the ciphertext to effectively pack the plaintext, removing unnecessary padding

Now you achieve optimal packing.

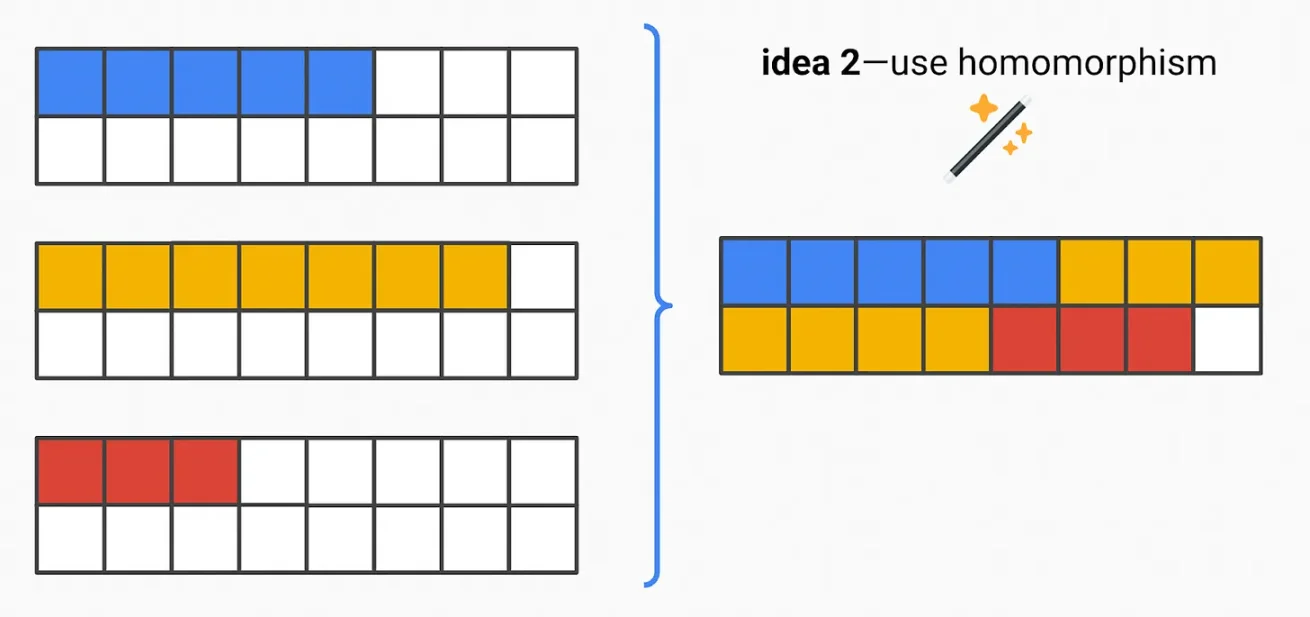
By padding to the "maximum" size, this can effectively set the maximum value to the value converted from the actual block size limit (i.e., if 30mm gas converts to approximately x kB). This means padding each transaction to a size of x kB. Or, if 99.9% of transactions typically fall within y kB, you can set a smaller, more practical size of y kB.

Similarly, trusted hardware can be used instead of the previously discussed FHE to simulate this "trimming." For example, you can run SGX and receive encrypted transactions into your trusted enclave. Within the enclave, plaintext operations can be performed on the data to trim unnecessary padding for dense block packing. Then the data is encrypted and sent back, followed by a forced decryption method (threshold, delayed, witness).

Note that in any case, the output should be of a fixed size, so you may leave a small amount of padding.

Transaction Packing Selection: Homomorphic and Disjoint State Access Lists

Assuming we have solved all the above issues, can block producers optimally pack everything economically based on size? We want to decentralize block building without losing value. Otherwise, it cannot compete with centralized entities.

Solution 1 - FHE EVM

The direct answer: run the EVM entirely in FHE. This would allow decentralized building of the optimal block, maximizing value for block producers. They choose and order transactions to maximize value.

Unfortunately, this is not a simple task. The biggest cost of FHE circuits is their "depth" (i.e., the number of gates in the longest path). In particular, its multiplication depth is very important. For example, the transaction "trimming" described earlier is a relatively "shallow" circuit (i.e., it is very simple). With hardware acceleration, such use cases may become computationally feasible in 2-3 years.

However, running the entire EVM using FHE requires very deep and complex circuits. We are finally starting to make some meaningful progress in zkEVM circuits (which are several orders of magnitude more computationally intensive than running a standard EVM), but FHE EVM is even further away.

Again, note that simulating this functionality using trusted hardware is also feasible (e.g., SGX in SUAVE does this).

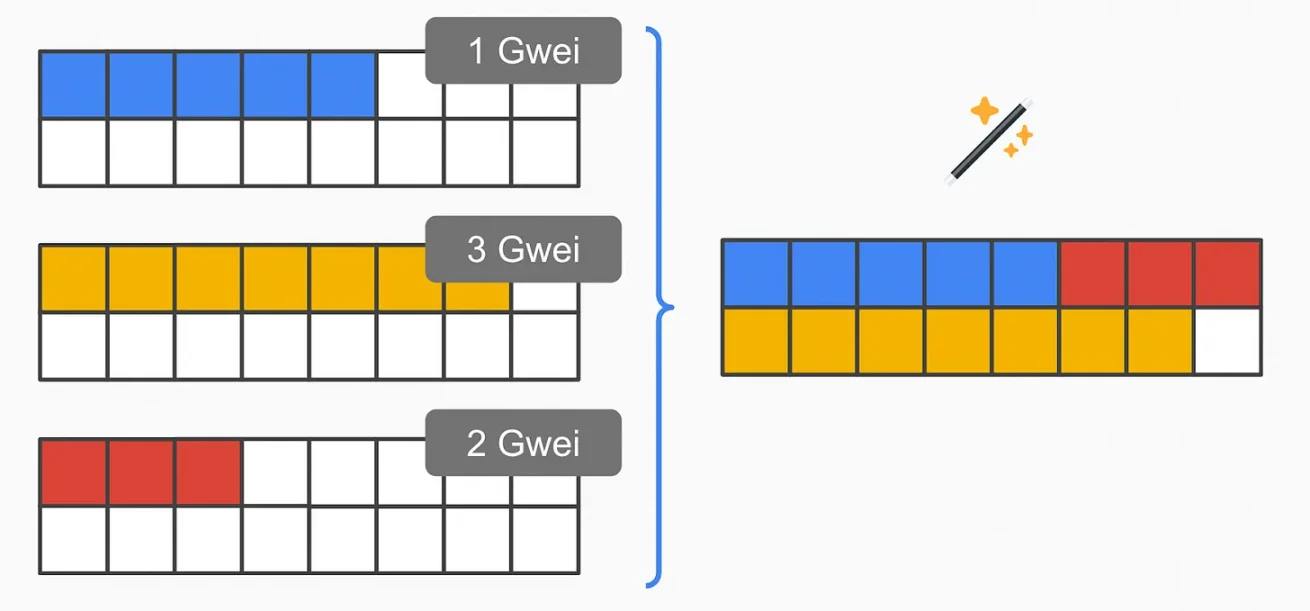
Solution 2 - State Access Lists

Alternatively, we can use FHE and access lists more limitedly. This is easier to implement than running a full FHE EVM ------ it is a shallower circuit. In this setup, the transaction pack can include an encrypted state access list and its bids. This precisely specifies which part of the state their pack will access.

Now, the homomorphic circuit for block producers only needs to pick the highest bid for transaction packs with disjoint state access lists.

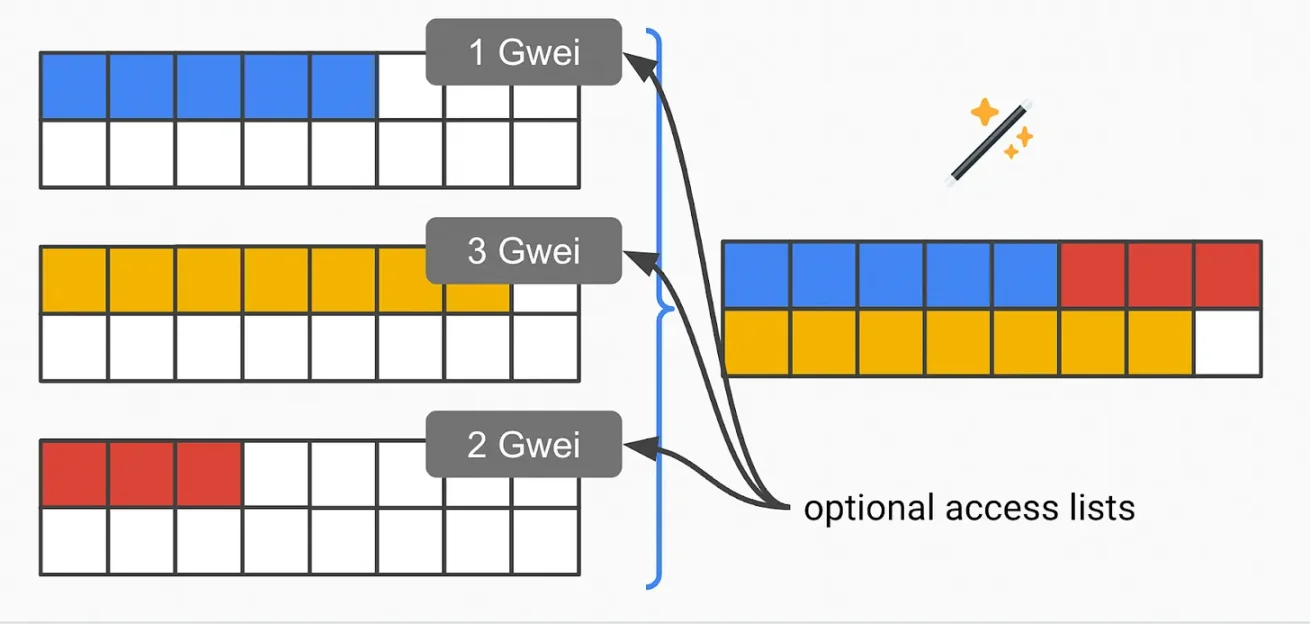
Note that this is not strictly optimal. For example, the second-highest bid (T2) in a block may access the exact same state as the highest bid (T1). In this access list example, the block producer would discard the second transaction. However, it is possible that both T1 and T2 are valid. In that case, FHE EVM (or today's centralized block production) would capture more value.

It is not perfect, but given our current situation, this shortcut should be close enough to optimal. The vast majority of MEV will still use disjoint access lists, as conflict examples like the one above are very rare.

6. Timestamp - Homomorphic

You can even attempt to hide the leak of transaction existence by allowing validators to perform "virtual" transactions, so the mempool is always filled. Validators also need a SNARK to prove they are the validators allowed to create these virtual transactions. When "real" transactions peak, validators will broadcast fewer virtual transactions. When real transactions decline, validators will issue more virtual transactions.

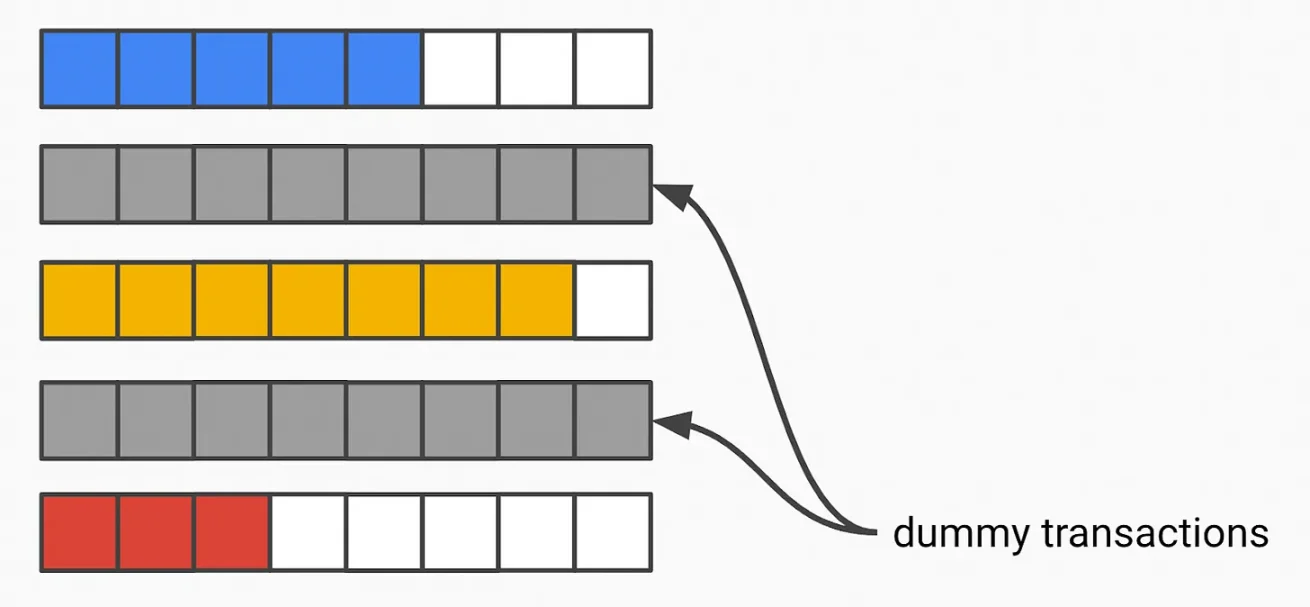
Assuming everything uses FHE encryption, you will be able to detect the "virtual flag" added to the corresponding transactions. You can ignore these transactions when packing the actual block.

State Differences - FHE EVM

Background overview: One advantage of ZK Rollups is that they do not need to publish complete transaction data on-chain. It is sufficient for them to publish the "state differences" between state updates. In contrast, Optimistic Rollups must publish complete data on-chain to arbitrate fraud proofs. This lower data requirement saves costs for ZK Rollups, as they consume fewer resources in the data availability layer.

Bringing this into our discussion ------ ideally, you do not want to lose this benefit in the case of encrypted mempools. You want to achieve encrypted mempools while still retaining the ability for ZK Rollups to only publish state differences. The answer lies here ------ FHE zkEVM. Sounds cool, but you may have to wait a long time.

One downside is that publishing state differences alone may reduce the responsiveness of Rollup full nodes. For example, in a pure fork-choice rule Rollup, full nodes can complete their view of the Rollup immediately when the data availability layer is complete and ensures validity. If you only publish state differences (rather than complete transaction data), even full nodes need to submit ZK proofs to confirm their view of the Rollup. As it stands ------ these proofs take time to generate, but scalable data availability layers are expected to become very cheap soon.

Conclusion

Encrypted mempools are a fascinating and promising design space, but there are still some practical challenges. For example, you may just be shifting certain issues to other places in the stack. Wallets can censor you at the source to prevent transaction encryption/routing, they can submit payloads to run before/after your transaction (or sell rights), etc. One possible answer is for users to create transactions locally without relying on service providers.

The key point is that there is no silver bullet here, but if designed properly, they could be an important part of the solution, improving the current situation through different functionalities and trust assumptions.