Learn about Opyn's new product Squeeth: pioneering a new track in derivatives

As the title suggests, this article will not introduce the traditional options products offered by Opyn, but will instead focus on analyzing a new category of derivatives developed by them: Squeeth. This product is built on the concept of "Power Perpetual Contracts" proposed by the renowned investment research institution Paradigm in their paper from August 2021. In the following text, we will analyze using concise language and common cases, so readers without a financial background need not be discouraged.

When it comes to derivatives, people often think of high-leverage speculative tools used by traders to bet on price fluctuations. However, in reality, derivatives were originally designed to help users transfer risk more efficiently (similar to buying insurance). Therefore, in this article, we will not simply view Squeeth as a newly emerged high-leverage speculative tool, but will return to its essential properties to see what roles Squeeth can play when users face risks they do not want to bear.

The most common application scenario for crypto users is probably liquidity mining. The booming crypto world offers users yields far exceeding those in traditional industries. However, when users participate in mining activities, they are often forced to hold some tokens that they do not understand and do not want to hold. In the two cases below, we will intuitively explain how Squeeth helps investors transfer the "impermanent loss" risk of dual-token mining pools.

However, since the dual-token pool model is more complex, let’s start with a simpler single-token pool case.

How to Risk-Free Enjoy the Returns of a Single-Token Mining?

You suddenly discover a project called JQK that is holding a single-token staking rebate event with an annualized yield of up to 500%. You do not know and completely do not want to know what this project called JQK is doing; you just want to enjoy the 500% yield for free. What should you do? (In an ideal environment, without considering contract vulnerabilities, derivative price decoupling, and other risks)

You take out $1,000 as your principal to participate in this investment. According to the event requirements, you first need to exchange this $1,000 for JQK and stake it in the project contract. Once you exchange the $1,000 for JQK, which you completely do not understand, the subsequent market value of this $1,000 asset will be directly affected by the price fluctuations of JQK.

If we take the market value of all the assets you hold at this time as the vertical axis and the price of JQK as the horizontal axis, we will get the market value curve of your investment portfolio.

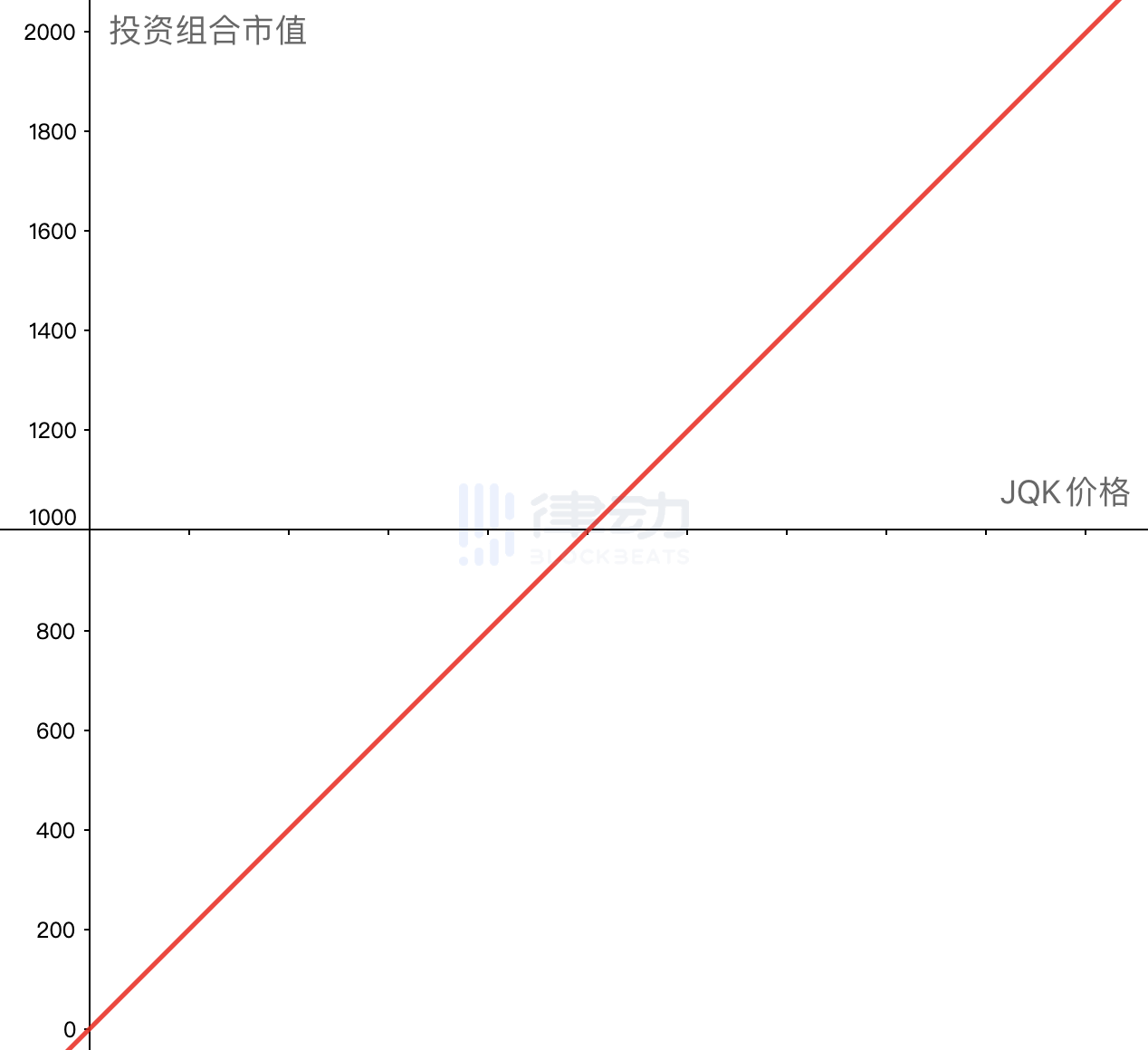Since you just want to enjoy the mining yield of up to 500%, and do not understand or want to bear the risk of holding JQK, you hope to transfer this part of the risk, making the fluctuations of JQK irrelevant to you. In other words, you want your investment portfolio's market value curve to become a horizontal line.

At this point, you can short an equivalent amount of JQK using JQK futures or perpetual contracts. The market value curve of the short position in JQK is as follows:

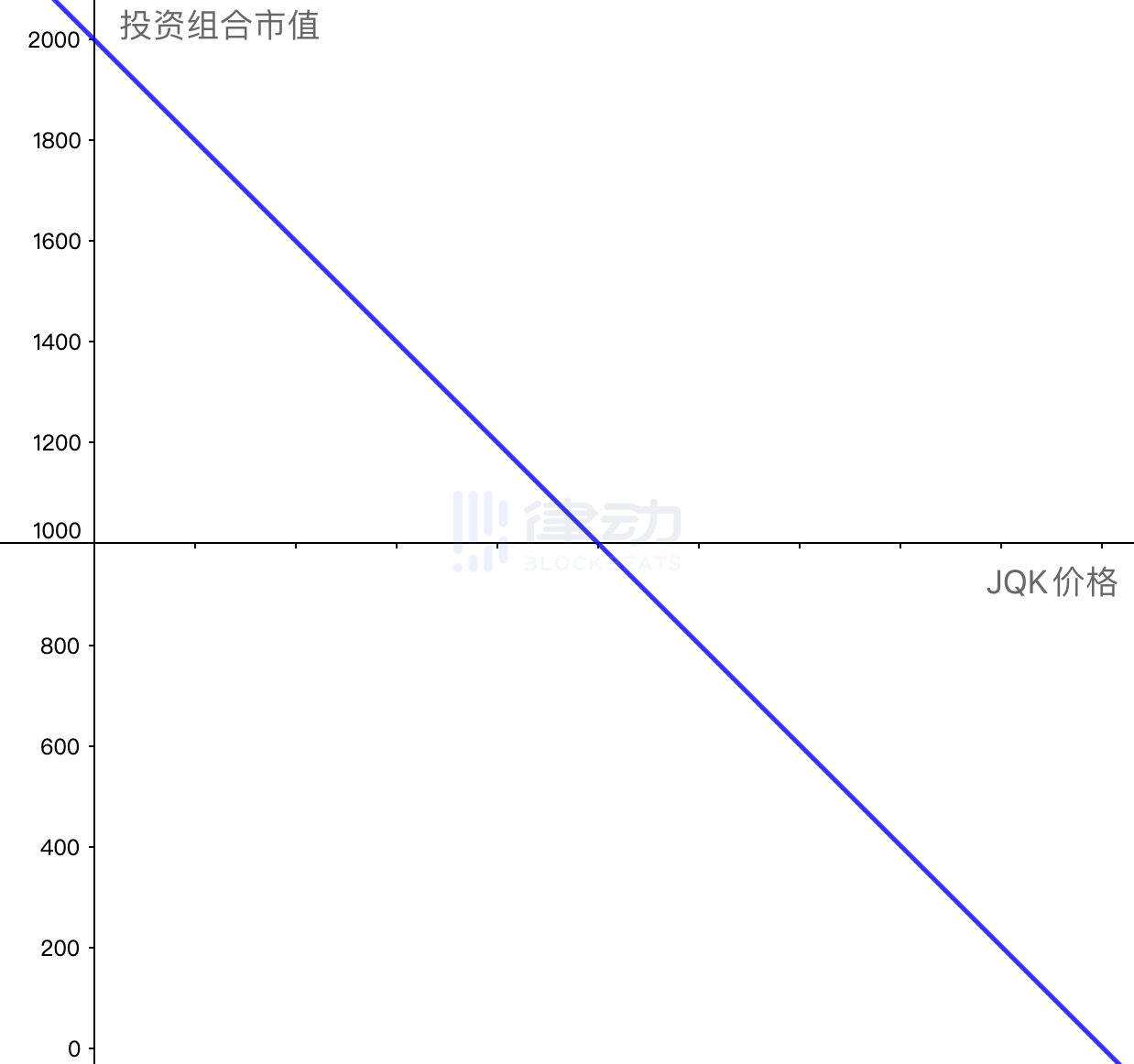It can be seen that the diagonal line in Figure 2 is exactly the reflection of Figure 1. Therefore, if both are added to your investment portfolio simultaneously, the final result of the combination will be the sum of the profits and losses of both at every point.

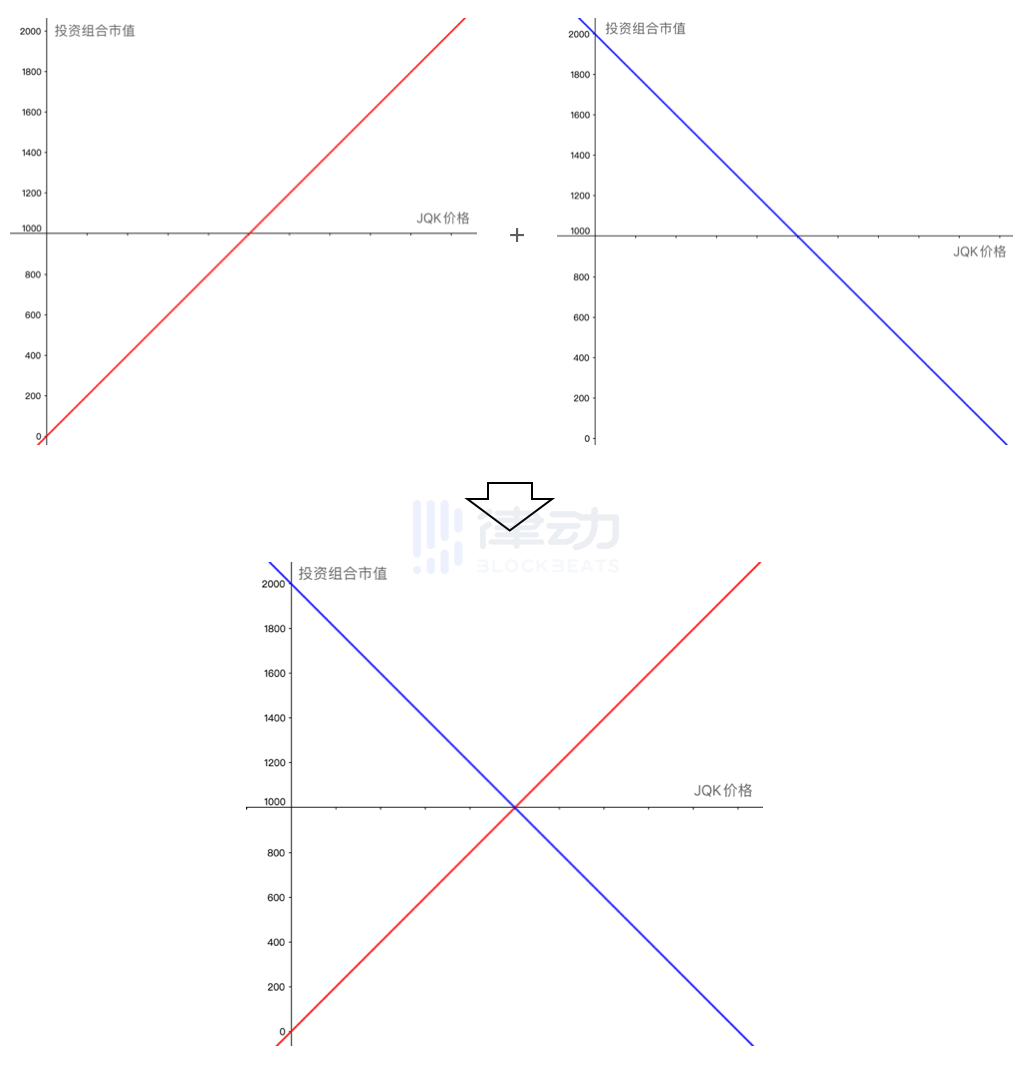Since the profits and losses of both are equal in magnitude but opposite in direction at every point, the result of their addition is a horizontal line. At this point, you can enjoy a risk-free stable yield of 500% without worrying about the price fluctuation risk of JQK.

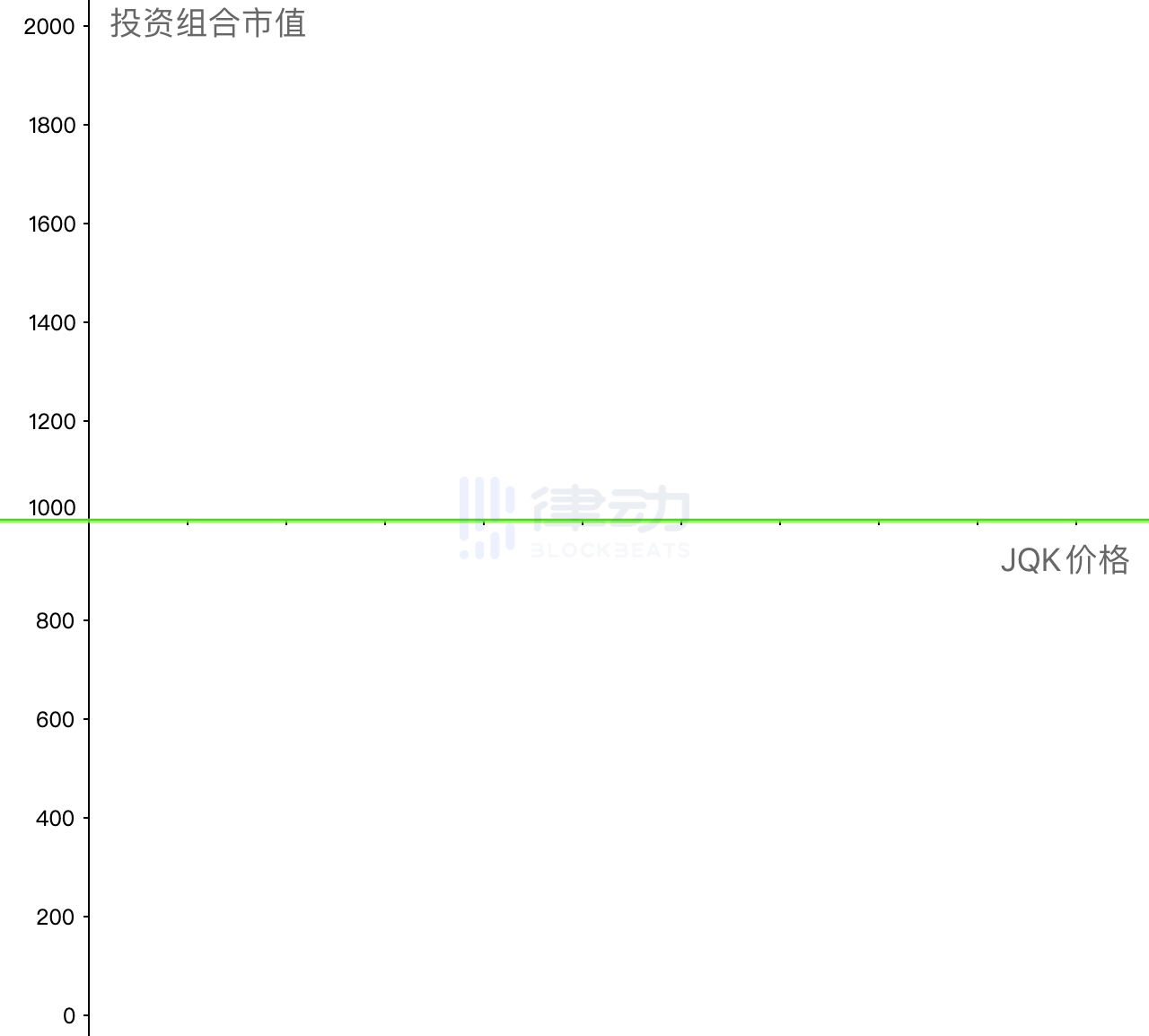
The operation described above is professionally called hedging, and is sometimes referred to as hedging, primarily used to help investors transfer risks they do not want to bear. After understanding the simple risk transfer method for single-token pools, let’s look at the more complex dual-token pool.

How to Risk-Free Enjoy the Returns of a Dual-Token Mining Pool?

Suppose you discover another project called QKA, which is holding a dual-token liquidity mining event on an AMM trading platform with an annualized yield of up to 500%. You do not know and completely do not want to know what this project called QKA is doing; you just want to enjoy the 500% yield for free. What should you do? (In an ideal environment, without considering contract vulnerabilities, derivative price decoupling, and other risks)

From the previous case, we have learned that to mine risk-free, we need to adjust the market value curve of the investment portfolio to a horizontal line. Therefore, we first need to know what the market value curve of the dual-token LP position looks like.

Compared to the single-token pool image, the dual-token pool image is clearly much more complex. First, the image of the dual-token pool has changed from a straight line to a curve. Therefore, the first problem we need to solve is to straighten this bent curve.

At this point, we need to find a new derivative to help us achieve this goal. For this new derivative, its own market value curve must also be curved, as only then can it be used for reverse hedging. Secondly, the direction of this curve's curvature must be opposite to that of the dual-token pool.

At this moment, the protagonist of this article, Squeeth, can finally make its appearance. We will not explain what Squeeth is for now; let’s first take a look at its market value curve.

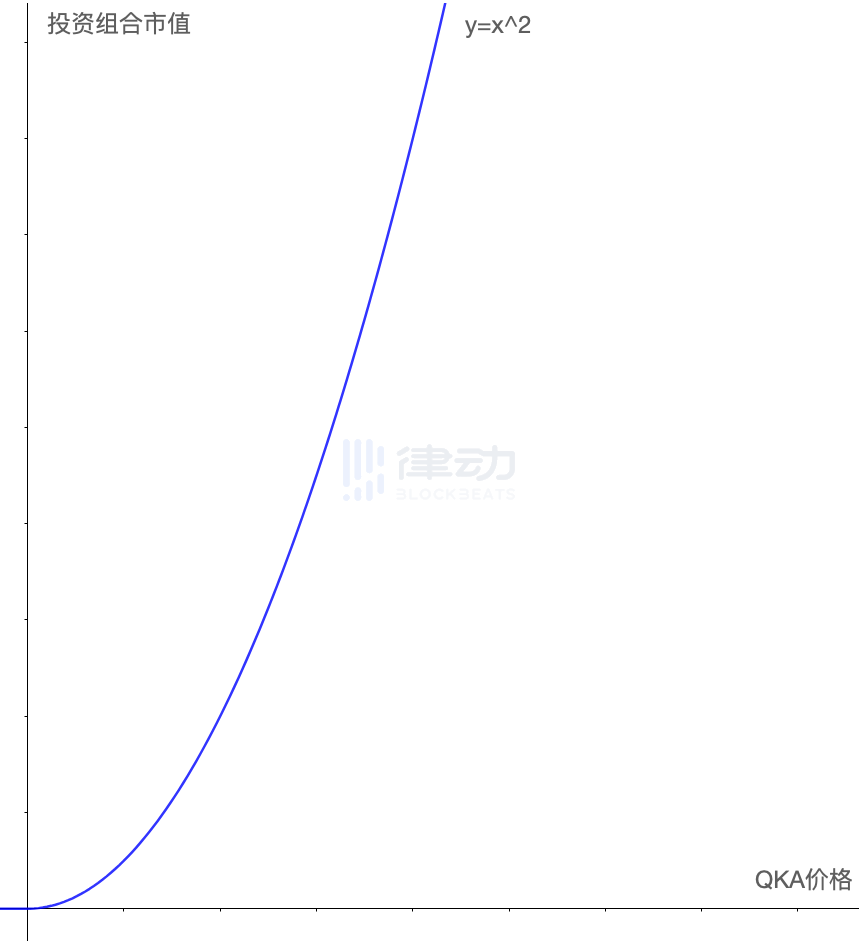It can be seen that the shape of Squeeth's curve perfectly meets the conditions we initially proposed. Not only is it also a curved line, but its curvature direction is opposite to that of the curve that needs to be hedged. Therefore, as long as we adjust the mixing ratio of the two, we hope to fit them into a straight line.

After some trials, we mixed the two curves in a ratio of 1:100, and the final fitting result is the green curve shown in the figure below. It can be seen that, except at extreme values (when the price of QKA is very small or very large), the green curve is already very close to a straight line.

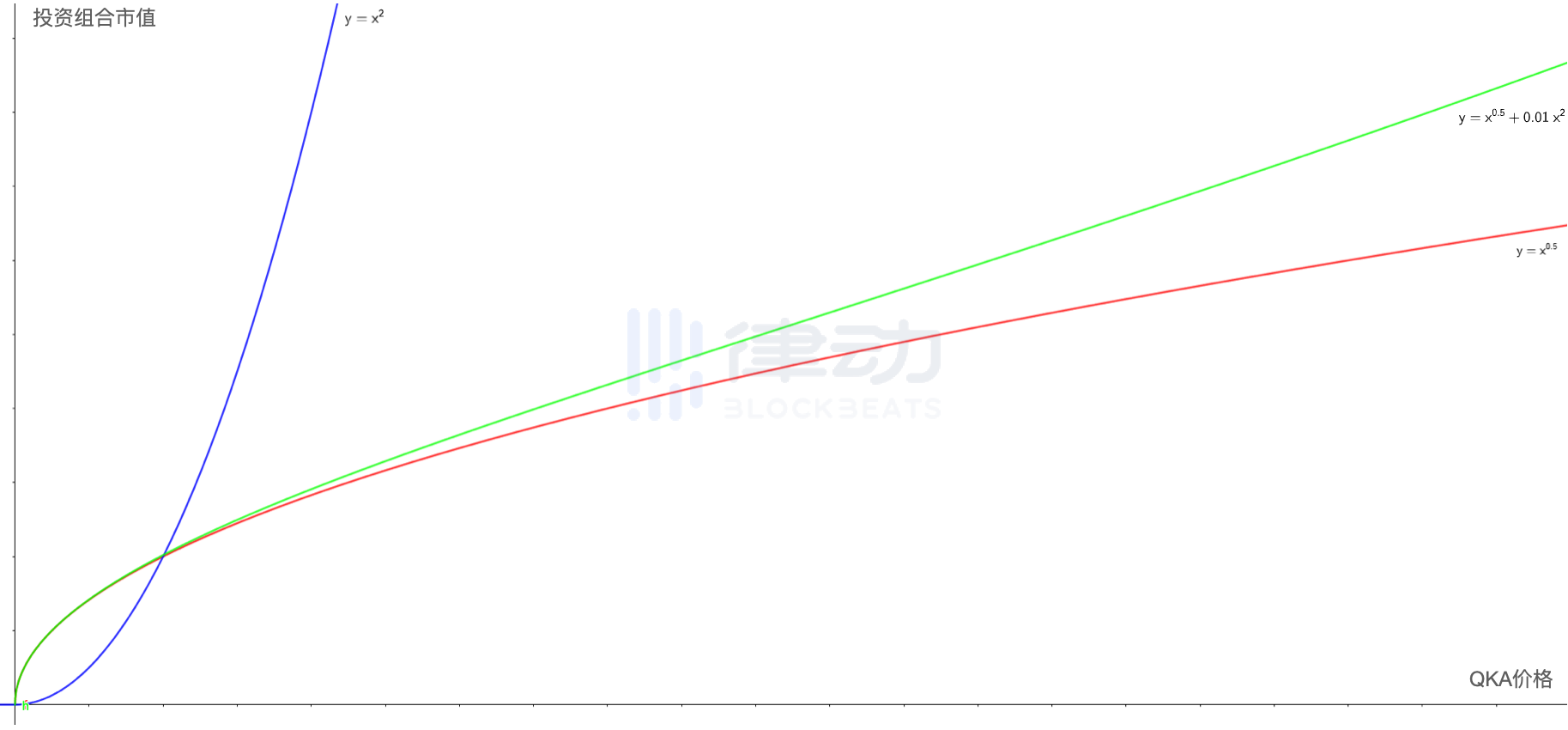The subsequent work is quite simple. For this green line that still has a certain slope, as long as we use perpetual contracts or futures to make slight adjustments to its slope in the same way as in Case 1, we can achieve our initial goal. By mixing the two functions in a ratio of about 3:1, we can obtain the new function graph represented by the yellow line in the figure, which is already very close to a horizontal line.

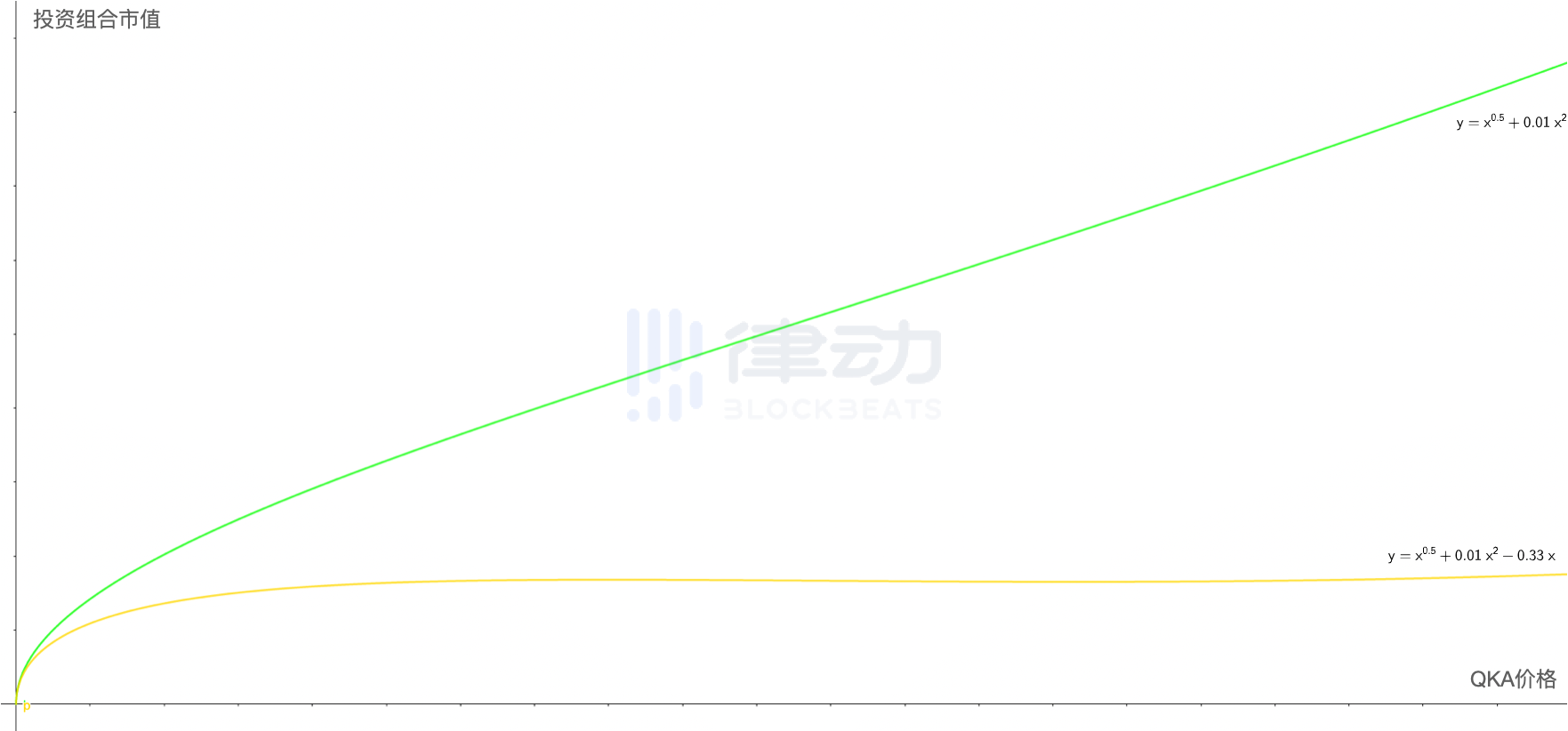At this point, as long as the price of QKA does not go to zero, you can happily enjoy the 500% risk-free yield from this dual-token pool. (Note: All the above cases are not rigorous mathematical proofs, but are intended to intuitively demonstrate the main logic behind the entire process.)

The second case mentioned earlier is likely to be the most probable application scenario for Squeeth in the future. Here, we will not analyze the basic principles behind the power perpetual contracts in detail; instead, we will briefly summarize their characteristics. Readers who wish to learn more can refer to our earlier analysis article: “How to Understand Paradigm's Power Perpetual Contracts.”

1. Power perpetual contracts are essentially not options; their basic product logic is more like perpetual contracts;

2. The main difference between power perpetual contracts and perpetual contracts is that their target function changes from y=x to y=x^n;

3. Squeeth is a special form of power perpetual contracts when n=2;

4. Since power perpetual contracts also exhibit a curve on the function graph like options, they have usage scenarios more similar to options rather than futures, hence they are also referred to as quasi-option products (like options but not options);

However, since the publication of the paper, power perpetual contracts have remained a novel concept that has only existed in academic papers. To turn it into a truly usable product, a lot of complex design and development work is still needed.

Productization of Power Perpetual Contracts: Squeeth

Since the publication of the paper, the Opyn team has been conducting more detailed engineering design for its specific product plan over the past six months, during which they have naturally faced many tricky problems.

Compared to traditional perpetual contract products, Squeeth's target function y=x^2 has a larger price fluctuation range, making it difficult to directly apply the traditional perpetual contract margin trading model to Squeeth. However, if margin trading is not adopted, the funding fees that maintain the price anchoring of perpetual contracts lose their means of payment.

If these issues cannot be effectively resolved, the product concept of Squeeth may only remain at the theoretical stage. Therefore, the Opyn team has boldly innovated its trading model.

1. Improved Margin Trading Mechanism

Traditional perpetual contract trading platforms generally rely on a margin trading system. This mechanism provides investors with leverage trading capabilities but also makes it difficult for investors' trading positions to exist independently of the margin platform. In other words, the positions held by investors on the platform are hard to tokenize. This confines these positions to a closed space, making it difficult to enjoy the excessive liquidity support of the crypto world.

To exempt Squeeth holders from paying margin, Opyn directly locks the leverage multiple of the product's long position to one. By eliminating liquidation risk, they can directly tokenize the long position of the Squeeth product. The tokenized version of Squeeth is called oSQTH, which can be freely traded outside the Opyn platform. Users needing to hedge risks with Squeeth can directly purchase it through Uniswap.

However, since the losses of short position holders have no lower limit, they cannot be exempted from margin like the long position. Before minting oSQTH, the short position must first pledge a certain amount of ETH to the platform to ensure that liquidation can occur in extreme situations.

At this point, you may have noticed that the Squeeth product has evolved from an initial margin trading perpetual contract-like product into an asset minting and issuance platform.

2. Revolutionizing Funding Fee Payment Methods

We know that the foundation for maintaining perpetual contract-like products and anchoring the target function price is the funding fee system. However, after changing to an asset minting and issuance platform, this fundamental basis no longer exists. To solve this problem, Opyn invented a new anchoring mechanism, known as in-kind funding.

The idea of in-kind funding is quite simple: since there is no money, why not use the held oSQTH tokens to make the payment? Under this assumption, the oSQTH assets held by the holder decrease after paying the short position, while the short position's obligation to redeem ETH decreases as well when they receive oSQTH.

However, since both parties' assets and liabilities decrease proportionally, could we simply avoid frequent payments of oSQTH and directly adjust the relative redemption price of oSQTH to ETH?

Let’s take a practical example. The short position initially pledged one ETH to issue 100 units of oSQTH. A month later, the calculated funding fee rate based on the market transaction price should be 10%. At this point, the system no longer deducts oSQTH from the long position's account; instead, it directly adjusts the amount of oSQTH that the short position needs to return to the system when redeeming 1 ETH from 100 to 90 units of oSQTH.

In this way, the short position's liability directly decreases by 10%, equivalent to earning a 10% profit. This parameter that adjusts the short position's liability repayment ratio is called the normalization factor.

This model is quite similar to Compound's interest calculation method, where the number of cTokens held by depositors does not increase with the accumulation of interest. However, the system continuously adjusts the exchange rate between cTokens and the deposited assets. When you withdraw your assets, the same number of cTokens can redeem more original assets than when they were deposited, and the excess part is the interest for the depositors.

The biggest advantage of this design is that the payment of funding fees no longer requires frequent on-chain transactions. However, since all the impacts of funding fees are directly reflected in the price of the oSQTH token, in the long run, the price of oSQTH will inevitably deviate from the ETH^2 it tracks.

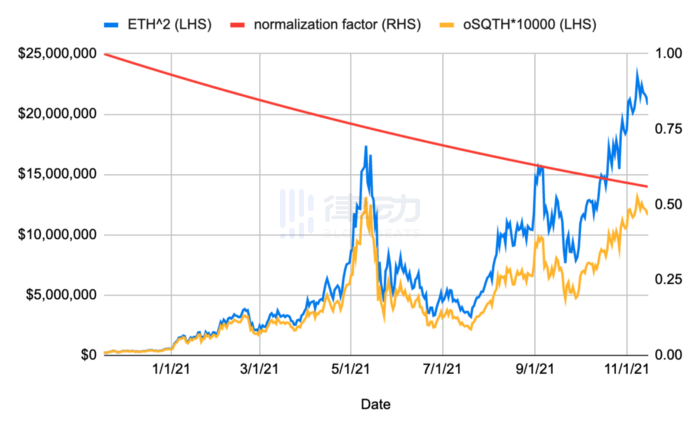As shown in the figure above, the price of the yellow oSQTH will gradually fall below the target price of ETH^2, and this difference represents the funding costs accumulated by the long position. The degree of deviation will gradually widen as the price of the normalization factor represented by the red line decreases.

The Significance and Shortcomings of Squeeth

1. Main Significance

Uniswap and Curve are currently the two most important DEX projects in the Ethereum ecosystem. Among them, the fully functional Uniswap has a richer application scenario compared to Curve, which mainly targets stablecoins. However, from the total locked funds of both, we see a completely opposite phenomenon. For a long time, the total locked funds in Curve have far exceeded those in Uniswap.

One significant factor that cannot be ignored is that Curve's liquidity pools, whether stablecoins or non-stablecoins, come with an impermanent loss management mechanism. This allows Curve's LPs to treat it as a passive management fund purchase without needing to constantly monitor the impermanent loss issue.

In contrast, LPs on Uniswap, whether in V2 or V3 versions, cannot ignore the issue of impermanent loss. If LPs neglect it, the funds they deposit often end up being worth less after a period of time.

Although there are currently many solutions to reduce impermanent loss for Uniswap LPs, these projects often rely on active rebalancing mechanisms. Until the emergence of Squeeth, there was finally a new solution for passive management of impermanent loss for Uniswap LPs. In the future, perhaps projects can build risk-free Uniswap liquidity pools based on Squeeth and conventional perpetual contracts and other derivatives, allowing Uniswap LPs to also earn passive and risk-free market-making fee income like those in Curve.

Additionally, the Squeeth product has innovatively addressed the most severe flaw of traditional options products, which is the liquidity fragmentation caused by strike prices and expiration dates. If it proves that Squeeth can indeed replace traditional options in most application scenarios, its significance for the development of the financial industry will be immeasurable. Of course, this conclusion still needs to be tested in the real market.

2. Shortcomings and Limitations

Strictly speaking, Squeeth cannot completely hedge all shapes of curves. Even in the dual-token pool case mentioned above, Squeeth cannot achieve perfect hedging; it can only roughly straighten the curve. Theoretically, to perfectly hedge the dual-token position risk of an AMM liquidity pool, a power perpetual contract product with n=0.5 would need to be developed, but this demand may have to wait for Opyn's next phase of product development plans.

Moreover, for ordinary users, the usage of Squeeth still seems overly complex. Therefore, it is hoped that Opyn will not only launch a token called oSQTH in the future but will also design some simple and usable comprehensive solutions for specific scenarios, allowing users to transfer risks with one click without needing to understand the basic logic of derivatives. Perhaps such services would be the killer application that could truly break the deadlock in the derivatives field.

Finally, Opyn's Squeeth product is expected to go live on the Ethereum mainnet on January 10 and will launch on Ethereum Layer 2 platforms by the end of the first quarter, at which point users can go and experience it.

Bonus at the End ------ Option Greeks

In the main text, to explain the basic principles of hedging more intuitively, we used too many descriptive terms like slope and curvature in the examples. However, in actual operations, we still need quantitative reference indicators to calculate the number of derivatives needed to purchase for risk transfer. These quantitative reference indicators are conventionally represented by Greek letters. Below, we will introduce the three most common Greeks in layman's terms. (Of course, the following statements are not rigorous; they are only intended to give beginners an intuitive understanding.)

1. Delta (Slope Degree)

Delta is used to describe the slope degree of the investment portfolio price curve. The more severe the slope, the larger the Delta value; an upward slope is positive, while a downward slope is negative. Therefore, if you know that the Delta value of your investment portfolio is 1, then the Delta value of the derivatives you need for hedging should be -1.

2. Gamma (Curvature Degree)

Gamma is mainly used to describe whether your investment portfolio price curve is bent. When hedging, it is necessary to make the hedged Gamma value as close to zero as possible (which is to straighten the curve as in Case 2).

3. Vega (Implied Volatility)

The price of a health insurance policy with completely identical conditions sold to an 80-year-old is bound to be much higher than that sold to a 20-year-old. The underlying logic is that the probability of health issues arising for an 80-year-old is certainly much higher than that for a 20-year-old.

Therefore, if you want to accurately assess the probability of health risks occurring in different age groups, in addition to collecting a large amount of medical data for statistical analysis, a more clever approach is to directly observe the premium prices set for the same health insurance policy across different demographics. The higher the premium, the higher the implied probability of health issues.

This risk level reflected in the prices of risk management products is known as the implied volatility of the product.

If we replace the health insurance policy in the example above with an options product, we can indirectly judge the probability of price fluctuations in the future by directly observing the market prices of the same options product. As long as this is an open and freely competitive efficient market, the price discovery function of the market will automatically reflect everyone's consensus on future price volatility.

Vega reflects the sensitivity of option prices to implied volatility. Therefore, we can easily derive everyone's expectations for future volatility using specific algorithms.

The Squeeth product, like options, can also indirectly derive the implied volatility of future prices through its price. Moreover, due to the uniformity of liquidity, it will inevitably make the price game more sufficient. Therefore, compared to traditional options products, the implied volatility obtained through Squeeth may be more representative.