3.1 Secret Engine

認識到每個零知識證明系統都由兩部分組成：一是算法，二是多項式承諾方案。將程序轉化為零知識證明(ZKP)的初始階段涉及到算法。這個過程通過在這些多項式之間建立特定的條件來闡明它們之間的關係。

我們的零知識證明系統是基於標準 PlonK 配方實現的，具有高度定制的 gates，主要包括：

• 小工具：支持遊戲電路開發中使用的各種小工具，包括基本算術電路、哈希、ECC、zkshuffle、zkmatchmaking等。我們建議訪問我們的 GitHub 存儲庫以獲取有關這些小工具的更多信息。

• 鏈上驗證器：為證明者和驗證者優化了PLONK/ZKVM，同時支持所有EVM鏈的通用可靠性驗證器。

• 應用程序特定的 Plonk：使用應用程序特定的 Plonk 作為基本方案ZK證明，用我們的SDK提供的各種小工具來編寫特定的遊戲電路。同時我們還提供不同虛擬機（EVM/WASM/…）上的驗證合約，可以運行在不同的區塊鏈系統中，實現鏈下證明和鏈上驗證。

接下來，我們將介紹兩個重要的組件，由Secret Engine孵化的zkshuffle和zkmatchmaking。

3.1.1 ZK shuffle SDK

3.1.1.1 介紹

撲克遊戲是一種備受歡迎的紙牌遊戲。在現實生活中，遊戲各方可以相互監督，以確保遊戲的公平性。隨著計算機網絡的快速發展，通過網絡連接的玩家也有了參與撲克遊戲的機會，儘管如此，網絡環境下如何確保遊戲的順利進行和公平性卻是一個不小的挑戰，這也是心理撲克協議所要解決的問題。

心理撲克是一種基於密碼學原理構造的撲克遊戲，自1979年Shamir、Rivest和Adleman提出了第一個心理撲克協議【15】以來，人們就開始研究心理撲克遊戲的可行性。心理撲克與普通撲克玩法類似，主要區別在於心理撲克是在沒有物理卡牌的網絡環境中進行，且所有玩家默認是不誠實的，即存在作弊行為。第一個心理撲克協議是一個兩方的撲克協議，該協議已經被證明存在安全漏洞。根據文獻【16】,一場公平的心理撲克必須滿足以下屬性：

1. 唯一性：在傳統撲克遊戲中，通過明示卡牌以驗證沒有重複的卡牌。心理撲克協議應保證同樣的特性。

2. 隨機分布：在傳統撲克遊戲中，一名玩家進行洗牌，其他玩家可以實時觀察，這意味著洗牌的玩家無法控制最終的洗牌結果。

3. 保密性：任何時候，如果牌堆是面朝下的，就不應該透露關於牌堆中任何卡牌的信息。此外，當玩家抽取一張卡牌時，其他玩家是不能夠獲取關於該牌的任何信息。

4. 沒有可信第三方：依賴可信第三方是不行的，因為任何人都可以被收買，沒有絕對可信的第三方。

1987年，Crépeau提出第一個安全的心理撲克協議【17】。此後，心理撲克協議方案開始湧現，但很大部分心理撲克協議的研究是基於TTP的，因為學術界廣泛認為採用TTP是解決心理撲克協議公平性的有效辦法。然而撲克作為一種娛樂、休閒遊戲，很多場景並不存在第三方，也很難確保第三方可信，特別是在涉及區塊鏈技術的情況下，通常不存在一個可信第三方，因此如何在無PPT的條件下實現公平的心理撲克協議具有重要的意義。Barnett-Smart協議【18】於2003年提出，它提供了兩種解決方案，分別基於ElGamal和Pailler加密系統，但Pailler加密方案存在一個安全上限，即假設合謀人數不超過(N-1)/2。隨後，Castellà-Roca協議【19】提出，其採用了不同的加密方案，shuffle過程也比Barnett-Smart協議要快。

心理撲克協議開銷主要集中在shuffle部分，但在今天零知識證明算法取得了快速的發展，如geometry【20】【21】指出，shuffle過程已經不再是一個瓶頸，並且geometry認為Barnett-Smart協議將完整的紙牌遊戲協議需要劃分成多個安全子協議：生成卡牌、masking、re-masking、shuffle等等，這些步驟可以輕鬆實現即插即用，其安全性假設也基於Decisional Diffie-Hellman。因此，我們的mental poker協議主要借鑒Barnett-Smart協議，但同時也考慮到在對一套撲克牌進行zkShuffle涉及到大量椭圆曲线運算，其電路規模必然相當龐大。為了解決這個問題，我們重新設計一種zkshuffle友好的TurboPlonk【22】算法，顯著降低了電路門的規模。

3.1.1.2 基本概念

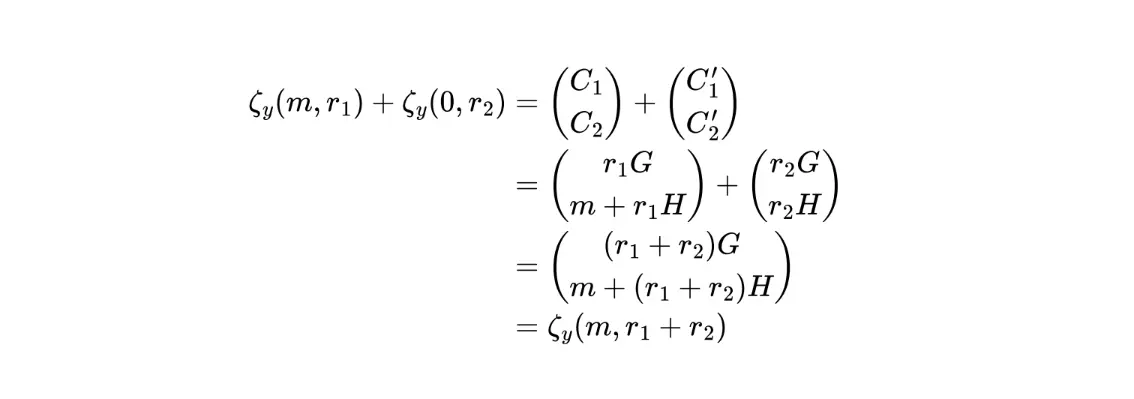
注：n-out-of-n threshold EIGamal encryption【23】

3.1.1.3 心理撲克協議

Mental poker 協議不是一個協議，而是包括了一組子協議，每個子協議負責一個行為。

• Key Generation:

• 為每一個玩家生成公私鑰對
• 聚合所有玩家的公鑰以生成一個公鑰

• Masking:

• Masking函數是在聚合公鑰下的一種ElGamal加密函數

• Shuffle and Re-masking:

• 執行洗牌操作以達到隨機化卡牌的目的
• 對shuffle之後的卡牌再次進行mask

• Unmask:

• 解碼卡牌以獲取真實的卡牌信息

Key Generation protocol

Masking protocol

Re-Masking protocol

Shuffle argument

Unmask protocol

3.1.1.4 洗牌友好 PLONK 算法

Shuffle 協議主要包括兩部分：1)對卡牌進行置換；2)對卡牌進行re-masking；其中 re-masking 操作涉及椭圆曲线運算，具體包括 1 個 Constant-base scalar multiplication、1 個 Non-constant-base scalar multiplication 和 2 個 curve addition，如果使用非優化TurboPlonk定制門(customized gates)來編寫算術電路，對一張卡牌的re-masking的電路門數為596+1622+2=2220，那麼對一套完整的牌組(52張)來說，電路門數將高達115440，這還不包括置換相關的電路。因此，如果採用非優化的TurboPlonk來編寫算術電路，其shuffle時間將會非常漫長。為了解決這個問題，我們重新改造了TurboPlonk使其對shuffle運算友好，經過驗證，對一個re-masking操作只需要 85 gates。

注：bowe hopwood【24】

3.1.1.5 鏈上驗證

此外，在我們實踐中，我們還遇到鏈上驗證gas費高的問題，這裡將主要和大家分享我們優化心得。

Verify reveal 解密一張卡牌，需要其它玩家提供相應的開牌信息，同時提供一個證明，用於驗證開牌的正確性。現有Geometry的現實【25】基於chaum pedersen協議構造了一個開牌證明，我們知道chaum pedersen需要點乘運算，點乘操作是非常昂貴，主要因為目前以太坊不支持Baby Jubjub這條曲線的預編譯合約，根據測試結果，基於Geometry實現下，驗證開牌證明的gas費高達7629888，這顯然是不可接受的。

考慮到 Baby Jubjub 是 BN254 的內嵌曲線，我們可以使用Snark進行開牌證明，根據gas的分析【26】,使用Groth16進行開牌證明的鏈上驗證開銷僅為約200k，這幾乎比原生驗證方式下降了30倍。相比於原生的驗證方式，這似乎是一個非常不錯的選擇，開牌circuit如下：

未來，我們進行proof 聚合來更大程度的節省gas。

Verify shuffle 在德州撲克遊戲中，我們需要將洗牌後的結果存儲在鏈上，這不僅作為當前的shuffle結果，也用於後續shuffle circuit的公開輸入。然而，一副撲克牌有52張，共計208個uint256類型數據，其鏈上存儲成本昂貴。

我們的方案是只在鏈上存儲部分撲克牌數據，具體來說，我們只需要存儲2n+5張卡牌，其中n為玩家數量。考慮到我們的遊戲最大同時支持6個玩家，因此最多只會用到17張牌。這意味著我們最終只需要在鏈上存儲17張卡牌，節省了2/3存儲開銷。

儘管我們最終只需要在鏈上存儲17張牌，但前文提到鏈上存儲的另一個目的是，這些牌也將作為後續shuffle circuit的公開輸入。因此如果只存儲17張牌，就無法驗證shuffle的正確性。為了解決這個問題，我們Shuffle電路會額外輸出一個完整撲克牌的哈希值，存儲在鏈上。在驗證zkShuffle時，會作為電路的public input，從而保證了shuffle的正確性。

3.1.2 ZK matchmaking SDK

Matchmaking是一種旨在通過根據玩家水平進行遊戲匹配的機制，以確保玩家在遊戲中能夠與實力相當的對手展開對戰，從而提供公平且有趣的遊戲體驗。Matchmaking的核心目標可概括為以下兩方面：

• 公平對抗：提供實力相當的玩家對抗，以使雙方獲勝的概率都盡可能傾向於50%。

• 不可預測性：匹配過程不可預測，即最終對戰的選手不可預測。

整體流程

1. 申請成為 Prover 時，需向合約承諾一個種子，這個種子只有 Prover 知曉

2. 玩家發送加入遊戲請求

3. 排序器接收到請求後，根據分級策略進行排序，然後將生成的隊列分別發送給合約和證明者

4. Prover 基於 zkSnark 對不同隊列進行隨機匹配，匹配的結果依賴於 Prover 承諾的種子、輸入的隊列，以及鏈上隨機數(確定的，但不可預測的)，然後將匹配的結果和 proof 發送給合約

5. 合約進行鏈上驗證，如果驗證通過，玩家根據匹配結果進入遊戲

在區塊鏈上，我們可以輕鬆獲取像 block hash 那樣的鏈上隨機數，但它會受到礦工和驗證者的區塊扣留攻擊，導致像 block hash 那樣的鏈上隨機數不是十分安全，以至於 Matchmaking 的不可預測性也會受到挑戰。可驗證隨機函數 VRF 是一種具有驗證性質的隨機數生成器，能夠生成統計上均勻不可預測的隨機輸出，並且其輸出是可驗證的，這為我們鏈上隨機數提供了一種很好的解決方案。讓我們簡單了解下 VRF 的原理吧，其輸入一個seed，輸出一個隨機數。

除了鏈上隨機數，不可預測性也依賴於 Prover 承諾的種子，我們會構建懲罰機制來防止 Prover 隨意洩漏隨機數。

參考文獻 ：

【15】A. Shamir, R. L. Rivest and L. M. Adleman, Mental poker, Technical report LCS/TM-125, Massachusetts Institute of Technology, April 1979.
【16】Crépeau C. A secure poker protocol that minimizes the effect of player coalitions, in: Conference on the Theory and Application of Cryptographic Techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 1985: 73--86.
【17】C. Crepeau, A zero-knowledge poker protocol that achieves confidentiality of the players' strategy or how to achieve an electronic poker face, in: Advances in Cryptology -- Crypto 086, Lecture Notes in Computer Science 263, Springer-Verlag, Berlin (1987), 239--247.
【18】A. Barnett and N. Smart, Mental poker revisited, in: Cryptography and Coding, Lecture Notes in Computational Science 2898, Springer-Verlag, Berlin (2003), 370--383.
【19】J. Castellà-Roca, Contributions to mental poker, Ph.D. Thesis, Autonomous University of Barcelona, Doctoral Programme in Computer Science and Artificial Intelligence, 2005.
【20】N Mohnblatt, A Novakovic and K Gurkan, Mental Poker in the Age of SNARKs - Part 1,
https://geometry.xyz/notebook/mental-poker-in-the-age-of-snarks-part-1
【21】N Mohnblatt, A Novakovic and K Gurkan, Mental Poker in the Age of SNARKs - Part 1,
https://geometry.xyz/notebook/mental-poker-in-the-age-of-snarks-part-2
【22】Gabizon A, Williamson Z J. The turbo-plonk program syntax for specifying snark programs, in: ZKProof Workshop. 2020, 3.
【23】Desmedt Y. Threshold cryptosystems, in: International Workshop on the Theory and Application of Cryptographic Techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 1992: 1--14.
【24】https://github.com/arkworks-rs/crypto-primitives/tree/main/crypto-primitives/src/crh/bowe_hopwood.

【25】https://github.com/geometryxyz/mental-poker/blob/main/barnett-smart-card-protocol/src/discretelogcards/mod.rs#L320.

【26】Todd Norton, Groth16 Verification Gas cost,https://hackmd.io/@nebra-one/ByoMB8Zf