用多因子模型構建強大的加密資產投資組合#大類因子分析:因子正交化篇#
書接上回,關於《用多因子模型構建強大的加密資產投資組合》系列文章中,我們已經發布了四篇::《理論基礎篇》、《數據預處理篇》、《因子有效性檢驗篇》、《大類因子分析:因子合成篇》。
在上一篇中,我們具體解釋了因子共線性(因子之間相關性較高)的问题,在進行大類因子合成前,需要進行因子正交化來消除共線性。
通過因子正交化,重新調整原始因子的方向,使他們相互正交([fᵢ→,fⱼ→]=0,即兩個向量相互垂直),本質是對原始因子在坐標軸上的旋轉。這種旋轉不改變因子之間的線性關係也不改變原本蘊含的信息,並且新因子之間的相關性為零(內積為零等價於相關性為零),因子對於收益的解釋度保持不變。
一、因子正交化的數學推導
從多因子截面回歸角度,建立因子正交化體系。
每個截面上可以獲得全市場token在各個因子上的取值,N代表截面上全市場token數量,K表示因子的數量,fᵏ=[f₁ᵏ,f₂ᵏ,…,f៷ᵏ]′表示全市場token在第k個因子上的取值,並且已對每個因子進行了z-score歸一化處理,即 fˉᵏ=0,∣∣fᵏ∣∣=1。
Fₙ×ₖ=[f¹,f²,…,fᵏ]為截面上K個線性獨立的因子列向量組成的矩陣,假設以上因子線性無關(相關性不為100%或-100%,正交化處理的理論基礎)。

通過對Fₘₙ線性變換,得到一個新的因子正交矩陣F′ₘₙ=[f₁ᵏ,f₂ᵏ,…,fₙᵏ]′ ,新矩陣的列向量相互正交,即任意兩個新因子向量內積為零,∀ᵢ,ⱼ,ᵢ≠ⱼ,[(f~ⁱ)'f~ʲ]=0。
定義一個從 Fₙ×ₖ旋轉到F~ₙ×ₖ的過渡矩陣 Sₖ×ₖ

1.1 過度矩陣Sₖ×ₖ
以下開始求解過渡矩陣Sₖₖ,首先計算Fₙₖ的協方差矩陣∑ₖₖ,則 Fₙₖ 的重疊矩陣Mₖₖ=(N−1)∑ₖₖ,即
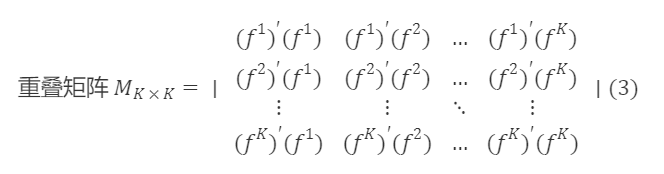
旋轉後的F~ₙ×ₖ是正交矩陣,根據正交矩陣的性質 AAᐪ=I,則有

所以,
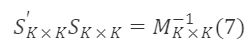
滿足該條件的 Sₖₖ 即為一個符合條件的過渡矩陣。上面公式的通解為:
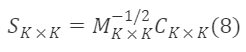
其中,Cₖ×ₖ 為任意正交矩陣
1.2對稱矩陣Mₖ×ₖ⁻¹/²
下面開始求解 M∗ₖ×ₖ⁻¹/²,因為 M∗ₖ×ₖ 是對稱矩陣,因此一定存在一個正定矩陣 Uₖ×ₖ 滿足:
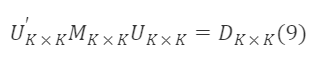
其中,

U∗K×K,D∗K×K 分別為 M∗K×K 的特徵向量矩陣和特徵根對角矩陣,並且 U∗K×K′=Uₖ×ₖ⁻¹,∀ₖ,λₖ>0。 由公式(13)可得
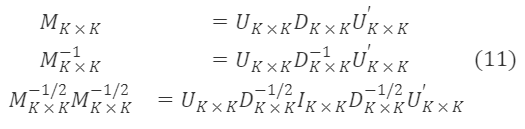
由於 M∗ₖ×ₖ⁻¹/² 是對稱矩陣,且 U∗ₖ×ₖU∗ₖ×ₖ′=I∗ₖ×ₖ,可基於上式得到 M∗ₖ×ₖ⁻¹/² 的一個特解為:

其中

將 M∗ₖ×ₖ⁻¹/² 的解帶入公式(6)可求的過渡矩陣:

其中,Cₖ×ₖ 為任意正交矩陣。
根據公式(12),任何一種因子正交都可以轉化為選擇不同的正交矩陣 Cₖ×ₖ 對原始因子進行旋轉。
1.3消除共線性主要用到3種正交方法
1.3.1 施密特正交
故,S∗K×K 為上三角矩陣,C∗K×K=U∗K×KD∗K×ₖK⁻¹/²U∗K×K′S∗K×K
1.3.2 規範正交
故,Sₖ×ₖ=Uₖ×ₖDₖ×ₖ⁻¹/² ,Cₖ×ₖ=Uₖ×ₖ
1.3.3 對稱正交
故,Sₖ×ₖ=Uₖ×ₖDₖ×ₖ⁻¹/²U′ₖ×ₖ,Cₖ×ₖ=Iₖ×ₖ
二、三種正交方法的具體實現
1.施密特正交
有一組線性無關的因子列向量 f¹,f²,…,fᵏ,可以逐步的構造出一組正交的向量組 f~¹,f~²,…,f~ᵏ,正交後的向量為:

並對 f~¹,f~²,…,f~ᵏ 進行單位化後:
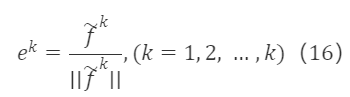
經過以上處理,得到一組標準正交基。由於 e¹,e²,…,eᵏ 與 f¹,f²,…,fᵏ 等價,二者可以相互線性表示,即 eᵏ是 f¹,f²,…,fᵏ 的線性組合,有 eᵏ=βᵏ₁f¹+βᵏ₂f²+…+βᵏₖfᵏ,因此對應於原矩陣 F∗K×K的過渡矩陣S∗K×K 為一個上三角矩陣,形如:
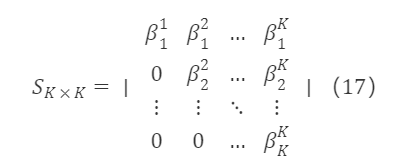
其中
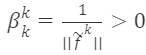
基於公式(17),施密特正交選取的任意正交矩陣為:

施密特正交是一種順序正交方法,因此需要確定因子正交的順序,常見的正交順序有固定順序(不同截面上取同樣的正交次序),以及動態順序(在每個截面上根據一定規則確定其正交次序)。施密特正交法的優點是按同樣順序正交的因子有顯式的對應關係,但是正交順序沒有統一的選擇標準,正交後的表現可能受到正交順序標準和窗口期參數的影響。
# 施密特正交化
from sympy.matrices import Matrix, GramSchmidt
Schmidt = GramSchmidt(f.apply(lambda x: Matrix(x),axis=0),orthonormal=True)
f_Schmidt = pd.DataFrame(index=f.index,columns=f.columns)
for i in range(3):
f_Schmidt.iloc[:,i]=np.array(Schmidt[i])
res = f_Schmidt.astype(float)
2.規範正交
選取正交矩陣 Cₖ×ₖ=Uₖ×ₖ,則過渡矩陣為:

其中 U*K×K為特徵向量矩陣,用於對因子旋轉,D∗K×K⁻¹/² 為對角矩陣,用於對旋轉後因子的縮放。此處的旋轉與不做降維的PCA一致。
# 規範正交
def Canonical(self):
overlapping_matrix = (time_tag_data.shape[1] - 1) * np.cov(time_tag_data.astype(float))
# 獲取特徵值和特徵向量
eigenvalue, eigenvector = np.linalg.eig(overlapping_matrix)
# 轉換為np中的矩陣
eigenvector = np.mat(eigenvector)
transition_matrix = np.dot(eigenvector, np.mat(np.diag(eigenvalue ** (-0.5))))
orthogonalization = np.dot(time_tag_data.T.values, transition_matrix)
orthogonalization_df = pd.DataFrame(orthogonalization.T,index = pd.MultiIndex.from_product([time_tag_data.index, [time_tag]]),columns=time_tag_data.columns)
self.factor_orthogonalization_data = self.factor_orthogonalization_data.append(orthogonalization_df)
3.對稱正交
施密特正交由於在過去若干個截面上都取同樣的因子正交順序,因此正交後的因子和原始因子有顯式的對應關係,而規範正交在每個截面上選取的主成分方向可能不一致,導致正交前後的因子沒有穩定的對應關係。由此可見,正交後組合的效果,很大一部分取決於正交前後因子是否有穩定的對應關係。
對稱正交儘可能的減少對原始因子矩陣的修改而得到一組正交基。這樣能夠最大程度地保持正交後因子和原因子的相似性。並且避免像施密特正交法中偏向正交順序中靠前的因子。
選取正交矩陣 Cₖ×ₖ=Iₖ×ₖ,則過渡矩陣為:
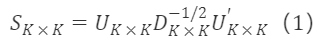
對稱正交的性質:
- 與施密特正交相比,對稱正交不需要提供正交次序,對每個因子是平等看待的
- 在所有正交過渡矩陣中,對稱正交後的矩陣和原始矩陣的相似性最大,即正交前後矩陣的距離最小。
# 對稱正交
def Symmetry(factors):
col_name = factors.columns
D, U = np.linalg.eig(np.dot(factors.T, factors))
U = np.mat(U)
d = np.diag(D**(-0.5))
S = U*d*U.T
#F_hat = np.dot(factors, S)
F_hat = np.mat(factors)*S
factors_orthogonal = pd.DataFrame(F_hat, columns=col_name, index=factors.index)
return factors_orthogonal
res = Symmetry(f)
關於LUCIDA \& FALCON
Lucida (https://www.lucida.fund/ )是行業領先的量化對沖基金,在2018年4月進入Crypto市場,主要交易CTA / 統計套利 / 期權波動率套利等策略,現管理規模3000萬美元。
Falcon (https://falcon.lucida.fund /)是新一代的Web3投資基礎設施,它基於多因子模型,幫助用戶"選"、"買"、"管"、"賣"加密資產。Falcon在2022年6月由Lucida所孵化。









