零知識證明的力量：深入理解 zk-SNARK

編譯：DODO Research

作者：0xAlpha Co-founder @DeriProtocol

介紹

zk-SNARK，即"零知識簡潔非互動式知識論證"，使得一名驗證者能夠確認一名證明者擁有某些特定知識，這些知識被稱為 witness，滿足特定的關係，而無需透露關於見證本身的任何信息。

• 為特定問題生成 zk-SNARK 包括以下四個階段：
• 將問題（或函數）轉換成算術門電路。
• 然後將這個電路翻譯成矩陣公式。
• 這個矩陣公式進一步轉換成一個多項式，這個多項式應該能被一個特定的最小多項式整除。

最後，這種可整除性在有限域的橢圓曲線點中表示出來，證明就在這裡進行。

前三個步驟僅僅是轉換了原始陳述的表示方式。最後一個步驟使用同態加密將第三步的陳述投影到加密空間中，使得證明者能夠證實其中的鏡像陳述。鑑於這種投影利用了非對稱加密，從第三步的陳述回溯到原始陳述是不可行的，確保了零知識的暴露。

閱讀本文所需的數學背景相當於 STEM 專業學生的大一級代數水平。唯一可能具有挑戰性的概念可能是橢圓曲線加密。對於不熟悉這一點的人來說，可以將其視為具有特殊基數的指數函數，同時要記住其逆函數仍然未解。

本文將遵循以下符號規則：

矩陣：粗體大寫字母，例如A ；顯式形式寫作
向量：帶箭頭的小寫字母，顯式形式寫作[ ] ；默認情況下所有向量均為列向量
標量：常規字母表示

讓我們用這個問題作為例子：

f(x)=x\^3+x\^2+5 (1)

假設愛麗絲想要證明她知道一個 。我們將逐步介紹愛麗絲為她的證明生成 zk-SNARK 所需採取的整個程序。
這個問題可能看起來太簡單，因為它不涉及控制流（例如，if-then-else）。然而，將帶有控制流的函數轉換為算術表達式並不困難。例如，讓我們考慮以下問題（或在編程語言中的"函數"）：

f(x, z):
if(z==1):
return x*x*x+x*x+5
else:
return x*x+5

將這個問題重寫為以下算術表達式很容易（假設z屬於(0,1) ），這並不比方程式 (1) 複雜多少。

f(x,z)=(z-1)(x\^2+5)+z(x\^3+x\^2+5)

在本文中，我們將繼續使用方程式 (1) 作為討論的基礎。

第1步：算術門電路

方程式 (1) 可以分解為以下基本算術運算：

這對應於以下算術門電路：

我們還將方程式 (2) 稱為一組4個"一級約束"，每個約束描述了電路中一個算術門的關係。通常，一組 n 個一級約束可以概括為一個二次算術程序（QAP），接下來將進行解釋。

第2步：矩陣

首先，讓我們定義一個"見證"向量，如下所示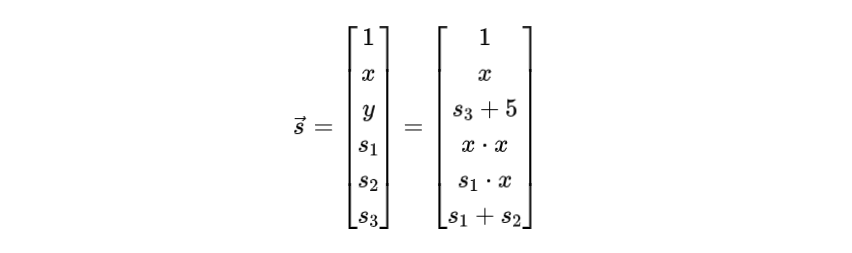：其中y, s1,s2,s3 與方程式 (2) 中定義的相同。
通常，對於一個有m個輸入和n個算術門的問題（即 n-1 個中間步驟和最終輸出），這個見證向量將是(m+n+1)維的。在實際問題中，數字n可能非常大。例如，對於哈希函數，n通常是幾千。

接下來，讓我們構造三個 n*(m+n+*1) 矩陣A,B,C，以便我們可以將方程式 (2) 重寫如下：

方程式 (3) 只是方程式 (2) 的另一種表示形式：每組(ai,bi,ci)對應於電路中的一個門。我們只需要明確地展開矩陣公式就可以看到這一點：

所以LHS=RHS與方程式 (2) 完全相同，矩陣方程的每一行對應一個一級約束（即電路中的一個算術門）。

我們跳過了構建(A,B,C) 的步驟，其實這些步驟相對簡單直接。我們只需要根據相應的一級約束，把它們轉換成矩陣形式，從而確定(A,B,C) 每一行的內容，即(ai,bi,ci)。以第一行為例：可以很容易地看出，要使第一個一級約束 x與x 相乘等於 s1 成立，我們需要的是將[0,1,0,0,0]、[0,1,0,0,0] 和[0,0,0,1,0,0]與向量s相乘。

因此，我們已經成功地把算術門電路轉換成了矩陣公式，即方程式 (3)。同時，我們也把需要證明掌握的對象，從轉變為了見證向量s。

第3步：多項式

現在，讓我們構造一個 n*(*n+m+*1) 矩陣PA，它定義了一組關於z的多項式：

這些是六個變量的四組線性方程，可以用傳統方法求解。然而，在這種情況下解決 PA 的更有效方法是拉格朗日插值，它利用了問題的特殊性。這裡我們跳過求解 PA 的過程，雖然有點繁瑣但很直接。

其中：

第4步：橢圓曲線點

將方程式 (4) 重寫為：

其中i(z)=1只是z的一個平凡的零次多項式，用來使方程統一------所有項都是二次的。這樣做的必要性很快就會變得清晰。注意這個方程只包含z的多項式的加法和乘法。

接下來，我們將更詳細地闡述實際的操作步驟。

橢圓曲線加密

橢圓曲線的一般理論遠遠超出了本文的範圍。就本文的目的而言，橢圓曲線被定義為從素域Fp映射到E函數，其中E包括滿足y\^2=x\^3+ax+b的點（稱為橢圓曲線點，簡稱 ECPs）。

請注意，雖然到目前為止我們一直在討論常規算術，但現在當我們轉換到素域時，數字的算術運算是以模運算的方式進行的。例如a+b=a+b(mod p)，其中p是Fp的階。

另一方面，兩個橢圓曲線點的加法定義如下圖所示：

具體來說，兩個 ECPs P和Q的加法：

找到直線PQ和曲線R的交點，定義為-(P+Q)
翻轉到曲線上R的"鏡像"點R'。
因此我們定義橢圓曲線點的加法P+Q=R'：

請注意，這個規則也適用於特殊情況，即一個 ECP 自加的情況，此時將使用該點的切線。

現在假設我們隨機選擇一個點G，並將數字1映射到它上面。（這種"初始映射"聽起來有點任意。稍後將進行討論）。然後對於任n 屬於Fp，我們定義：

E(N)=G+ G+ G+ …..+G=G點乘n

這有一個操作表達式。定義+G的操作為"生成器"，記為g。那么上述定義等同於：

對於不熟悉橢圓曲線的人來說，你可以將這種映射類比為一個常規的指數函數，其中基數g代替了實數。算術運算的行為類似。然而，一個關鍵的區別是g\^n的逆函數在計算上是不可行的。也就是說，沒有辦法計算橢圓曲線版本的。這當然是橢圓曲線加密的基礎。這樣的映射被稱為單向加密。

請注意，給定一個橢圓曲線，由於選擇G（因此選擇"生成器" g）是任意的（除了 x 軸上的點），有無限種映射方式。選擇（G或 g）可以類比為選擇指數函數的基數（2\^x,10\^x,e\^x等），這是常識的一部分。

然而，Alice 想要證明的方程式 (5) 是二次形式的，所以線性不夠。為了處理二次項，我們需要在加密空間中定義乘法。這被稱為配對函數 ，或雙線性映射 ，接下來將進行解釋。

雙線性映射

公共參考字符串

整個過程被稱作"驗證鑰"，簡稱VK。這裡只涉及7個橢圓曲線點（ECPs），需要提供給驗證方。要注意的是，不管問題裡面涉及多少輸入和一級約束，VK始終是由7個ECPs構成的。

另外，值得一提的是，"可信設置"以及生成PK和VK的過程，對於一個特定的問題來說，只需操作一次即可。

證明與驗證

現在擁有公鑰（PK），愛麗絲將計算以下橢圓曲線點（ECPs）：

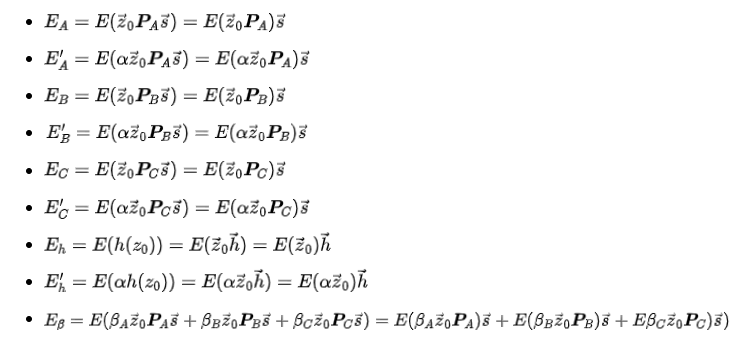
這9個橢圓曲線點就是零知識簡潔非互動式證明（zk-SNARK）的關鍵！

注意，愛麗絲其實只是對公鑰裡的橢圓曲線點做了些線性組合運算。這點特別關鍵，驗證時會重點檢查。

現在，愛麗絲交出了zk-SNARK證明，咱們終於進入驗證環節，分三步走。

首先得確認，前8個橢圓曲線點真的是通用參考串裡那些點的線性組合。

如果這三項檢查都成立，那麼等式（5）得到驗證，因此我們相信愛麗絲知道見證。讓我們解釋一下等式背後的理由。以第一部分中的第一個等式為例，等式成立是因為雙線性性質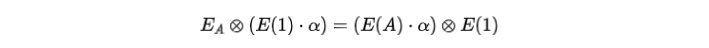：然而，由於愛麗絲不知道符號阿拉法的值，她無法明確計算這個加法。她唯一能想出來滿足等式的一對(EA,EA')的方法，是分別用相同的一組向量s ，計算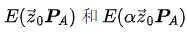的兩個組合。

參考文獻

"Zk-SNARKs: Under the Hood" (Vitalik Buterin)

"A Review of Zero Knowledge Proofs" (Thomas Chen, Abby Lu, Jern Kunpittaya, and Alan Luo)

"Why and How zk-SNARK Works: Definitive Explanation" (Maksym Petkus)

Website: Zero-Knowledge Proofs

Wikipedia: Elliptic curve

Wikipedia: Finite field

Wikipedia: Pairing-based cryptography