3.1 비밀 엔진

각 제로 지식 증명 시스템이 두 부분으로 구성되어 있다는 것을 인식합니다: 하나는 알고리즘이고, 다른 하나는 다항식 약속 계획입니다. 프로그램을 제로 지식 증명(ZKP)으로 변환하는 초기 단계는 알고리즘과 관련이 있습니다. 이 과정은 이러한 다항식 간의 특정 조건을 설정하여 그들 간의 관계를 명확히 합니다.

우리의 제로 지식 증명 시스템은 표준 PlonK 레시피를 기반으로 구현되었으며, 고도로 사용자 정의된 게이트를 포함하고 있습니다. 주요 내용은 다음과 같습니다:

• 도구: 기본 산술 회로, 해시, ECC, zkshuffle, zkmatchmaking 등 게임 회로 개발에 사용되는 다양한 도구를 지원합니다. 이러한 도구에 대한 더 많은 정보를 얻으려면 우리의 GitHub 저장소를 방문하는 것이 좋습니다.

• 온체인 검증기: 증명자와 검증자를 위해 PLONK/ZKVM을 최적화했으며, 모든 EVM 체인의 일반 신뢰성 검증기를 지원합니다.

• 응용 프로그램 특정 Plonk: 응용 프로그램 특정 Plonk를 기본 ZK 증명으로 사용하고, 우리의 SDK에서 제공하는 다양한 도구를 사용하여 특정 게임 회로를 작성합니다. 또한 우리는 다양한 블록체인 시스템에서 실행할 수 있는 다양한 가상 머신(EVM/WASM/…)에서 검증 계약을 제공합니다. 이를 통해 오프체인 증명과 온체인 검증을 구현합니다.

다음으로, Secret Engine에서 개발된 두 가지 중요한 구성 요소인 zkshuffle와 zkmatchmaking을 소개합니다.

3.1.1 ZK 셔플 SDK

3.1.1.1 소개

포커 게임은 매우 인기 있는 카드 게임입니다. 현실 세계에서 게임의 각 당사자는 게임의 공정성을 보장하기 위해 서로를 감독할 수 있습니다. 컴퓨터 네트워크의 빠른 발전으로 네트워크에 연결된 플레이어도 포커 게임에 참여할 수 있는 기회를 가지게 되었지만, 네트워크 환경에서 게임이 원활하게 진행되고 공정성을 보장하는 것은 큰 도전 과제가 되었습니다. 이것이 심리 포커 프로토콜이 해결해야 할 문제입니다.

심리 포커는 암호학 원리를 기반으로 구성된 포커 게임으로, 1979년 Shamir, Rivest, Adleman이 첫 번째 심리 포커 프로토콜을 제안한 이후로 사람들은 심리 포커 게임의 가능성을 연구하기 시작했습니다. 심리 포커는 일반 포커와 유사한 방식으로 진행되지만, 주요 차이점은 심리 포커가 물리적 카드 없이 네트워크 환경에서 진행되며, 모든 플레이어가 기본적으로 불성실하다고 가정합니다. 즉, 부정행위가 존재합니다. 첫 번째 심리 포커 프로토콜은 두 당사자 간의 포커 프로토콜로, 보안 취약점이 존재하는 것으로 입증되었습니다. 문헌에 따르면, 공정한 심리 포커는 다음 속성을 충족해야 합니다:

1. 유일성: 전통적인 포커 게임에서는 카드가 중복되지 않도록 명시적으로 카드를 보여줍니다. 심리 포커 프로토콜도 동일한 특성을 보장해야 합니다.

2. 무작위 분포: 전통적인 포커 게임에서는 한 플레이어가 카드를 섞고, 다른 플레이어는 이를 실시간으로 관찰할 수 있습니다. 이는 섞는 플레이어가 최종 섞기 결과를 제어할 수 없음을 의미합니다.

3. 비밀성: 카드 더미가 아래로 향해 있을 때는 카드 더미에 있는 카드에 대한 정보를 공개해서는 안 됩니다. 또한, 플레이어가 카드를 뽑을 때 다른 플레이어는 해당 카드에 대한 정보를 얻을 수 없습니다.

4. 신뢰할 수 있는 제3자가 없음: 신뢰할 수 있는 제3자에 의존하는 것은 불가능합니다. 왜냐하면 누구든지 매수될 수 있으며, 절대적으로 신뢰할 수 있는 제3자는 존재하지 않기 때문입니다.

1987년, Crépeau는 첫 번째 안전한 심리 포커 프로토콜을 제안했습니다. 이후 심리 포커 프로토콜이 등장하기 시작했지만, 많은 심리 포커 프로토콜 연구는 TTP를 기반으로 하고 있습니다. 학계에서는 TTP를 사용하는 것이 심리 포커 프로토콜의 공정성을 해결하는 효과적인 방법으로 널리 인식되고 있습니다. 그러나 포커는 오락 및 여가 게임으로서 많은 상황에서 제3자가 존재하지 않으며, 제3자의 신뢰성을 보장하기가 어렵습니다. 특히 블록체인 기술이 관련된 경우에는 일반적으로 신뢰할 수 있는 제3자가 존재하지 않기 때문에, PPT 없이 공정한 심리 포커 프로토콜을 구현하는 것이 중요합니다. Barnett-Smart 프로토콜은 2003년에 제안되었으며, ElGamal 및 Pailler 암호 시스템을 기반으로 두 가지 솔루션을 제공합니다. 그러나 Pailler 암호화 계획에는 보안 한계가 있으며, 이는 공모 인원이 (N-1)/2를 초과하지 않는다는 가정에 기반합니다. 이후 Castellà-Roca 프로토콜이 제안되었으며, 이는 다른 암호화 계획을 사용하고, 셔플 과정이 Barnett-Smart 프로토콜보다 빠릅니다.

심리 포커 프로토콜의 오버헤드는 주로 셔플 부분에 집중되어 있지만, 오늘날 제로 지식 증명 알고리즘이 빠르게 발전함에 따라, geometry는 셔플 과정이 더 이상 병목 현상이 아니라고 지적합니다. geometry는 Barnett-Smart 프로토콜이 완전한 카드 게임 프로토콜을 여러 개의 안전한 하위 프로토콜로 나누어야 한다고 생각합니다: 카드 생성, 마스킹, 재마스킹, 셔플 등. 이러한 단계는 쉽게 플러그 앤 플레이로 구현할 수 있으며, 그 보안 가정은 결정적 Diffie-Hellman에 기반합니다. 따라서 우리의 멘탈 포커 프로토콜은 주로 Barnett-Smart 프로토콜을 참조하지만, 동시에 한 세트의 포커 카드에 대해 zkShuffle을 수행하는 데 많은 타원 곡선 연산이 필요하다는 점도 고려합니다. 이로 인해 회로 규모가 상당히 커질 수 있습니다. 이 문제를 해결하기 위해, 우리는 zkshuffle에 친화적인 TurboPlonk 알고리즘을 재설계하여 회로 게이트의 규모를 크게 줄였습니다.

3.1.1.2 기본 개념

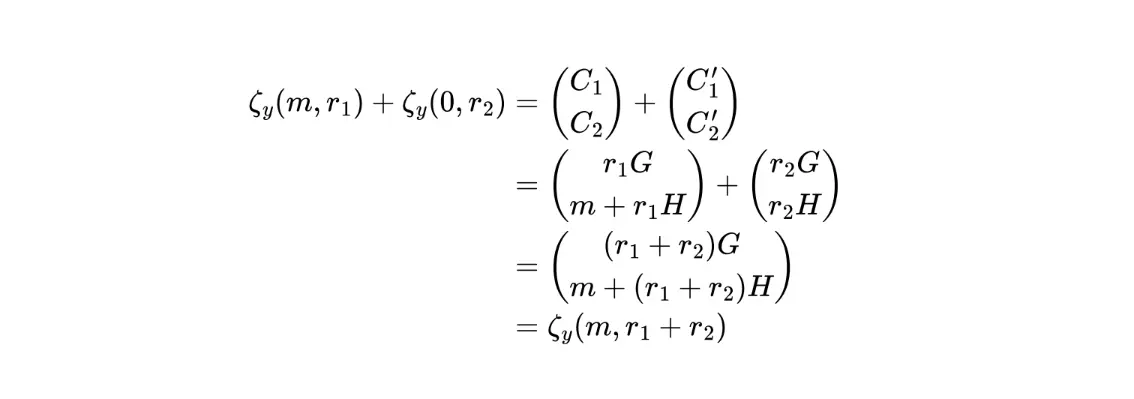
주: n-out-of-n 임계값 EIGamal 암호화

3.1.1.3 심리 포커 프로토콜

멘탈 포커 프로토콜은 하나의 프로토콜이 아니라, 각 행동을 담당하는 일련의 하위 프로토콜로 구성됩니다.

• 키 생성:

• 각 플레이어에 대해 공개 및 개인 키 쌍을 생성합니다.
• 모든 플레이어의 공개 키를 집계하여 하나의 공개 키를 생성합니다.

• 마스킹:

• 마스킹 함수는 집계된 공개 키 하의 ElGamal 암호화 함수입니다.

• 셔플 및 재마스킹:

• 카드를 무작위화하기 위해 셔플 작업을 수행합니다.
• 셔플된 카드에 대해 다시 마스킹을 수행합니다.

• 언마스크:

• 카드를 디코딩하여 실제 카드 정보를 얻습니다.

키 생성 프로토콜

마스킹 프로토콜

재마스킹 프로토콜

셔플 인수

언마스크 프로토콜

3.1.1.4 셔플 친화적 PLONK 알고리즘

셔플 프로토콜은 주로 두 부분으로 구성됩니다: 1) 카드의 치환; 2) 카드의 재마스킹. 이 중 재마스킹 작업은 타원 곡선 연산을 포함하며, 구체적으로는 1개의 상수 기반 스칼라 곱셈, 1개의 비상수 기반 스칼라 곱셈 및 2개의 곡선 추가가 포함됩니다. 비최적화된 TurboPlonk 사용자 정의 게이트를 사용하여 산술 회로를 작성할 경우, 한 장 카드의 재마스킹 회로 게이트 수는 596+1622+2=2220이 됩니다. 따라서 전체 카드 세트(52장)의 경우 회로 게이트 수는 115440에 이를 것이며, 이는 치환 관련 회로를 포함하지 않은 수치입니다. 따라서 비최적화된 TurboPlonk를 사용하여 산술 회로를 작성할 경우, 셔플 시간은 매우 길어질 것입니다. 이 문제를 해결하기 위해, 우리는 TurboPlonk를 재설계하여 셔플 연산에 친화적으로 만들었으며, 검증 결과 재마스킹 작업에 대해서는 단 85개의 게이트만 필요합니다.

주: bowe hopwood

3.1.1.5 온체인 검증

또한, 우리의 실천에서 우리는 온체인 검증 가스 비용이 높은 문제를 겪었습니다. 여기서는 주로 우리의 최적화 경험을 공유하겠습니다.

Verify reveal은 한 장 카드를 복호화하는 데 다른 플레이어가 해당 카드의 개봉 정보를 제공해야 하며, 동시에 개봉의 정확성을 검증하기 위한 증명을 제공해야 합니다. 현재 Geometry의 현실은 chaum pedersen 프로토콜을 기반으로 개봉 증명을 구성하였으며, chaum pedersen은 점 곱셈 연산이 필요합니다. 점 곱셈 작업은 매우 비쌉니다. 이는 현재 이더리움이 Baby Jubjub 곡선의 사전 컴파일 계약을 지원하지 않기 때문입니다. 테스트 결과에 따르면, Geometry를 기반으로 한 개봉 증명의 가스 비용은 7629888에 달하며, 이는 명백히 수용할 수 없습니다.

Baby Jubjub이 BN254의 내장 곡선이라는 점을 고려할 때, 우리는 Snark를 사용하여 개봉 증명을 수행할 수 있습니다. 가스 분석에 따르면, Groth16을 사용하여 개봉 증명의 온체인 검증 비용은 약 200k에 불과하며, 이는 원래 검증 방식보다 30배 이상 감소한 수치입니다. 원래 검증 방식에 비해 이는 매우 좋은 선택으로 보이며, 개봉 회로는 다음과 같습니다:

미래에는 우리는 증명 집합을 통해 가스를 더 많이 절약할 계획입니다.

Verify shuffle에서는 텍사스 홀덤 게임에서 셔플된 결과를 온체인에 저장해야 합니다. 이는 현재의 셔플 결과로 사용될 뿐만 아니라 후속 셔플 회로의 공개 입력으로도 사용됩니다. 그러나 한 세트의 포커 카드에는 52장이 있으며, 총 208개의 uint256 유형 데이터가 존재하여 온체인 저장 비용이 비쌉니다.

우리의 해결책은 온체인에 일부 포커 카드 데이터만 저장하는 것입니다. 구체적으로, 우리는 2n+5장의 카드만 저장하면 됩니다. 여기서 n은 플레이어 수입니다. 우리의 게임은 최대 6명의 플레이어를 지원하므로 최대 17장의 카드만 사용됩니다. 이는 결국 온체인에 17장의 카드만 저장하면 된다는 것을 의미하며, 2/3의 저장 비용을 절감할 수 있습니다.

결국 우리는 온체인에 17장의 카드만 저장하면 되지만, 앞서 언급한 온체인 저장의 또 다른 목적은 이러한 카드가 후속 셔플 회로의 공개 입력으로 사용될 것이라는 점입니다. 따라서 17장의 카드만 저장하면 셔플의 정확성을 검증할 수 없습니다. 이 문제를 해결하기 위해, 셔플 회로는 전체 포커 카드의 해시 값을 추가로 출력하여 온체인에 저장합니다. zkShuffle을 검증할 때, 이는 회로의 공개 입력으로 사용되어 셔플의 정확성을 보장합니다.

3.1.2 ZK 매치메이킹 SDK

매치메이킹은 플레이어의 수준에 따라 게임을 매칭하여 플레이어가 실력에 맞는 상대와 대결할 수 있도록 보장하는 메커니즘입니다. 이를 통해 공정하고 재미있는 게임 경험을 제공합니다. 매치메이킹의 핵심 목표는 다음 두 가지로 요약할 수 있습니다:

• 공정한 대결: 실력이 비슷한 플레이어 간의 대결을 제공하여 양측의 승리 확률이 최대한 50%에 가깝도록 합니다.

• 예측 불가능성: 매칭 과정은 예측할 수 없으며, 최종 대결의 선수도 예측할 수 없습니다.

전체 프로세스

1. Prover가 되기 위해 신청할 때, 계약에 하나의 시드를 약속해야 하며, 이 시드는 오직 Prover만 알고 있습니다.

2. 플레이어가 게임 참여 요청을 보냅니다.

3. 정렬기가 요청을 수신한 후, 등급 전략에 따라 정렬하고, 생성된 큐를 계약과 증명자에게 각각 보냅니다.

4. Prover는 zkSnark를 기반으로 서로 다른 큐를 무작위로 매칭하며, 매칭 결과는 Prover가 약속한 시드, 입력 큐 및 온체인 난수(확정적이지만 예측 불가능한)에 따라 달라집니다. 그런 다음 매칭 결과와 증명을 계약에 보냅니다.

5. 계약은 온체인 검증을 수행하며, 검증이 통과하면 플레이어는 매칭 결과에 따라 게임에 들어갑니다.

블록체인에서는 block hash와 같은 온체인 난수를 쉽게 얻을 수 있지만, 이는 채굴자와 검증자의 블록 보류 공격을 받을 수 있어 block hash와 같은 온체인 난수가 충분히 안전하지 않으며, 매치메이킹의 예측 불가능성도 도전받을 수 있습니다. 검증 가능한 난수 함수(VRF)는 검증 특성을 가진 난수 생성기로, 통계적으로 균일하고 예측할 수 없는 난출을 생성할 수 있으며, 그 출력은 검증 가능합니다. 이는 우리의 온체인 난수에 대한 훌륭한 해결책을 제공합니다. VRF의 원리를 간단히 살펴보면, 입력으로 시드를 받고, 출력으로 난수를 생성합니다.

온체인 난수 외에도 예측 불가능성은 Prover가 약속한 시드에 의존합니다. 우리는 Prover가 임의로 난수를 유출하지 못하도록 처벌 메커니즘을 구축할 것입니다.

참고 문헌:

【15】A. Shamir, R. L. Rivest and L. M. Adleman, Mental poker, Technical report LCS/TM-125, Massachusetts Institute of Technology, April 1979.
【16】Crépeau C. A secure poker protocol that minimizes the effect of player coalitions, in: Conference on the Theory and Application of Cryptographic Techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 1985: 73--86.
【17】C. Crepeau, A zero-knowledge poker protocol that achieves confidentiality of the players' strategy or how to achieve an electronic poker face, in: Advances in Cryptology -- Crypto 086, Lecture Notes in Computer Science 263, Springer-Verlag, Berlin (1987), 239--247.
【18】A. Barnett and N. Smart, Mental poker revisited, in: Cryptography and Coding, Lecture Notes in Computational Science 2898, Springer-Verlag, Berlin (2003), 370--383.
【19】J. Castellà-Roca, Contributions to mental poker, Ph.D. Thesis, Autonomous University of Barcelona, Doctoral Programme in Computer Science and Artificial Intelligence, 2005.
【20】N Mohnblatt, A Novakovic and K Gurkan, Mental Poker in the Age of SNARKs - Part 1,
https://geometry.xyz/notebook/mental-poker-in-the-age-of-snarks-part-1
【21】N Mohnblatt, A Novakovic and K Gurkan, Mental Poker in the Age of SNARKs - Part 1,
https://geometry.xyz/notebook/mental-poker-in-the-age-of-snarks-part-2
【22】Gabizon A, Williamson Z J. The turbo-plonk program syntax for specifying snark programs, in: ZKProof Workshop. 2020, 3.
【23】Desmedt Y. Threshold cryptosystems, in: International Workshop on the Theory and Application of Cryptographic Techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 1992: 1--14.
【24】https://github.com/arkworks-rs/crypto-primitives/tree/main/crypto-primitives/src/crh/bowe_hopwood.

【25】https://github.com/geometryxyz/mental-poker/blob/main/barnett-smart-card-protocol/src/discretelogcards/mod.rs#L320.

【26】Todd Norton, Groth16 Verification Gas cost,https://hackmd.io/@nebra-one/ByoMB8Zf