LUCIDA & FALCON：다중 요인 전략을 사용하여 강력한 암호 자산 포트폴리오 구축

저자：LUCIDA \& FALCON

서문

이전 글에서 우리는 《다중 요인 전략으로 강력한 암호 자산 투자 포트폴리오 구축하기》 시리즈의 첫 번째 글인 --- 이론 기초 편을 발표했습니다. 이번 글은 두 번째 편 --- 데이터 전처리 편입니다.

요인 데이터를 계산하기 전/후 및 단일 요인의 유효성을 테스트하기 전에 관련 데이터를 처리해야 합니다. 구체적인 데이터 전처리에는 중복 값, 이상 값/결측 값/극단 값, 표준화 및 데이터 빈도 처리가 포함됩니다.

1. 중복 값

데이터 관련 정의：

• 키（ Key ）：독특한 인덱스를 나타냅니다. 예를 들어, 모든 토큰의 모든 날짜에 대한 데이터에서 키는 "tokenid/contractaddress - 날짜"입니다.
• 값（ Value ）：키로 인덱싱된 객체를 "값"이라고 합니다.

중복 값을 진단하기 위해서는 데이터가 "어떻게" 되어야 하는지를 이해해야 합니다. 일반적으로 데이터의 형태는 다음과 같습니다:

1. 시계열 데이터（ Time Series ）。키는 "시간"입니다. 예를 들어, 단일 토큰의 5년 가격 데이터입니다.
2. 단면 데이터（ Cross Section ）。키는 "개체"입니다. 예를 들어, 2023.11.01일의 모든 암호화폐 시장 토큰 가격 데이터입니다.
3. 패널 데이터（ Panel ）。키는 "개체-시간"의 조합입니다. 예를 들어, 2019.01.01-2023.11.01 4년 동안의 모든 토큰 가격 데이터입니다.

원칙：데이터의 인덱스(키)를 결정하면 데이터가 어떤 수준에서 중복 값이 없어야 하는지를 알 수 있습니다.

검사 방법：

1. pd.DataFrame.duplicated(subset=[key1, key2, …])

   중복 값의 수를 확인합니다: pd.DataFrame.duplicated(subset=[key1, key2, …]).sum()

   중복 샘플을 추출하여 확인합니다: df[df.duplicated(subset=[…])].sample() 샘플을 찾은 후, df.loc를 사용하여 해당 인덱스에 해당하는 모든 중복 샘플을 선택합니다.

2. pd.merge(df1, df2, on=[key1, key2, …], indicator=True, validate='1:1')

   수평 병합 함수에 indicator 매개변수를 추가하면 merge 필드가 생성됩니다. 이를 사용하여 dfm['merge'].value_counts()로 병합 후 서로 다른 출처의 샘플 수를 확인할 수 있습니다.

   validate 매개변수를 추가하면 병합된 데이터 세트의 인덱스가 예상대로(1:1, 1:다수 또는 다수:다수)인지 검증할 수 있습니다. 마지막 경우는 사실 검증이 필요 없는 경우입니다. 예상과 다르면 병합 과정에서 오류가 발생하고 실행이 중단됩니다.

2. 이상 값/결측 값/극단 값

이상 값이 발생하는 일반적인 원인：

1. 극단적인 상황. 예를 들어, 토큰 가격이 0.000001$이거나 시가총액이 50만 달러에 불과한 토큰은 조금만 변동해도 수십 배의 수익률을 얻을 수 있습니다.

2. 데이터 특성. 예를 들어, 토큰 가격 데이터가 2020년 1월 1일부터 다운로드되었다면, 자연스럽게 2020년 1월 1일의 수익률 데이터를 계산할 수 없습니다. 이전 날의 종가가 없기 때문입니다.

3. 데이터 오류. 데이터 제공자가 실수를 할 수 있습니다. 예를 들어, 12원당 토큰을 1.2원당 토큰으로 기록하는 경우입니다.

이상 값 및 결측 값 처리 원칙：

1. 삭제. 합리적으로 수정할 수 없는 이상 값은 삭제를 고려할 수 있습니다.

2. 대체. 일반적으로 극단 값 처리에 사용됩니다. 예를 들어, 윈저화(Winsorizing) 또는 로그 변환(비정상적 사용)입니다.

3. 채우기. 결측 값에 대해서도 합리적인 방법으로 채우는 것을 고려할 수 있습니다. 일반적인 방법으로는 평균(또는 이동 평균), 보간(Interpolation), 0으로 채우기 df.fillna(0), 앞으로 채우기 df.fillna('ffill')/뒤로 채우기 df.fillna('bfill') 등이 있습니다. 채우기에 의존하는 가정이 적합한지 고려해야 합니다.

   머신러닝에서는 뒤로 채우기를 신중하게 사용해야 하며, Look-ahead bias의 위험이 있습니다.

극단 값 처리 방법：

1. 백분위법.

순서를 오름차순으로 정렬하여 최소 및 최대 비율을 초과하는 데이터를 임계 데이터로 대체합니다. 역사적 데이터가 풍부한 경우 이 방법은 상대적으로 거칠며, 고정 비율의 데이터를 강제로 삭제하면 일정 비율의 손실이 발생할 수 있습니다.

2. 3σ / 삼배 표준 편차법

표준 편차 σfactor는 요인 데이터 분포의 분산 정도, 즉 변동성을 나타냅니다. μ±3×σ 범위를 이용하여 데이터 세트의 이상 값을 식별하고 대체합니다. 약 99.73%의 데이터가 이 범위에 포함됩니다. 이 방법의 적용 전제: 요인 데이터는 정규 분포를 따라야 합니다 즉, X∼N(μ,σ²).

여기서, μ=∑ⁿᵢ₌₁⋅ Xi / N , σ²=∑ⁿᵢ₌₁=( xi -μ)²/ n , 요인 값의 합리적인 범위는 [μ−3×σ,μ+3×σ]입니다.

데이터 범위 내의 모든 요인에 대해 다음과 같은 조정을 수행합니다:

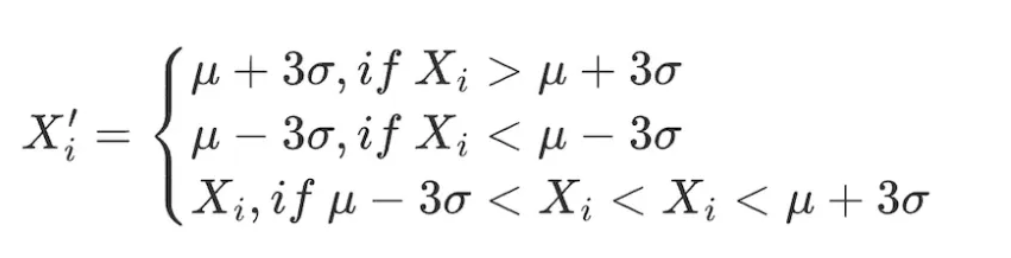이 방법의 단점은, 정량화 분야에서 일반적으로 사용되는 데이터인 주식 가격, 토큰 가격 등이 종종 뾰족한 두꺼운 꼬리 분포를 보이며 정규 분포 가정을 따르지 않는다는 것입니다. 이 경우 3σ 방법을 사용하면 많은 데이터가 잘못된 이상 값으로 식별될 수 있습니다.

3. 절대값 차 중위수법 (Median Absolute Deviation, MAD)

이 방법은 중위수와 절대 편차를 기반으로 하여 처리된 데이터가 극단 값이나 이상 값에 덜 민감하게 만듭니다. 평균 및 표준 편차 기반 방법보다 더 견고합니다.

절대 편차의 중위수 MAD = median(∑ⁿᵢ₌₁(Xi - Xmedian))

요인 값의 합리적인 범위는 [Xmedian - n × MAD, Xmedian + n × MAD]입니다. 데이터 범위 내의 모든 요인에 대해 다음과 같은 조정을 수행합니다:

# 요인 데이터의 극단 값 처리
class Extreme(object):
    def __init__(s, ini_data):
        s.ini_data = ini_data

    def three_sigma(s, n=3):
        mean = s.ini_data.mean()
        std = s.ini_data.std()
        low = mean - n * std
        high = mean + n * std
        return np.clip(s.ini_data, low, high)

    def mad(s, n=3):
        median = s.ini_data.median()
        mad_median = abs(s.ini_data - median).median()
        high = median + n * mad_median
        low = median - n * mad_median
        return np.clip(s.ini_data, low, high)

    def quantile(s, l=0.025, h=0.975):
        low = s.ini_data.quantile(l)
        high = s.ini_data.quantile(h)
        return np.clip(s.ini_data, low, high)

3. 표준화

1. Z-점수 표준화

• 전제：X N (μ，σ)
• 표준 편차를 사용하기 때문에 이 방법은 데이터의 이상 값에 민감합니다.

x'ᵢ=(x−μ)/σ=(X−mean(X))/std(X)

2. 최대 최소값 차 표준화 (Min-Max Scaling)

각 요인 데이터를 (0,1) 구간의 데이터로 변환하여 서로 다른 규모나 범위의 데이터를 비교할 수 있도록 하지만, 데이터 내부의 분포를 변경하지 않으며 총합이 1이 되지 않습니다.

• 극대 극소 값을 고려하기 때문에 이상 값에 민감합니다.
• 단위를 통일하여 서로 다른 차원의 데이터를 비교하기 용이합니다.

x'ᵢ=(xᵢ−min(x))/(max(x)−min(x))

3. 순위 백분위 (Rank Scaling)

데이터 특성을 순위로 변환하고 이 순위를 0과 1 사이의 점수로 변환합니다. 일반적으로 데이터 세트 내에서의 백분위수입니다.*

• 순위는 이상 값의 영향을 받지 않기 때문에 이 방법은 이상 값에 민감하지 않습니다.

• 데이터 내 각 점 간의 절대 거리를 유지하지 않고 상대 순위로 변환합니다.

NormRankᵢ=(Rankₓᵢ−min(Rankₓ))/(max(Rankₓ)−min(Rankₓ))=Rankₓᵢ/N

여기서, min(Rankₓ)=0, N은 구간 내 데이터 포인트의 총 개수입니다.

# 요인 데이터 표준화
class Scale(object):
    def __init__(s, ini_data, date):
        s.ini_data = ini_data
        s.date = date

    def zscore(s):
        mean = s.ini_data.mean()
        std = s.ini_data.std()
        return s.ini_data.sub(mean).div(std)

    def maxmin(s):
        min = s.ini_data.min()
        max = s.ini_data.max()
        return s.ini_data.sub(min).div(max - min)

    def normRank(s):
        # 지정된 열에 대해 순위를 매깁니다. method='min'은 동일한 값이 동일한 순위를 갖도록 하며 평균 순위를 사용하지 않습니다.
        ranks = s.ini_data.rank(method='min') 
        return ranks.div(ranks.max())

4. 데이터 빈도

때때로 얻은 데이터는 우리가 분석에 필요한 빈도가 아닙니다. 예를 들어, 분석 수준이 월별이고 원시 데이터의 빈도가 일별인 경우 "다운 샘플링"을 사용하여 데이터를 월별로 집계해야 합니다.

다운 샘플링

하나의 집합의 데이터를 한 줄의 데이터로 집계하는 것을 의미합니다. 예를 들어, 일별 데이터를 월별로 집계합니다. 이때 집계되는 각 지표의 특성을 고려해야 하며, 일반적인 작업은 다음과 같습니다:

• 첫 번째 값/마지막 값
• 평균/중위수
• 표준 편차

업 샘플링

하나의 데이터 행을 여러 데이터 행으로 분할하는 것을 의미합니다. 예를 들어, 연간 데이터를 월별 분석에 사용하는 경우입니다. 이 경우 일반적으로 단순 반복으로 충분하며, 때때로 연간 데이터를 각 월에 비례하여 배분해야 합니다.

LUCIDA \& FALCON에 대하여

Lucida（https://www.lucida.fund/）는 업계 선도적인 양적 헤지 펀드로, 2018년 4월에 암호화폐 시장에 진입하였으며, 주로 CTA / 통계적 차익 거래 / 옵션 변동성 차익 거래 등의 전략을 거래하고 있으며, 현재 관리 규모는 3000만 달러입니다.

Falcon（https://falcon.lucida.fund）은 차세대 Web3 투자 인프라로, 다중 요인 모델을 기반으로 하여 사용자가 암호 자산을 "선택", "구매", "관리", "판매"할 수 있도록 돕습니다. Falcon은 2022년 6월 Lucida에 의해 인큐베이팅되었습니다.

더 많은 내용은 https://linktr.ee/lucida_and_falcon를 방문하세요.