제로 지식 증명의 힘: zk-SNARK 깊이 이해하기

编译：DODO Research

作者：0xAlpha Co-founder @DeriProtocol

소개

zk-SNARK, 즉 "제로 지식 간결 비대화형 증명"은 검증자가 특정 지식을 가진 증명자를 확인할 수 있게 해줍니다. 이 지식은 witness라고 불리며 특정 관계를 만족하지만, 증명 자체에 대한 정보는 공개하지 않습니다.

• 특정 문제에 대한 zk-SNARK 생성을 포함하는 네 가지 단계는 다음과 같습니다:
• 문제(또는 함수)를 산술 게이트 회로로 변환합니다.
• 그런 다음 이 회로를 행렬 공식으로 번역합니다.
• 이 행렬 공식은 특정 최소 다항식으로 나누어질 수 있는 다항식으로 변환됩니다.

마지막으로, 이러한 나눌 수 있는 성질은 유한체의 타원 곡선 점에서 나타나며, 증명이 여기서 이루어집니다.

첫 세 단계는 원래 진술의 표현 방식을 변환한 것에 불과합니다. 마지막 단계는 동형 암호화를 사용하여 세 번째 단계의 진술을 암호화된 공간으로 투영하여 증명자가 그 안의 거울 진술을 증명할 수 있게 합니다. 이러한 투영이 비대칭 암호화를 이용하기 때문에, 세 번째 단계의 진술에서 원래 진술로 되돌아가는 것은 불가능하여 제로 지식의 노출을 보장합니다.

이 문서를 읽기 위해 필요한 수학적 배경은 STEM 전공 학생의 1학년 대수 수준에 해당합니다. 유일하게 도전적일 수 있는 개념은 타원 곡선 암호화일 수 있습니다. 이에 익숙하지 않은 사람은 이를 특별한 기수의 지수 함수로 생각할 수 있으며, 그 역함수는 여전히 해결되지 않았음을 기억해야 합니다.

이 문서는 다음 기호 규칙을 따릅니다:

행렬: 굵은 대문자, 예: A; 명시적 형태로 작성
벡터: 화살표가 있는 소문자, 명시적 형태로 작성[ ]; 기본적으로 모든 벡터는 열 벡터입니다.
스칼라: 일반 문자로 표시

이 문제를 예로 들어 보겠습니다:

f(x)=x\^3+x\^2+5 (1)

앨리스가 그녀가 알고 있는 것을 증명하고 싶다고 가정해 보겠습니다. 우리는 앨리스가 그녀의 증명을 위해 zk-SNARK를 생성하는 데 필요한 전체 절차를 단계별로 소개할 것입니다.
이 문제는 제어 흐름(예: if-then-else)을 포함하지 않기 때문에 너무 간단해 보일 수 있습니다. 그러나 제어 흐름이 있는 함수를 산술 표현으로 변환하는 것은 어렵지 않습니다. 예를 들어, 다음 문제(또는 프로그래밍 언어의 "함수")를 고려해 보겠습니다:

f(x, z):
if(z==1):
return x*x*x+x*x+5
else:
return x*x+5

이 문제를 다음 산술 표현으로 다시 쓰는 것은 쉽습니다(가정: z는 (0,1) 에 속함). 이는 방정식 (1)보다 복잡하지 않습니다.

f(x,z)=(z-1)(x\^2+5)+z(x\^3+x\^2+5)

이 문서에서는 방정식 (1)을 논의의 기초로 계속 사용할 것입니다.

1단계: 산술 게이트 회로

방정식 (1)은 다음 기본 산술 연산으로 분해될 수 있습니다:

이는 다음 산술 게이트 회로에 해당합니다:

우리는 또한 방정식 (2)를 4개의 "1차 제약 조건" 집합이라고 부르며, 각 제약 조건은 회로의 하나의 산술 게이트의 관계를 설명합니다. 일반적으로 n개의 1차 제약 조건 집합은 이차 산술 프로그램(QAP)으로 요약될 수 있으며, 다음에서 설명할 것입니다.

2단계: 행렬

먼저 "증거" 벡터를 다음과 같이 정의합시다: 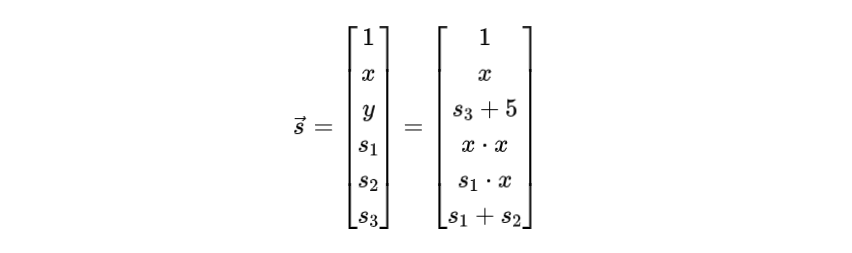여기서 y, s1, s2, s3는 방정식 (2)에서 정의된 것과 동일합니다.
일반적으로 m개의 입력과 n개의 산술 게이트가 있는 문제(즉, n-1개의 중간 단계와 최종 출력)에 대해 이 증거 벡터는 (m+n+1) 차원입니다. 실제 문제에서 n의 숫자는 매우 클 수 있습니다. 예를 들어, 해시 함수의 경우 n은 일반적으로 수천입니다.

다음으로, 우리는 방정식 (2)를 다음과 같이 다시 쓸 수 있도록 세 개의 n*(m+n+1) 행렬 A, B, C를 구성합니다:

방정식 (3)은 방정식 (2)의 또 다른 표현입니다: 각 그룹 (ai, bi, ci)는 회로의 하나의 게이트에 해당합니다. 우리는 명시적으로 행렬 공식을 전개하기만 하면 됩니다:

따라서 LHS=RHS는 방정식 (2)와 완전히 동일하며, 행렬 방정식의 각 행은 하나의 1차 제약 조건(즉, 회로의 하나의 산술 게이트)에 해당합니다.

우리는 (A, B, C)를 구성하는 단계를 건너뛰었습니다. 사실 이 단계는 상대적으로 간단하고 직접적입니다. 우리는 해당 1차 제약 조건에 따라 행렬 형태로 변환하여 (A, B, C)의 각 행의 내용을 결정하기만 하면 됩니다. 첫 번째 행을 예로 들면: 첫 번째 1차 제약 조건 x와 x를 곱하여 s1이 성립하려면, 우리는 [0,1,0,0,0], [0,1,0,0,0] 및 [0,0,0,1,0,0]와 벡터 s를 곱해야 한다는 것을 쉽게 알 수 있습니다.

따라서 우리는 산술 게이트 회로를 행렬 공식으로 성공적으로 변환했습니다. 즉, 방정식 (3)입니다. 동시에 우리는 증명해야 할 객체를 증거 벡터 s로 전환했습니다.

3단계: 다항식

이제 z에 대한 다항식 집합을 정의하는 n*(n+m+1) 행렬 PA를 구성합시다:

이들은 여섯 개의 변수에 대한 네 개의 선형 방정식 집합으로, 전통적인 방법으로 해결할 수 있습니다. 그러나 이 경우 PA를 해결하는 더 효율적인 방법은 문제의 특성을 이용한 라그랑주 보간법입니다. 여기서는 PA를 해결하는 과정을 건너뛰겠습니다. 다소 번거롭지만 매우 직접적입니다.

여기서:

4단계: 타원 곡선 점

방정식 (4)를 다음과 같이 다시 씁니다:

여기서 i(z)=1은 z의 평범한 0차 다항식으로, 방정식을 통일하기 위해 사용됩니다 ------ 모든 항이 2차입니다. 이렇게 하는 필요성은 곧 명확해질 것입니다. 이 방정식은 z의 다항식의 덧셈과 곱셈만 포함하고 있습니다.

다음으로, 우리는 실제 작업 단계를 더 자세히 설명할 것입니다.

타원 곡선 암호화

타원 곡선의 일반 이론은 이 문서의 범위를 훨씬 초과합니다. 이 문서의 목적을 위해, 타원 곡선은 소수 체 Fp에서 E 함수로 매핑된 것으로 정의되며, 여기서 E는 y\^2=x\^3+ax+b를 만족하는 점(타원 곡선 점, 약칭 ECPs)을 포함합니다.

지금까지 우리는 일반 산술에 대해 논의해왔지만, 이제 소수 체로 전환할 때 숫자의 산술 연산은 모듈로 연산 방식으로 수행됩니다. 예를 들어 a+b=a+b(mod p), 여기서 p는 Fp의 차수입니다.

반면에, 두 개의 타원 곡선 점의 덧셈은 다음과 같이 정의됩니다:

구체적으로, 두 ECP P와 Q의 덧셈:

직선 PQ와 곡선 R의 교차점을 찾아 정의합니다 - (P+Q)로 정의됩니다.
곡선 R의 "거울" 점 R'로 반전합니다.
따라서 우리는 타원 곡선 점의 덧셈 P+Q=R'로 정의합니다:

이 규칙은 특별한 경우, 즉 ECP가 자기 자신을 더하는 경우에도 적용됩니다. 이 경우 해당 점의 접선을 사용합니다.

이제 우리가 임의로 점 G를 선택하고 숫자 1을 그 위에 매핑한다고 가정해 보겠습니다. (이러한 "초기 매핑"은 다소 임의적으로 들릴 수 있습니다. 나중에 논의할 것입니다.) 그런 다음 n이 Fp에 속하는 경우, 우리는 다음을 정의합니다:

E(N)=G+ G+ G+ …..+G=G 점 곱 n

이는 연산 표현식이 있습니다. +G의 연산을 "생성기"로 정의하고 g로 표기합니다. 그러므로 위의 정의는 다음과 같습니다:

타원 곡선에 익숙하지 않은 사람은 이 매핑을 일반적인 지수 함수에 비유할 수 있으며, 여기서 기수 g가 실수를 대체합니다. 산술 연산의 행동은 유사합니다. 그러나 중요한 차이점은 g\^n의 역함수가 계산적으로 불가능하다는 것입니다. 즉, 타원 곡선 버전의 을 계산할 방법이 없습니다. 이것이 바로 타원 곡선 암호화의 기초입니다. 이러한 매핑은 단방향 암호화라고 불립니다.

주목할 점은, 주어진 타원 곡선에서 G(따라서 "생성기" g의 선택)는 임의적이므로( x축의 점을 제외하고) 무한한 매핑 방식이 있다는 것입니다. (G 또는 g의 선택)은 지수 함수의 기수를 선택하는 것(2\^x, 10\^x, e\^x 등)과 유사하며, 이는 상식의 일부입니다.

그러나 앨리스가 증명하고자 하는 방정식 (5)는 이차 형태이므로 선형으로는 충분하지 않습니다. 이차 항을 처리하기 위해, 우리는 암호화된 공간에서 곱셈을 정의해야 합니다. 이것은 쌍 함수 또는 이중 선형 매핑이라고 하며, 다음에서 설명할 것입니다.

이중 선형 매핑

공개 참조 문자열

전체 과정은 "검증 키"라고 하며, 약칭 VK입니다. 여기서는 7개의 타원 곡선 점(ECPs)만 포함되며, 검증자에게 제공해야 합니다. 문제에 입력과 1차 제약 조건이 얼마나 포함되든 VK는 항상 7개의 ECPs로 구성됩니다.

또한 "신뢰할 수 있는 설정"과 특정 문제에 대한 PK 및 VK 생성 과정은 한 번만 수행하면 됩니다.

증명 및 검증

이제 공개 키(PK)를 가진 앨리스는 다음 타원 곡선 점(ECPs)을 계산합니다:

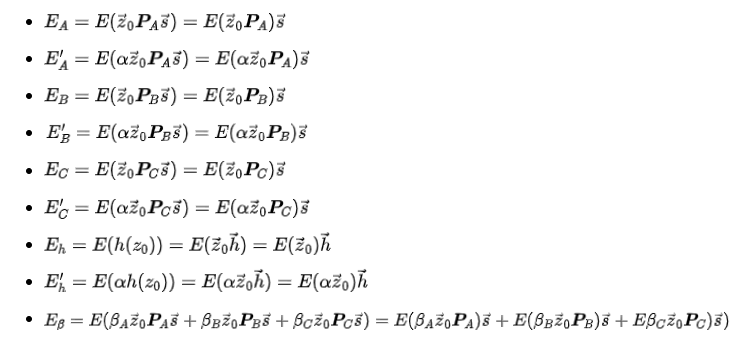
이 9개의 타원 곡선 점은 제로 지식 간결 비대화형 증명(zk-SNARK)의 핵심입니다!

주목할 점은, 앨리스가 실제로 공개 키의 타원 곡선 점에 대해 선형 조합 연산을 수행했다는 것입니다. 이 점은 특히 중요하며, 검증 시 주의 깊게 확인됩니다.

이제 앨리스는 zk-SNARK 증명을 제출했으며, 우리는 드디어 검증 단계에 들어갑니다. 세 단계로 진행됩니다.

먼저, 처음 8개의 타원 곡선 점이 실제로 일반 참조 문자열의 점들의 선형 조합인지 확인해야 합니다.

이 세 가지 검사가 모두 성립하면, 등식 (5)가 검증되며, 우리는 앨리스가 증거를 알고 있다고 믿습니다. 등식 뒤에 있는 이유를 설명해 보겠습니다. 첫 번째 부분의 첫 번째 등식을 예로 들면, 등식이 성립하는 이유는 이중 선형 성질 때문입니다: 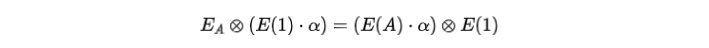그러나 앨리스는 기호 알파의 값을 모르기 때문에 이 덧셈을 명확히 계산할 수 없습니다. 그녀가 등식을 만족시키기 위해 생각해낼 수 있는 유일한 방법은 동일한 벡터 집합 s를 사용하여 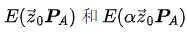의 두 조합을 계산하는 것입니다.

참고 문헌

"Zk-SNARKs: Under the Hood" (Vitalik Buterin)

"A Review of Zero Knowledge Proofs" (Thomas Chen, Abby Lu, Jern Kunpittaya, and Alan Luo)

"Why and How zk-SNARK Works: Definitive Explanation" (Maksym Petkus)

Website: Zero-Knowledge Proofs

Wikipedia: Elliptic curve

Wikipedia: Finite field

Wikipedia: Pairing-based cryptography