인터랙티브 증명을 비인터랙티브로 변환하는 방법은 무엇인가요?

저자: 강수跃, Fox Tech CEO; 맹현제, Fox Tech 수석 과학자

서론

암호학에서의 제로 지식 증명 기술은 web3 세계에서 광범위하게 사용되며, 개인 정보 계산, zkRollup 등 다양한 응용이 포함됩니다. 그 중 Layer2 프로젝트 FOX에서 사용하는 FOAKS는 제로 지식 증명 알고리즘입니다. 이러한 일련의 응용에서 제로 지식 증명 알고리즘에 있어 두 가지 속성이 매우 중요합니다. 바로 알고리즘의 효율성과 상호작용성입니다.

알고리즘 효율성의 중요성은 두말할 필요가 없습니다. 효율적인 알고리즘은 시스템 실행 시간을 현저히 줄여 클라이언트 지연을 감소시키고, 사용자 경험과 효율성을 크게 향상시킵니다. 이는 FOAKS가 선형 증명 시간을 실현하기 위해 노력하는 중요한 이유 중 하나입니다.

다른 한편으로, 암호학적 관점에서 제로 지식 증명 시스템의 설계는 종종 증명자와 검증자 간의 다중 상호작용에 의존합니다. 예를 들어, 많은 제로 지식 증명을 소개하는 대중 과학 기사에서 사용되는 "제로 지식 동굴" 이야기에서 증명의 구현은 알리바바(증명자)와 기자(검증자) 간의 다중 정보 전달 상호작용에 의존합니다. 그러나 실제로 많은 응용 시나리오에서 상호작용에 의존하면 시스템이 더 이상 사용 불가능해지거나 지연이 극도로 증가할 수 있습니다. zkRollup 시스템에서는 증명자(즉, FOX의 폴더)가 검증자와의 상호작용 없이 로컬에서 올바른 증명 값을 계산할 수 있기를 기대합니다.

이런 관점에서, 상호작용적인 제로 지식 증명 프로토콜을 비상호작용적으로 변형하는 방법은 매우 의미 있는 문제입니다. 이 글에서는 FOX가 고전적인 Fiat-Shamir 휴리스틱을 사용하여 Brakedown에서의 도전을 생성하여 비상호작용 프로토콜을 구현하는 과정을 소개하겠습니다.

제로 지식 증명에서의 Challenge

제로 지식 증명 알고리즘은 응용이 확산됨에 따라 매우 인기를 끌고 있으며, 최근 몇 년 동안 FOAKS, Orion, zk-stark 등을 포함한 다양한 알고리즘이 탄생했습니다. 이러한 알고리즘과 암호학계 초기의 시그마 프로토콜 등의 핵심 증명 논리는 증명자(Prover)가 먼저 특정 값을 검증자(Verifier)에게 전송하고, 검증자는 로컬에서 무작위 수를 생성하여 도전(Challenge)을 만들어 이 무작위로 생성된 도전 값을 증명자에게 전달해야 합니다. 증명자는 실제로 지식을 가지고 있어야만 높은 확률로 검증자의 응답을 할 수 있습니다. 예를 들어 제로 지식 동굴에서 기자가 동전을 던져 알리바바에게 왼쪽에서 나올지 오른쪽에서 나올지를 알려주는 경우, 여기서 "왼쪽과 오른쪽"은 알리바바에 대한 도전입니다. 만약 그가 정말로 주문을 알고 있다면 반드시 요구된 방향으로 나올 수 있지만, 그렇지 않으면 반의 확률로 실패하게 됩니다.

여기서 우리는 Challenge의 생성이 매우 중요한 단계임을 주목해야 합니다. 이는 두 가지 요구 사항이 있습니다: 무작위성과 증명자가 예측할 수 없는 것입니다. 첫 번째, 무작위성은 그 확률 속성을 보장합니다. 두 번째, 만약 증명자가 도전 값을 예측할 수 있다면 이는 프로토콜의 안전성이 파괴된다는 것을 의미합니다. 증명자가 지식이 없어도 검증을 통과할 수 있습니다. 예를 들어, 알리바바가 기자가 그에게 어느 쪽에서 나올지를 예측할 수 있다면, 그는 주문이 없어도 미리 그 쪽으로 들어갈 수 있으며, 결과적으로 프로토콜을 통과할 수 있습니다.

따라서 우리는 증명자가 스스로 로컬에서 이러한 예측할 수 없는 무작위 수를 생성할 수 있도록 하면서도 검증자가 검증할 수 있는 방법이 필요합니다. 이렇게 하면 비상호작용 프로토콜을 구현할 수 있습니다.

해시 함수 (Hash Function)

해시 함수라는 이름은 우리에게 낯설지 않을 것입니다. 비트코인의 합의 프로토콜 POW에서 채굴의 수학적 문제를 수행하든, 데이터 양을 압축하든, 메시지 인증 코드를 구성하든 해시 함수의 흔적이 있습니다. 위의 다양한 프로토콜에서 사실 해시 함수의 다양한 속성이 활용되고 있습니다.

구체적으로, 안전한 해시 함수의 속성은 다음과 같습니다:

압축성: 결정적인 해시 함수는 임의 길이의 메시지를 고정 길이로 압축할 수 있습니다.

유효성: 주어진 입력 x에 대해 출력 h(x)를 계산하는 것은 쉽습니다.

충돌 저항성: 주어진 입력 x1에 대해 다른 입력 x2를 찾아 h(x1) = h(x2)가 되도록 하는 것은 어렵습니다.

주의할 점은, 해시 함수가 충돌 저항성을 만족한다면 반드시 단방향성을 만족해야 한다는 것입니다. 즉, 주어진 출력 y에 대해 h(x) = y를 만족하는 x를 찾는 것은 어렵습니다. 암호학에서는 이론적으로 절대적으로 단방향성을 만족하는 함수를 구성할 수는 없지만, 해시 함수는 실제 응용에서 기본적으로 단방향 함수로 간주될 수 있습니다.

이렇게 보면, 위의 몇 가지 응용은 각각 해시 함수의 몇 가지 다른 속성과 대응되며, 해시 함수는 무작위성을 제공하는 중요한 역할도 합니다. 비록 암호학 이론에서 요구하는 완벽한 무작위 수 생성기는 현재로서는 구성할 수 없지만, 해시 함수는 실제로 이 역할을 수행할 수 있습니다. 이는 후속에서 소개할 Fiat-Shamir 휴리스틱의 기술을 위한 기초를 제공합니다.

Fiat-Shamir 휴리스틱 (Heuristic)

사실, Fiat-Shamir 휴리스틱은 해시 함수를 이용하여 앞서 생성된 스크립트에 대해 해시 연산을 수행하여 값을 얻고, 이 값을 도전 값으로 사용하는 것입니다.

해시 함수 H를 무작위 함수로 간주하면, 도전은 균일하게 무작위로 선택되며, 증명자의 공개 정보와 약속과 독립적입니다. 안전성 분석에 따르면 앨리스는 H의 출력을 예측할 수 없으며, 이를 오라클로 간주해야 합니다. 이러한 경우, 앨리스가 프로토콜을 따르지 않고도 올바른 응답을 할 확률(특히 필요한 비밀을 모를 때)은 H의 값의 범위의 크기에 반비례합니다.

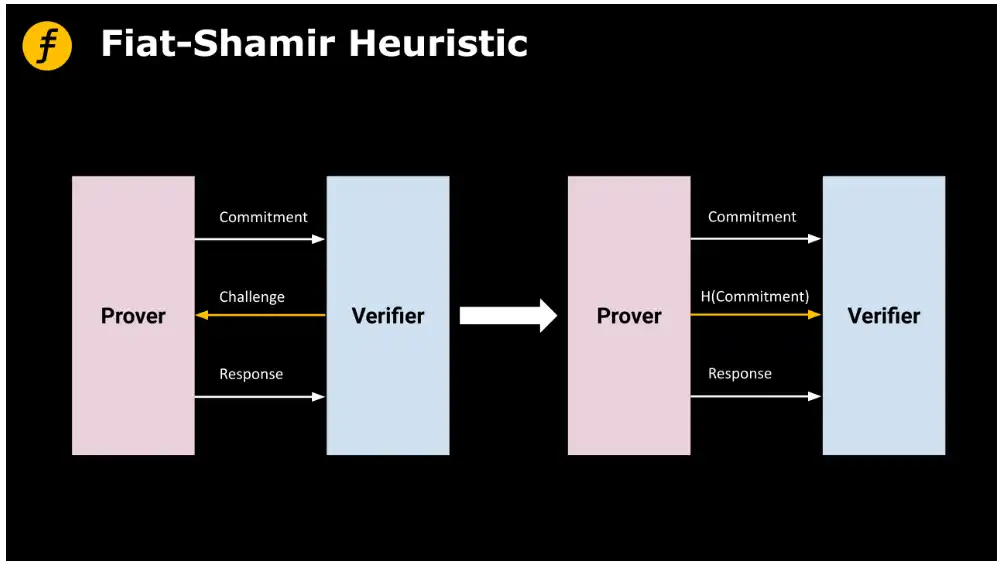
그림 1: Fiat-Shamir 휴리스틱을 이용한 비상호작용 증명 비상호작용 FOAKS

이 섹션에서는 FOAKS 프로토콜에서 Fiat-Shamir 휴리스틱의 적용을 구체적으로 보여주며, 주로 Brakedown 부분의 도전을 생성하여 비상호작용 FOAKS를 구현하는 데 사용됩니다.

먼저 Brakedown에서 증명을 생성하는 단계에서 도전이 필요한 단계는 "근접성 검증" 및 Merkle Tree의 증명 부분입니다(독자는 이전의 글 "FOAKS에서의 다항식 약속 프로토콜 Brakedown 이해하기"를 참조할 수 있습니다). 첫 번째 점에서 원래의 과정은 증명자가 검증자가 생성한 무작위 벡터를 검증해야 하는 것입니다. 계산 과정은 아래 그림과 같습니다:

그림 2: 비상호작용 증명 FOAKS에서의 Brakedown Checks

이제 우리는 해시 함수를 사용하여 증명자가 스스로 이 무작위 벡터를 생성하도록 합니다.

0=H(C1,R, r0,r1)로 설정하고, 검증자의 검증 계산에서도 이 0을 계산하는 단계를 추가해야 합니다. 이러한 구성에 따라, 증명자는 도전 값을 미리 예측할 수 없으므로 미리 도전 값에 따라 "부정행위"를 할 수 없으며, 즉 가짜 약속 값을 생성할 수 없습니다. 또한 해시 함수 출력의 무작위성에 따라 이 도전 값도 무작위성을 만족합니다.

두 번째 점에 대해, I=H(C1,R, r0,r1,c1,y1,c0,y0)로 설정합니다.

우리는 의사 코드를 사용하여 변형된 비상호작용 Brakedown 다항식 약속에서의 증명 및 검증 함수를 제시합니다. 이는 FOAKS 시스템에서 사용되는 함수입니다.

function PC. Commit()：

w를 kk 행렬로 파싱합니다. 증명자는 로컬에서 텐서 코드 인코딩 C1, C2를 계산합니다. C1은 kn 행렬이고, C2는 nn 행렬입니다.

for i [n] do

Merkle 트리 루트 Roott=Merkle.Commit(C2[:,i])를 계산합니다.

Merkle 트리 루트 R=Merkle.Commit([Root0,……Rootn-1])를 계산하고, R을 약속으로 출력합니다.

function PC. Prover(, X, R)

증명자는 0Fk라는 무작위 벡터를 생성합니다: 0=H(C1,R, r0,r1)

근접성: c0=i=0k-10[i]C1[:,i],y0=i=0k-10[i]w[i]

일관성: c1=i=0k-1r0[i]C1[:,i],y1=i=0k-1r0[i]w[i]

증명자는 c1,y1,c0,y0를 검증자에게 보냅니다.

증명자는 I라는 벡터를 도전으로 계산합니다. 여기서 I=H(C1,R, r0,r1,c1,y1,c0,y0)입니다.

for idxI do

증명자는 C1 [:,idx]와 R 하의 C2 [:,idx]에 대한 Merkle 트리 증명을 검증자에게 보냅니다.

function PC. VERIFY_EVAL(X,X,y=(X),R)

근접성: idxI,C0[idx]==\<0,C1[:,idx]> 및 EC(y0)==C0

일관성: idxI,C1[idx]==\<r0,C1[:,idx]> 및 EC(y1)==C1

y==\<r1, y1>

idxI, EC(C1[:,idx])는 ROOTidx와 일치하며, ROOTidx의 Merkle 트리 증명이 유효합니다.

모든 조건이 충족되면 수락을 출력합니다. 그렇지 않으면 거부를 출력합니다.

결론

많은 제로 지식 증명 알고리즘은 설계 초기부터 증명자와 검증자 간의 상호작용에 의존하지만, 이러한 상호작용 증명 프로토콜은 효율성을 추구하고 네트워크 통신 비용이 큰 응용 시나리오에서는 적합하지 않습니다. 예를 들어, 체인 상 데이터 개인 정보 보호 및 zkRollup 등에서 그렇습니다. Fiat-Shamir 휴리스틱을 통해 증명자는 프로토콜의 안전성을 해치지 않으면서 로컬에서 무작위 수 "도전"을 생성할 수 있으며, 이는 증명자가 검증할 수 있습니다. 이러한 방법에 따라 FOAKS는 비상호작용 증명을 구현하고 시스템에 적용하였습니다.