5분 만에 알아보는 AMM 기반 무청산 대출 프로토콜 Timeswap

撰文：iambabywhale.eth，ForesightNews

현재 시장에서 새로운 퍼블릭 체인의 출시는 거의 두 가지 DeFi 프로토콜의 구축과 함께 이루어집니다. 하나는 AMM 기반의 DEX이고, 다른 하나는 대출입니다. 두 가지 모두 필요한 유동성은 새로운 퍼블릭 체인이 초기 자본을 축적하는 데 기여하며, 이후 경제 인프라 구축을 촉진합니다. 이 중 DEX는 대부분 연합 곡선을 이용해 거래를 처리하며, 간단한 수학 모델 덕분에 DEX의 논리에서 결함이 발생할 가능성이 적습니다. 그러나 이웃의 대출 프로토콜은 오라클과 같은 복잡한 구성 요소로 인해 공격 위험이 존재합니다.

그렇다면 연합 곡선을 이용해 대출 시장을 구축할 수 있을까요? Polygon의 Timeswap이 해결책을 제시했습니다.

프로토콜 소개

Timeswap은 Polygon 위에 구축된 AMM 기반의 무청산 대출 프로토콜입니다. 프로토콜의 메커니즘은 나중에 자세히 설명하겠지만, 먼저 Timeswap의 기본 정보를 살펴보겠습니다.

Timeswap은 2022년 3월 22일 메인넷에 출시되었으며, 현재 팀은 프로토콜 테스트를 위해 가끔 작은 대출 시장을 열고 있습니다. 사용자는 Polygon에서 자신의 USDC를 대출하거나 MATIC을 담보로 USDC를 빌릴 수 있습니다. Timeswap은 2021년 10월에 시드 라운드 자금을 완료했다고 발표했지만, 자금 조달 금액은 공개하지 않았습니다. 이 라운드에 참여한 투자자는 Multicoin Capital, Mechanism Capital 및 Defiance Capital이 포함됩니다.

Timeswap의 창립 팀은 주로 필리핀인으로 구성되어 있으며, 창립자 Ricsson Ngo는 필리핀 마닐라 아테네오 대학교에서 금융 수학 석사 과정을 마쳤고, 필리핀 지역 커뮤니티 교육 플랫폼 Einstar의 창립자이기도 합니다. 공동 창립자 Harshita Singh는 이전에 인도의 월마트에서 공급망 관리자로 일했습니다. 또 다른 공동 창립자 Ameeth Devadas는 프로젝트와 자본을 연결하는 투자 플랫폼의 제품 관리자였으며, 더 중요한 것은 그가 Polygon의 엔젤 투자자라는 점입니다. 창립 팀의 다른 멤버로는 Zapper.fi의 창립자 Dipesh Sukhani, 전 Polygon 재무 부사장 Keyur Shah 등이 있습니다.

실현 메커니즘

현재 대출 프로토콜의 모델은 대부분 유동성 제공자가 대출 풀을 제공하고, 대출자는 초과 담보로 다른 토큰을 담보로 하여 풀에서 대출을 받으며, 유동성 제공자는 대출자의 이자 수익을 얻는 구조입니다. 담보의 가치가 특정 임계값 이하로 떨어지면 담보를 매각하여 청산하고, 일부는 LP의 손실을 보상하고 일부는 청산자의 이익이 됩니다.

Timeswap은 연합 곡선을 통해 자동화된 대출을 실현하며, 오라클 가격 제공이 필요 없고 담보 청산도 발생하지 않습니다. 앞서 언급한 대출 프로토콜 모델에서는 특정 자산에 대한 가격 제공을 위한 오라클이 조작되어 프로토콜이 공격받는 사건이 발생했습니다. Timeswap은 연합 곡선을 통해 오라클 공격이 발생하지 않으며 허가 없이 개방된 대출 시장을 구축하고, 궁극적으로 대규모 화폐 시장으로 성장하기를 희망합니다.

현재 대출 프로토콜의 함수는 XYZ=k입니다. 여기서 X는 원금 토큰 수, Y는 초당 수익, Z는 담보 토큰 수를 나타내며, k는 상수로 Uniswap의 XY=k 모델과 유사합니다.

예를 들어, 제가 6개월 동안 DAI-ETH 대출 풀을 설정하고, 초기 자본이 10,000 DAI, 기대하는 초기 연간 수익률이 15%이며 담보 비율이 167%일 때, 이때 X=10000이고 연간 수익률 15%는 초당 수익 Y가 0.0000475 DAI임을 의미합니다. 이때 이더리움 가격이 4000 DAI라고 가정하면 Z는 10000*1.67/4000=4.175가 되므로 초기 곡선 공식은 다음과 같습니다:

XYZ=10000*0.0000475*4.175=1.98=k

풀 설정이 완료되면 시장에는 세 가지 유형의 사용자가 나타납니다. 각각 유동성을 계속 추가하고자 하는 LP, 대출자 및 차입자입니다. 원리는 Uniswap의 유동성 제공자와 거래자와 유사합니다. 유동성을 추가하거나 철회할 때 매개변수는 비례적으로 증가하거나 감소하며, k 값이 변경됩니다. 시장에 새로운 대출자나 차입자가 추가되거나 퇴출될 때 매개변수는 X와 Z의 증가 및 감소에 따라 자동으로 조정됩니다.

Timeswap은 모든 참여자에게 서로 다른 풀의 지분을 나타내는 ERC-20 및 ERC-721 토큰을 발급하고, 시장이 종료된 후 실제 풀에 남아 있는 자금을 비례적으로 분배하여 이를 실현합니다.

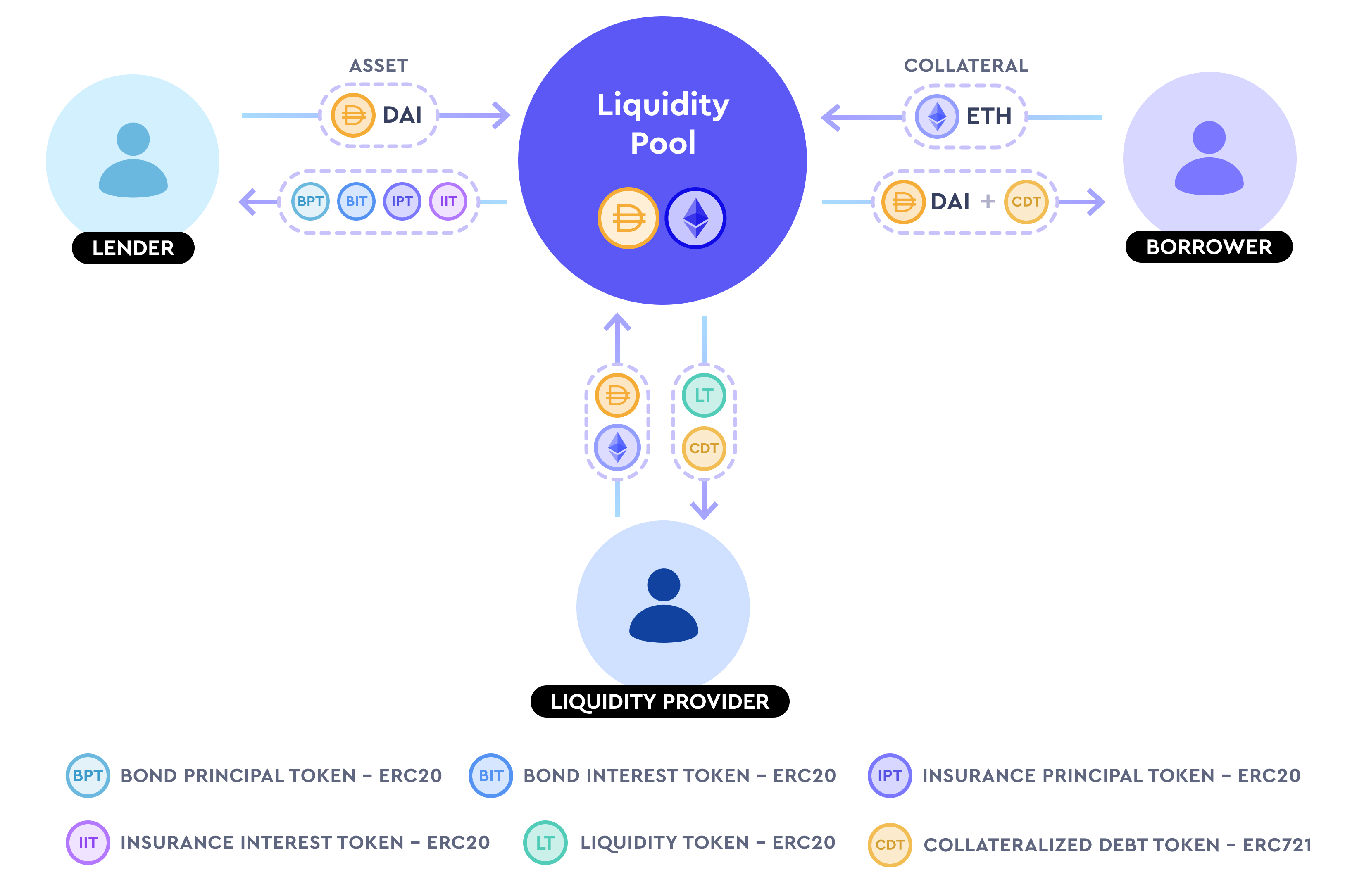
대출자

대출자는 프로토콜에 대출 가능한 자산을 추가하는 사용자입니다. 이 사용자는 대출 가능한 자산을 전송한 후 4종의 토큰을 받습니다: 채권 원금 토큰(BPT), 채권 이자 토큰(BIT), 보험 원금 토큰(IPT), 보험 이자 토큰(IIT).

여기서 BPT는 대출 자금 풀의 지분을 나타내며, 이 자금 풀은 초기 대출 자산과 대출자가 입금한 자금을 빼고 차입자가 대출한 자금의 총액입니다. BIT는 이자 풀의 지분으로, 차입자가 지불한 모든 이자의 풀입니다. IPT는 대출자의 채권 토큰 중 실현되지 않은 자산이 대출자가 보유한 보험 범위 내의 지분을 나타냅니다. IIT는 채권 이자 토큰의 미실현 자산의 지분을 나타냅니다.

차입자

차입자는 담보 자산을 입금하여 자금을 대출받고, ERC-721 형식의 담보 채무 토큰(CDT)을 받습니다. 이 토큰은 차입자가 지불해야 할 이자와 잠금된 담보에 대한 정보를 기록합니다. 만기 전에 차입자가 채무를 상환하면 해당 토큰은 소각되고 담보는 해제됩니다. 그렇지 않으면 담보는 대출자에게 분배됩니다.

유동성 제공자

유동성 제공자는 유동성을 제공한 후 LP 토큰을 받고, 대출자와 차입자 간의 이자 차이를 통해 수익을 얻습니다. 공식 문서에 명시된 유동성 제공자가 받는 CDT 토큰은 수익의 지분을 나타낼 수 있으며, 단순히 오류일 수도 있습니다.

대출 행동 발생 시 데이터 변화

대출 행동이 발생하거나 유동성이 증가 또는 감소할 때, 유동성 제공자가 차지하는 지분의 변화는 계산하기 어렵지 않습니다. 왜냐하면 그들은 LP 토큰만 받기 때문입니다. 이 중에서 가장 복잡한 계산은 대출자와 차입자입니다. 공식 문서의 데이터를 예로 들어보겠습니다.

여기서 미리 설명해야 할 점은, 사용자가 대출 또는 차입을 선택할 때 수익률과 담보 자산 간의 관계를 스스로 선택할 수 있다는 것입니다. 예를 들어 대출자는 수익률을 낮추어 자신이 대출한 자산이 차입자의 담보 자산으로 커버되는 비율을 높일 수 있습니다. 차입자도 담보 자산의 수량을 늘려 대출 이자를 낮출 수 있습니다. 그러나 그럼에도 불구하고 차입자에게 미치는 영향은 크지 않습니다. 왜냐하면 차입자는 거래 시의 데이터에 따라 이자를 지불하면 되기 때문입니다.

대출자

이제 DAI/ETH 대출 풀의 초기 매개변수가 X=10000, Y=0.0000475(연간 이자율 15%), Z=4.16, k=1.979이고, 기간이 1년이라고 가정해 보겠습니다. 이때 A가 해당 풀의 기간 종료 한 달 전에 1000 DAI를 입금하고 10%의 연간 수익률을 선택했다고 가정합니다. 이때 x=1000이며, A의 최대 수익률은 z=0일 때, 즉 수익을 전혀 보장하지 않는 경우 y=0.00000425가 되며, 최대 수익은 약 13.41%입니다. Timeswap은 최소 수익률을 최대 수익의 1/16으로 정의하며, 여기서는 0.84%로 대출자가 어느 정도 수익을 보장받을 수 있도록 합니다.

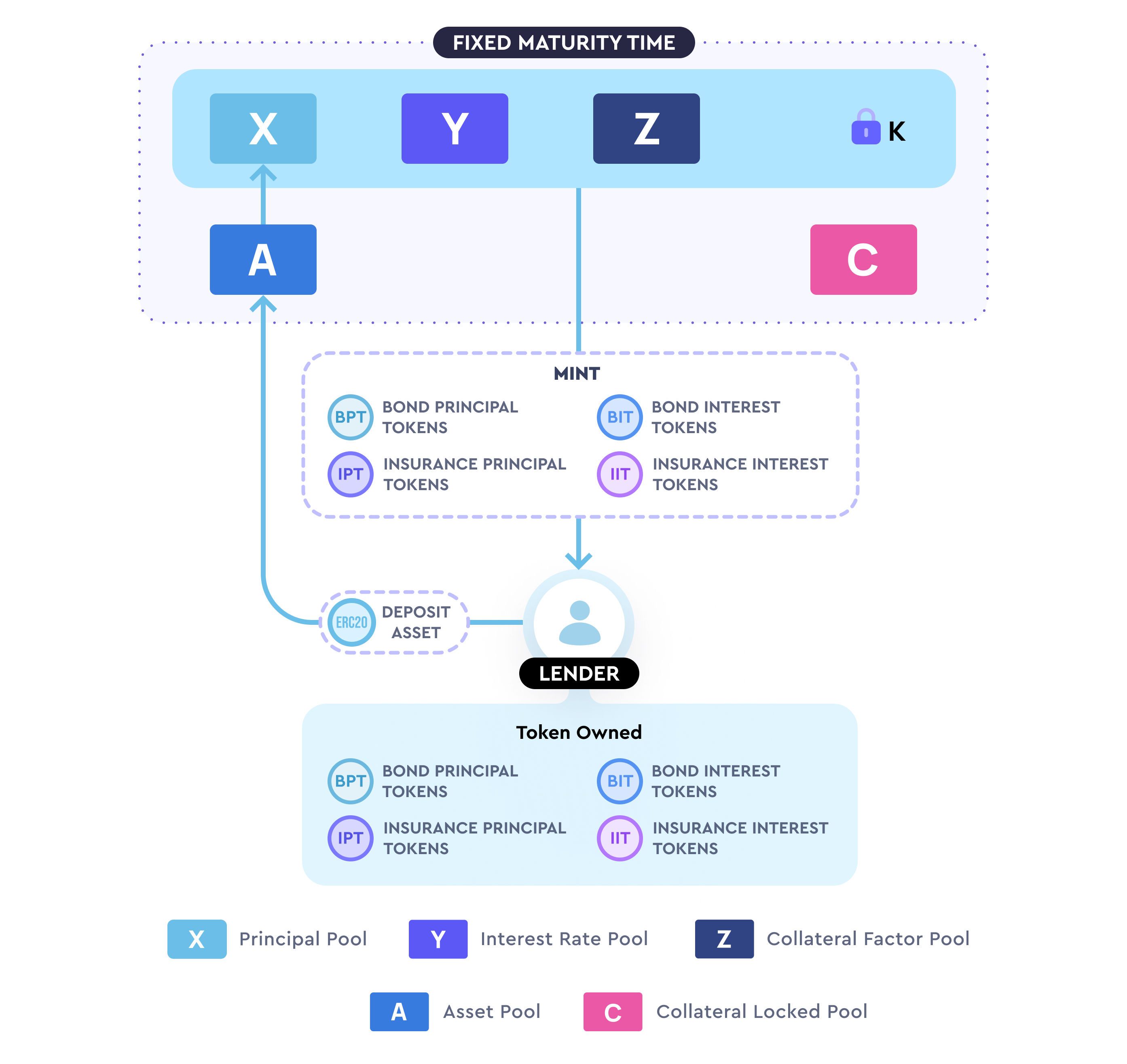
A의 원금은 1000 DAI이므로 1000 BPT 토큰을 받게 됩니다. 10%의 연간 수익률로 30일 동안 보관하면 약 8.19 DAI를 받게 되므로 8.19 BIT 토큰을 받게 됩니다.

다음으로 IPT와 IIT 토큰의 수량을 계산합니다. A가 받을 IPT 수량은 Y가 변하지 않을 때 Z의 변화량으로, 본 예에서는 0.37입니다. 즉 A는 0.37 IPT 토큰을 받게 됩니다. 이제 10%의 수익률을 계산에 대입하면 Z의 변화량 z는 0.1이 되며, IIT의 계산 방식은 z*30일의 초 수 / 2\^25=0.0077입니다. 즉 A는 0.0077 IIT 토큰을 받게 됩니다.

최종 정산 시 원금과 수익 중 어느 한 쪽이라도 부족할 경우 해당 보험 토큰을 사용하여 상환합니다. 만약 DAI 풀의 토큰이 대출자에게 상환하기에 충분하다면 이더리움 토큰 풀을 사용할 필요가 없습니다.

차입자

대출자를 예로 들었으니 차입자의 계산도 자연스럽게 이어집니다. X의 변화로 인해 Y와 Z의 변화가 발생하는 것이 아니라, Z의 변화로 인해 X와 Y의 변화가 발생하는 것입니다.

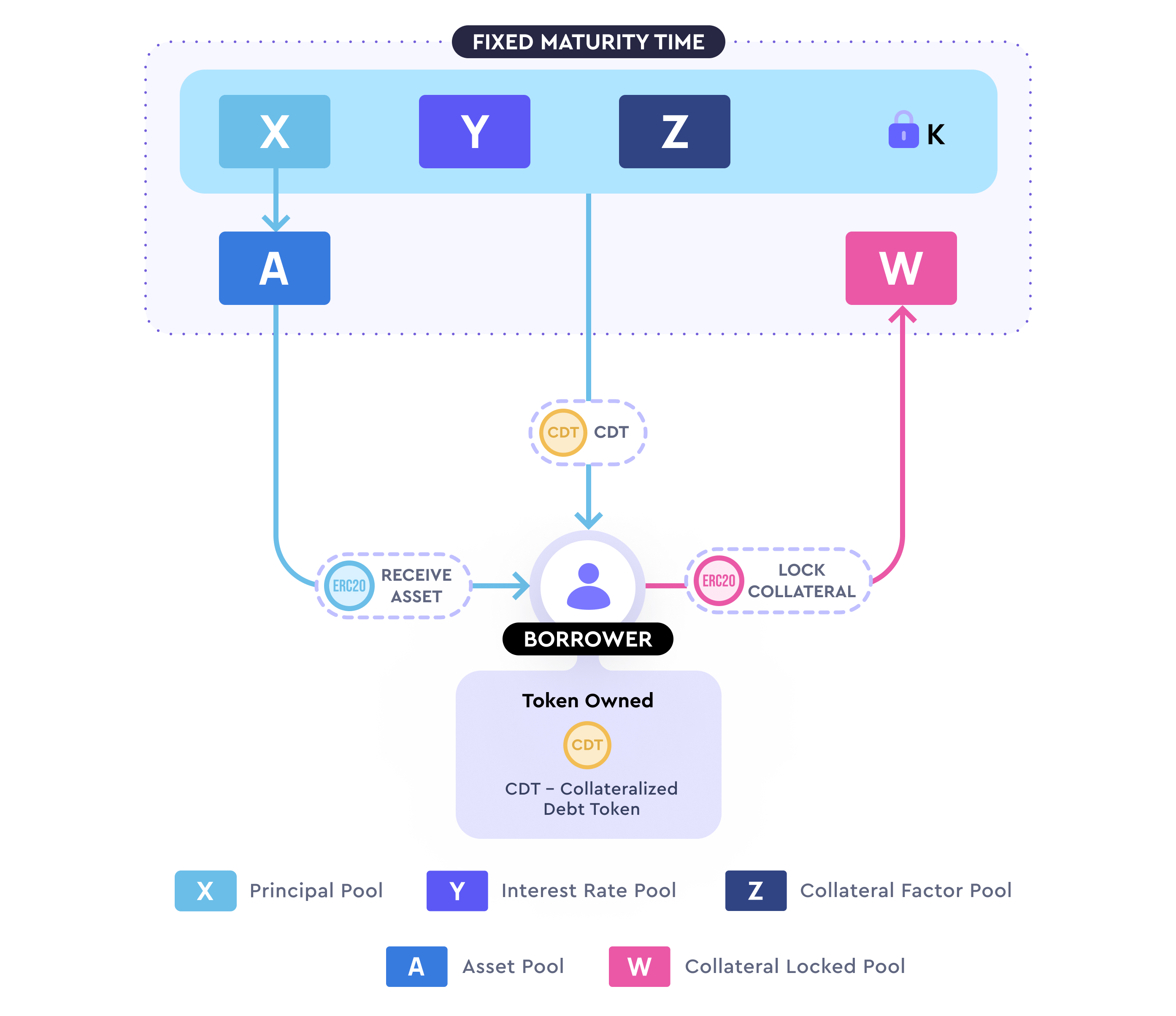
이때 B가 같은 시간, 같은 대출 풀에서 10%의 이율로 1000 DAI를 대출받고자 한다고 가정합니다. 동일한 계산 방법에 따라 B는 최종적으로 1008.19 DAI를 상환해야 담보 자산을 회수할 수 있으며, 담보 자산의 계산이 핵심입니다. 먼저 최소 담보 수량을 계산합니다. 즉 Y가 변하지 않을 때 X가 1000 감소하면 Z의 변화량은 0.469가 됩니다. 이후 10%의 이율로 z의 변화량을 계산하면 0.18이 되며, 0.18*30일의 초 수 / 2\^25=0.139가 됩니다. 따라서 B는 총 0.4829 ETH를 담보로 제공해야 DAI를 대출받을 수 있으며, 담보 비율은 190%를 초과합니다.

요약

Timeswap은 세 가지 가변 매개변수를 사용하여 대출 풀의 데이터를 실시간으로 처리합니다. 이러한 솔루션의 장점은 오라클 가격 제공 문제로 인해 공격받지 않으며, 긴 꼬리 자산도 Timeswap에서 자유롭게 시장을 설정할 수 있다는 점입니다. 그러나 분산화된 시장으로서 Timeswap도 몇 가지 문제를 안고 있습니다. 예를 들어 Aave의 대출 시장에서는 대출자로서 손실이 거의 발생하지 않을 가능성이 높습니다. 왜냐하면 담보 자산이 일정 수준 이하로 떨어지면 청산되어 대출자가 투자한 자금을 보상하기 때문입니다. Timeswap은 현재 정기적인 대출 시장으로, 만기 시 시장이 크게 변동하여 담보 자산 가격이 대출 자산 가격보다 낮아지면 대출자는 담보 자산을 보상으로 받았지만 여전히 법정 화폐 기준으로 손실이 발생할 수 있습니다.

또한 Timeswap이 원금과 수익 토큰을 분리한 이유는 이전 테스트에서 두 가지를 구분하지 않았기 때문입니다. 즉 대출자가 원금 비율에 따라 최종 자금 풀을 분배하게 되면, 특정 APR이 짧은 시간 내에 극도로 높아지는 경우 대출자가 대량의 원금 토큰을 받을 수 있어 최종적으로 풀에서 대부분의 토큰을 가져가게 되어 일부 초기 대출자는 원금 손실을 겪을 수 있습니다. 따라서 두 가지 토큰을 설정함으로써 대출자의 원금 안전을 최대한 보장하고, 보험도 원금과 수익이 분리된 상태에서 보장됩니다.

Timeswap은 흥미로운 시도를 했으며, 앞으로 현재의 대출 플랫폼을 기반으로 제품을 점차 풍부하게 하여 대규모 분산화 화폐 시장을 구축할 것입니다.