なぜ「全同態暗号 FHE」は暗号スキームの聖杯なのか？

原文タイトル： 《完全同態暗号 (FHE)》
著者：Evan Fisher & Vikramaditya Singh ，Portal Ventures
編纂：深潮TechFlow
FHEは計算の聖杯であり、価値と計算はオープンで許可不要のネットワークに移行しており、FHEは必要なインフラとアプリケーションの大部分を支えるでしょう。

市場が熊市の静寂に包まれる中、投資家やプロジェクト側は常に新しい成長ポイントを探し始めます。

持続的なホットトピックが欠如している空白期間は、新技術を探求し深く理解する絶好の機会です。なぜなら、新技術は次の市場の物語の中心になる可能性があるからです。

先月、有名な暗号ベンチャー企業Portal Venturesは、その公式ブログで完全同態暗号（FHE）技術を詳細に探討した記事を発表しました。しかし、この深い技術的記事は、一般の人々の広範な関心を引くことはなかったようです。

Portal Venturesの著者はこう述べています："完全同態暗号は暗号スキームの聖杯です"。

VCが注目する技術を理解することは、投資家にとって非常に重要です。なぜなら、それは次の市場サイクルの潜在的なトレンドを予測し理解するのに役立つからです。実際、同態暗号、ゼロ知識証明、マルチパーティ計算などの技術は、暗号学の分野で深遠な影響を持ち、特に完全同態暗号は暗号通貨やWeb3の分野で巨大な応用可能性を持つかもしれません。

しかし問題は、大多数の人々が完全同態暗号の真の意味、どのように機能するのか、他の技術との違いについてほとんど知らないということです。市場が不景気で投資感情が低迷している時に、炒作の喧騒から抜け出し、これらの最前線技術を深く研究し理解することは、間違いなく賢明な選択です。

偶然にも、筆者は数年前に仕事でFHEに関連する技術ソリューションに触れる機会がありました。そこで、Portal Venturesのこの記事を深く解読し、皆さんに新しい視点と考察を提供したいと思います。

同態と完全同態暗号、いったい何なのか？

Portal Venturesの原文を直接見ると、完全同態暗号（FHE）の複雑な数学的記述に困惑するかもしれません。

実際、暗号学の世界は奥深く技術的ですが、私たちはこれらの概念をシンプルで分かりやすい方法で説明することができます。このセクションでは、筆者がより直感的で理解しやすい例を提供し、完全同態暗号を深く理解する手助けをしようとしています。

まず、「秘密の魔法の箱」を想像してください。あなたはこの箱に任意の物を入れ、ロックすることができます。一度ロックすると、箱の中身を見ることも触れることもできません。しかし驚くべきことに、この魔法の箱は、開けることなく中の物の色や形を変えることを許可します。

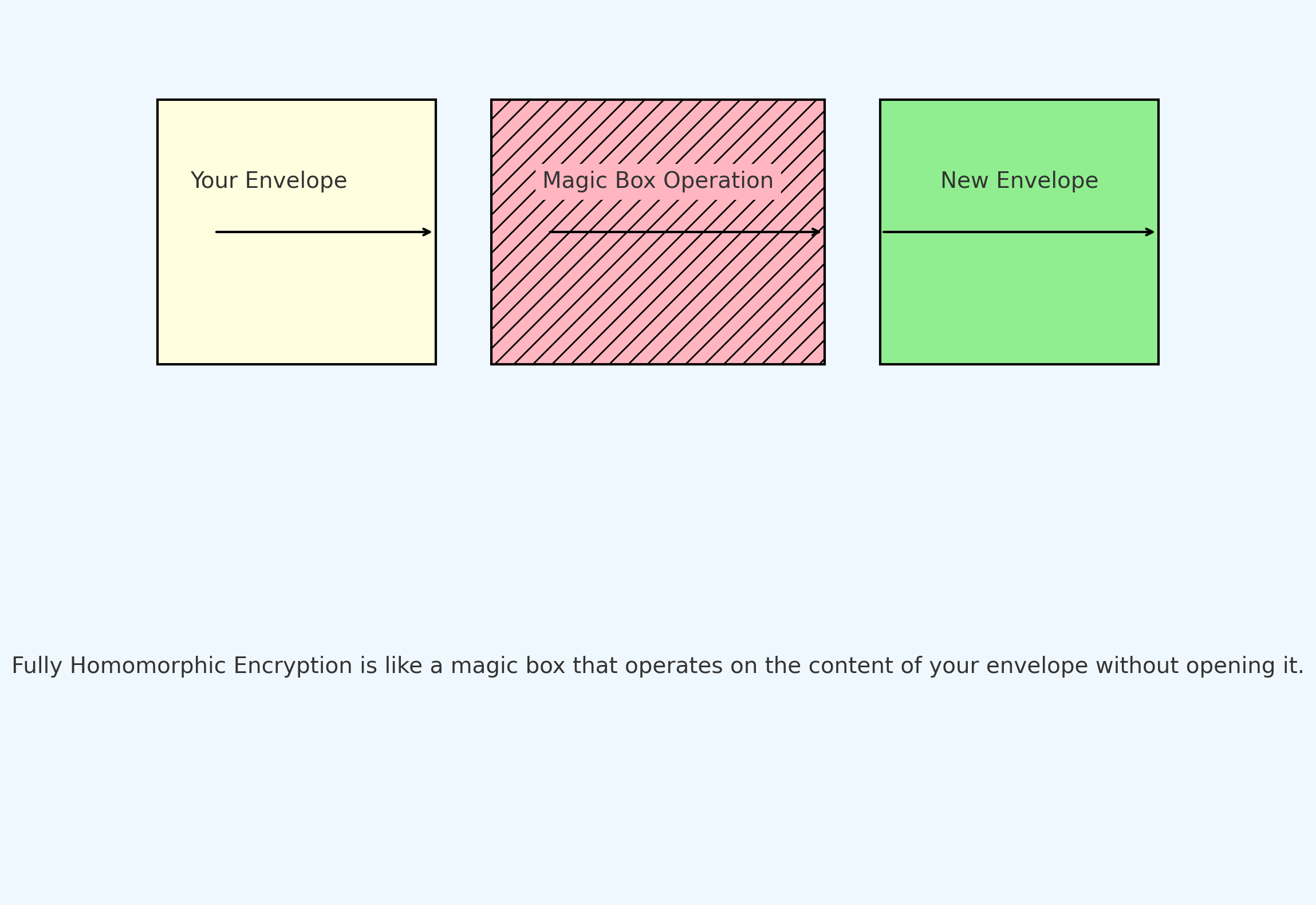
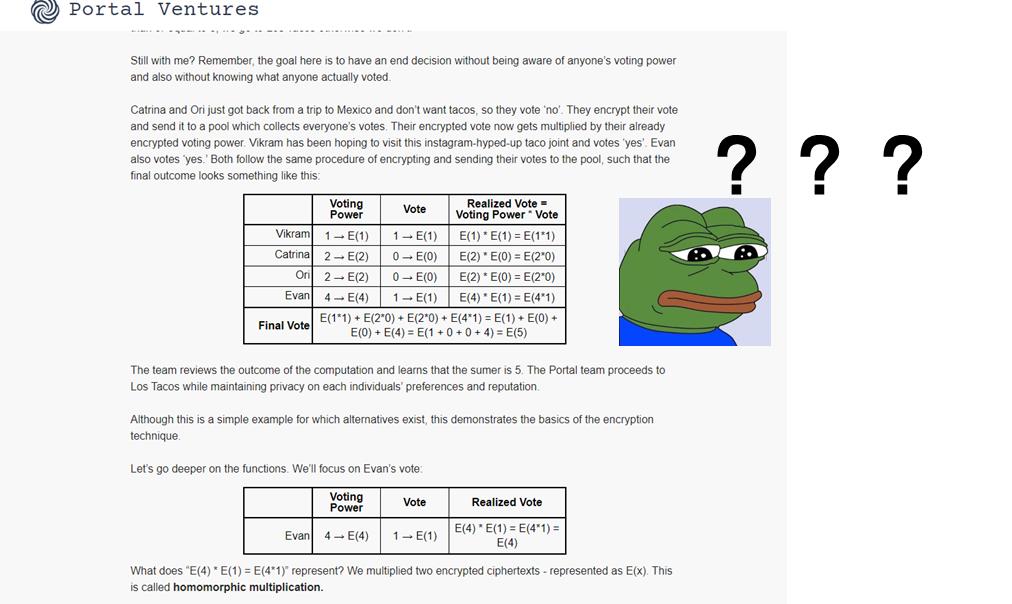
上の図のように、完全同態暗号（Fully Homomorphic Encryption）は魔法の箱として見ることができます：

1. あなたの封筒 (Your Envelope): これはあなたが暗号化したい元データを表します。

2. 魔法の箱操作 (Magic Box Operation): 解読したり封筒を開けたりすることなく、封筒内のデータに対して操作（加算、減算などの計算）を行うことができます。

3. 新しい封筒 (New Envelope): 魔法の箱操作を経て、新しい暗号化結果を得ることができます。

これが同態暗号の基本的な考え方です：データ自体を理解することなく、暗号化されたデータに対して操作を行うことができる。

この分かりやすい例は、「完全同態暗号」が何をしているのかを明確にするのに役立ちます。しかし実際には、この概念自体は少し難解です。それでは、「完全」と「同態」とは何でしょうか？

1. 「完全」（Fully）とは何か？

• 暗号学において、暗号スキームは加算、乗算などの多様な操作をサポートできます。私たちがある暗号スキームが「完全同態」であると言うとき、それはその暗号スキームが暗号化されたデータ上で任意の数の基本的な演算（例えば加算と乗算）を行うことをサポートすることを意味します。これは部分同態暗号（加算のみまたは乗算のみをサポートするスキーム）とは対照的です。

1. 「同態」（Homomorphic）とは何か？

• 「同態」はギリシャ語に由来し、「同じ形または構造」を意味します。暗号学において、暗号スキームが同態であると言うとき、それは明文上の効果と暗号文上の効果が同じであることを意味します。言い換えれば、暗号化されたデータに対してある操作を行い、その結果を解読すると、データを先に解読してから同じ操作を行うのと同等です。

1. 例えば、同態加算をサポートする暗号スキームを考えてみましょう。あなたが3と4という2つの数字を持っていると仮定します。まずこれらの数字を暗号化し、その後この同態暗号スキームを使用して2つの暗号化された数字を加算します。最後に、加算された結果を解読します。得られる解読結果は7となり、これは明文の3と4を直接加算した結果と同じです。

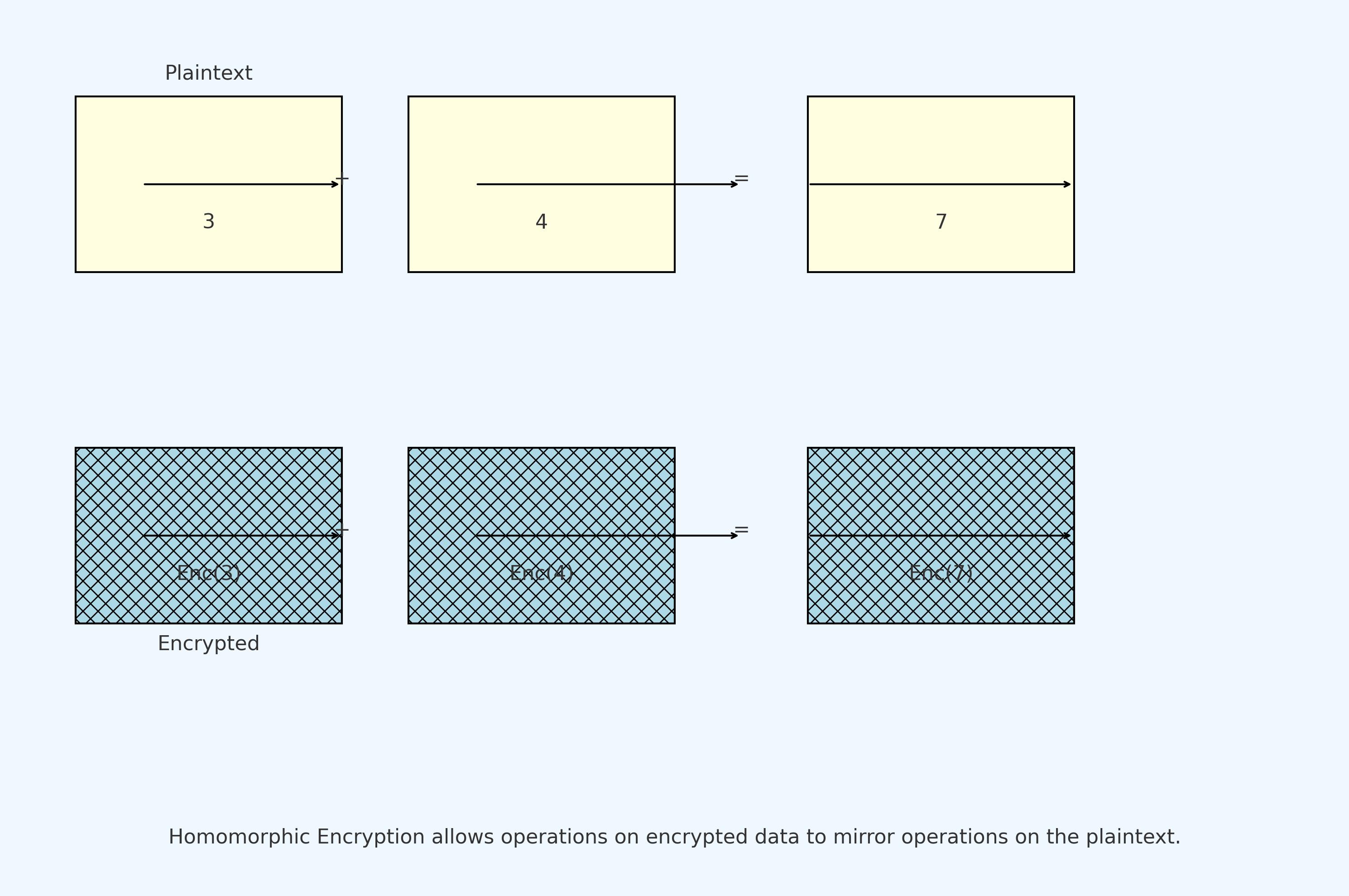
しかし、あなたはどうやって非数字に対してこれらの加減乗除を行うのかと疑問に思うかもしれません。実際には、特定のエンコーディング方法を使用して非数字データを数字形式に変換し、それに対して加算や乗算などの演算を行うことができます。これは、完全同態暗号の応用が数学的計算に限らず、他の分野にも広く適用できることを意味します。

この概念をより直感的に説明するために、医療データの例を考えてみましょう。

1. 病院には患者のデータがあり、年齢や血糖値などがありますが、プライバシーの観点から直接クラウドサービスプロバイダーに送信して分析したくないとします。

2. 完全同態暗号を使用することで、病院はこれらのデータをまず暗号化できます。

3. クラウドサービスプロバイダーは、すべての患者の平均年齢（加算と除算が必要）と血糖値の合計と患者数の積（加算と乗算が関与）を計算する必要があります。

4. これらすべての計算は、データを解読することなく暗号化されたデータ上で行うことができます。クラウドサービスプロバイダーはデータを解読することなく計算を完了し、暗号化された結果を病院に返します。これにより、データのプライバシーが確保され、データ処理のニーズも満たされます。

これが完全同態暗号の魅力であり、安全かつ柔軟なデータ処理方法を提供してくれます。

なぜFHEが重要なのか？

現在、暗号化データに対する計算の既存の方法は理想的ではありません。それらはリソースの使用と時間の消費が相対的に高価です。

したがって、業界の標準プロセスは、計算を行う前に第三者（つまり企業）がデータを解読することです。

具体的な例を挙げてみましょう。あなたが高名な個人の財務情報を含むデータファイルを持っていると想像してください。

• このファイルを「M」と呼びます。私たちはある会社にこれらのデータを分析してもらう必要があります。

• 現在のプロセスはどうなっているのでしょうか？まず、私はRSAやAESのような暗号関数を使用してMを暗号化します。この時、MはE(M)に変わります。ここでEは暗号関数です。

• 次に、私はE(M)を会社のサーバーに送信します。会社は関連する解読関数Dを使用してE(M)を明文に解読します。つまりD(M)です。

• 会社はファイルMに対して明文で分析操作を行います。

• 操作が完了したら、再度Mを暗号化し、E(M')を生成します。

• 会社は暗号化されたM'を私に送り返し、私は再度それを解読します。

気づきましたか？ここでの重要な問題は、会社がMを解読し、そのサーバーに保存して計算を行うときに、第三者が本来保護されるべき敏感なデータにアクセスできることです。もしその人物がハッキングされたり悪意を持っていた場合、問題が発生します。

完全同態暗号（FHE）は、暗号化データに対して計算を行うことを許可することでこの問題を解決します。会社はもはやE(M)を解読する必要がありません。直接暗号化データ上で分析を行います。解読の必要もなく、信頼の仮定も必要ありません。

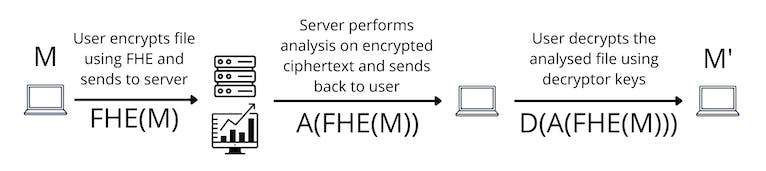
要するに、完全同態暗号の導入は、第三者がデータを処理する際にプライバシーリスクが露呈するという現在のデータ処理プロセスの重要な問題を解決しました。FHEは、データのプライバシーを保証しながら、暗号化データを効果的に処理する方法を提供してくれます。

FHEはCryptoでどのように応用されるのか？

完全同態暗号（FHE）は暗号の世界に新たな扉を開き、私たちに以前は想像できなかった多くの応用シナリオをもたらしました。Poly Ventureの原文はシナリオの説明が比較的シンプルなので、私たちは表を使ってより整理された解釈を試みます。

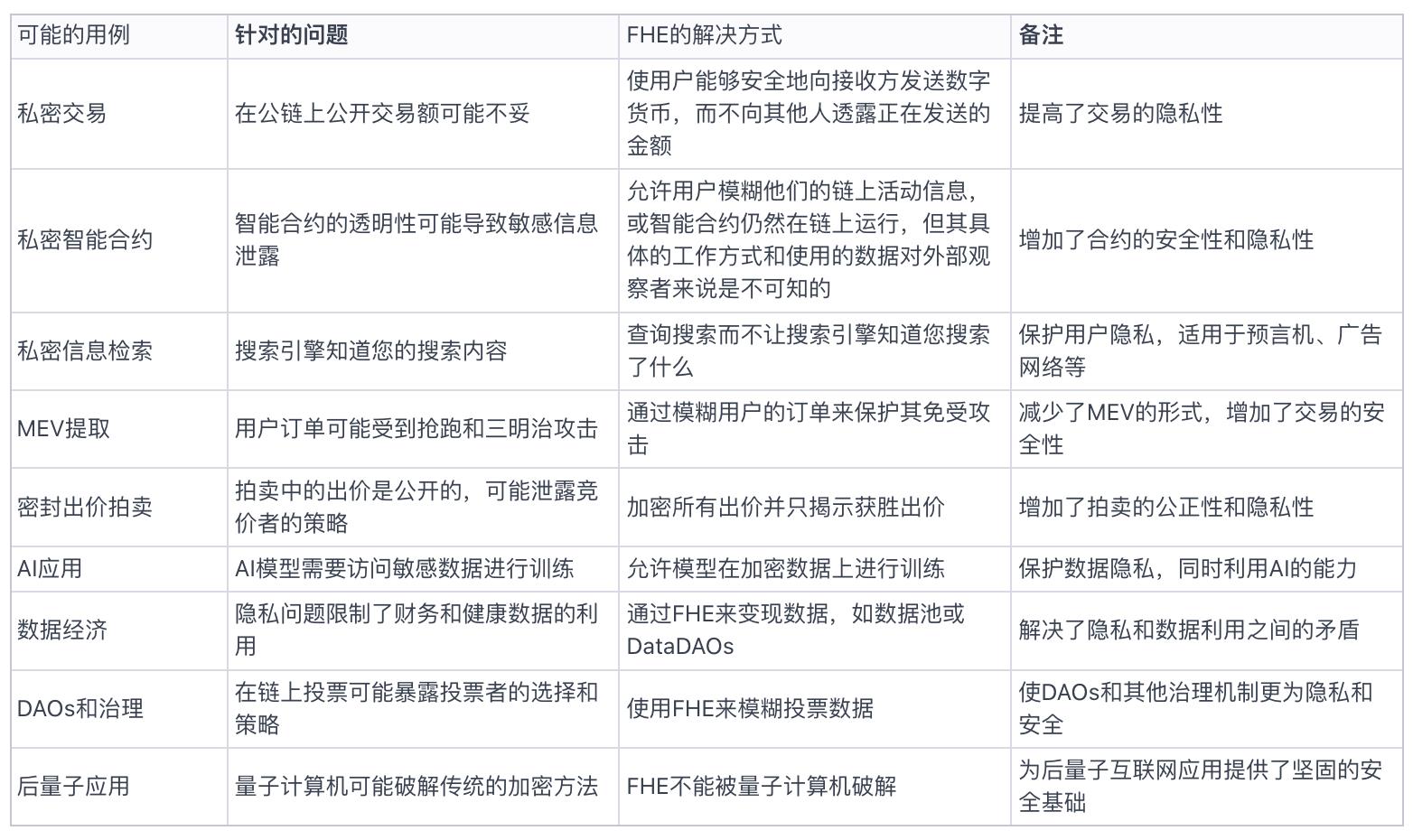
FHE vs ZK vs MPC、混同しがち？

完全同態暗号（FHE）を理解した後、ゼロ知識証明（ZK）やマルチパーティ計算（MPC）などの他の馴染みのある技術と比較するのは簡単です。一見すると、これらはすべて似たようなプライバシーと計算の問題を解決しようとしているように見えます。しかし、実際にはこれら三者の間にはどのような関係と違いがあるのでしょうか？

まず、これら三つの技術の基本的な定義を理解しましょう：

• FHE：暗号化データ上で計算を実行することを許可し、解読は不要です。

• ZK：一方が他方に対して、ある主張が真実であることを証明することを許可し、その主張に関する具体的な情報を明らかにしません。

• MPC：複数の当事者が自分のプライベートデータ上で共同で計算を行うことを可能にし、他の参加者に入力データを漏らしません。

次に、彼らの類似点と相違点を複数の次元から見てみましょう：

1. 目的：

• FHEの主な目的は、解読せずに計算を行うことです。

• ZKの目的は、事実の正確性を証明することであり、その事実に関する情報を漏らさないことです。

• MPCの目的は、複数の当事者が安全に共同計算を行うことであり、各自の入力を漏らさないことです。

1. プライバシーと計算：

• ZKでは、計算が必ずしもプライベートであるとは限りません。例えば、あなたはZKを使用して銀行口座の残高が100,000ドルを超えているかどうかを検証できますが、その検証のための計算は必ずしもプライベートではありません。

• これに対して、FHEは計算のプライバシーを確保します。すべての計算は暗号化データ上で行われます。

1. 制限と課題：

• MPCは少なくとも1つの誠実なサーバーを必要とし、DDoS攻撃、沈黙の共謀攻撃、通信コストの影響を受ける可能性があります。

• ZKは主に正確性を証明するために使用され、プライバシー技術ではありません。

• FHEは強力なプライバシーを提供しますが、計算効率が低く、リソースの要求が大きいです。

1. 暗号分野での応用：

• FHEは、よりプライバシーを重視したスマートコントラクトや他のブロックチェーンアプリケーションの構築に使用できます。

• ZKは、zk-rollupsのようなスケーラブルなブロックチェーンソリューションの作成に使用されます。

• MPCは主にプライベートキー管理とホスティングに使用されます。

1. 交差使用：

• MPCはFHEと組み合わせて閾値FHEを形成し、FHE暗号化キーを複数に分割し、各参加者に1つずつ与えることでセキュリティを強化します。

• zkFHEはゼロ知識証明と完全同態暗号の組み合わせであり、FHEスマートコントラクト上でのzk-rollupsを実現するために研究されています。

全体として、FHE、ZK、MPCはある側面で重複しているものの、それぞれ独自の利点と応用シナリオを持っています。暗号の世界では、これら三つの技術はプライバシーとセキュリティを強化するための大きな潜在能力を提供していますが、それらの組み合わせとさらなる研究は依然として暗号コミュニティの活発な分野です。

最後に、上記の技術を比較するための簡潔な表を示し、皆さんがより直感的に理解できるようにします。

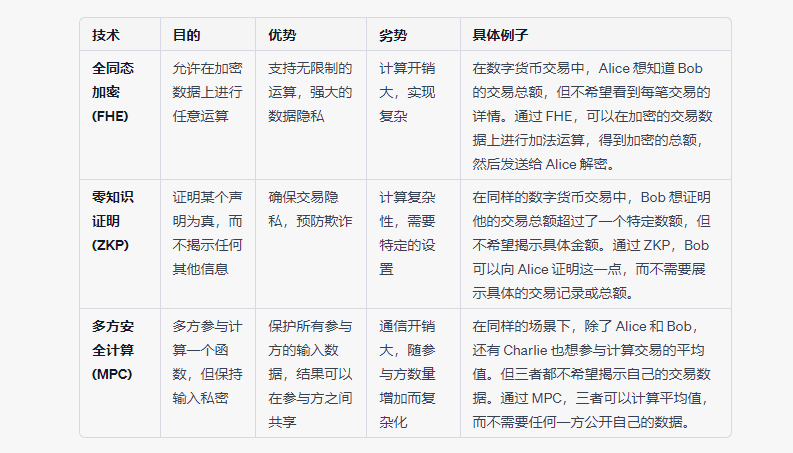
FHEの未来展望

上記の内容から、完全同態暗号（FHE）は明らかに強力な技術であることが感じられます。

しかし、なぜそれは広く採用されていないのでしょうか？さらには、暗号CTでほとんど言及されていないのでしょうか？一方では技術自体の理解に一定のハードルがあり、他方ではFHE技術が現在いくつかの課題に直面しており、商業化の形で一般の視野に入るのが難しいからです。

直面している課題には以下のようなものがあります：

1. 計算集約型：私たちの暗号文が相互作用する際、安全性を維持するためにより多くのノイズが追加されます。FHEスキームはノイズを減少させるために「ブートストラップ」技術を使用しますが、これは非常に計算集約型で、リソース消費が大きいです。

2. 機能の制限：FHEの計算は加算、乗算およびその変種/組み合わせに限られます。例えば、FHEではif文を使用することはできません。なぜなら、内容が暗号化されているからです。また、比較や除算のような比較的複雑な操作を構築するには、基本的なロジックを慎重に計画する必要があり、これがより複雑なプログラミング技術と計算効率の低下を引き起こします。

3. 互換性/組み合わせの問題：既存のアプリケーションやサービスプロバイダーは、暗号化データ上で計算を行うために構築されていません。これにより、FHEと既存技術の統合が制限され、FHE互換アプリケーションの開発に必要な慣性が増加します。

可能な解決策：

1. ハードウェアアクセラレーター：nuFHEやcuFHEのような一部のFHEスキームはGPUアクセラレーションを使用できますが、主な突破口はより高速なFPGAやASICから来るでしょう。他の技術、例えば光子技術もFHEのハードウェアユースケースを加速するために研究されています。

2. 新しいプログラミングパラダイム：Pythonでの複雑な数学のためのパッケージ（pandasやnumpyなど）のように、FHEライブラリも構築されるでしょう。現在、ZamaとSunscreenはFHEのためにこのようなライブラリやSDKを構築している2つのプロジェクトです。また、開発者がFHE、ZKP、MPCを統一できるようにするための専用のコンパイラも必要です。

3. FHEと既存のソリューションの統合：既存のツールとFHEを互換性を持たせるソリューションを構築し、ツールとFHE暗号化データの間の中間層として機能させます。

最後に、Portal Venturesは原文の結論部分で再度強調しています：

"FHEは計算の聖杯であり、私たちはその商業化に近づいています。価値と計算はオープンで許可不要のネットワークに移行しており、私たちはFHEが必要なインフラとアプリケーションの大部分を支えると信じています"。

さらに、彼らは現在FHEを研究しているプロジェクトに対する関心を表明しています。したがって、私たちが見ることができるのは、VCがFHEに興味を持っているか、あるいはVCが一般の視野に入っていないハードコア技術に最初に興味を持つということです。

歴史は、新技術に基づく暗号プロジェクトがしばしば輝かしい光環と高い評価を持ち、さまざまな資本からの注目を集めることを示しています。

次の盛宴が始まる前に、私たちは確かにもっと時間をかけて、入場者の身元を事前に研究し、宴会が始まるときにうまく対処できるようにするべきです。