インタラクティブな証明を非インタラクティブに変換するにはどうすればよいですか？

著者：康水跃、Fox Tech CEO；孟铉济、Fox Tech 首席科学家

前言

暗号学におけるゼロ知識証明技術は、web3の世界で広く応用されており、プライバシー計算やzkRollupなどが含まれます。その中で、Layer2プロジェクトFOXが使用するFOAKSは、ゼロ知識証明アルゴリズムの一つです。これらの一連の応用において、ゼロ知識証明アルゴリズムにとって特に重要な属性が二つあります。それは、アルゴリズムの効率性と相互作用性です。

アルゴリズムの効率性の重要性は言うまでもなく、高効率のアルゴリズムはシステムの実行時間を明らかに短縮し、クライアントの遅延を低下させ、ユーザー体験と効率を大幅に向上させることができます。これがFOAKSが線形証明時間を実現することに注力している重要な理由の一つです。

一方、暗号学の観点から見ると、ゼロ知識証明システムの設計は、しばしば証明者と検証者の多段階の相互作用に依存します。例えば、多くのゼロ知識証明を紹介する普及記事で使用される「ゼロ知識の洞窟」の物語では、証明の実現はアリババ（証明者）と記者（検証者）の間の多段階の情報伝達の相互作用に依存しています。しかし実際には、多くの応用シーンにおいて、相互作用に依存することはシステムの利用可能性を損ない、または遅延を大幅に増加させることになります。zkRollupシステムのように、私たちは証明者（FOXのフォルダー）がローカルで、検証者との相互作用に依存せずに正しい証明値を計算できることを期待しています。

この観点から、相互作用型のゼロ知識証明プロトコルを非相互作用型に改造する方法は非常に意義のある問題です。本記事では、FOXが古典的なFiat-Shamirヒューリスティックを使用してBrakedownの挑戦を生成し、非相互作用型プロトコルを実現するプロセスを紹介します。

ゼロ知識証明におけるChallenge

ゼロ知識証明アルゴリズムは応用の拡大に伴い異常に人気が高まり、近年ではFOAKS、Orion、zk-starkなどのさまざまなアルゴリズムが誕生しました。これらのアルゴリズムや暗号学界の初期のsigmaプロトコルなどの核心的な証明論理は、証明者（Prover）が最初に特定の値を検証者（Verifier）に送信し、検証者がローカルの乱数を生成して挑戦（Challenge）を行い、そのランダムに生成された挑戦値を証明者に送信するというものです。証明者は本当に知識を持っていなければ、検証者の応答を高確率で行うことができません。例えば、ゼロ知識の洞窟では、記者がコインを投げ、アリババに左側から出るか右側から出るかを伝えます。「左と右」はアリババへの挑戦であり、もし彼が本当に呪文を知っていれば、要求された方向から出てくることができ、そうでなければ半分の確率で失敗します。

ここで注意すべきは、Challengeの生成が非常に重要なステップであり、二つの要件があります。ランダム性と証明者による予測不可能性です。第一に、ランダム性はその確率的特性を保証します。第二に、もし証明者が挑戦値を予測できるなら、プロトコルの安全性が損なわれることになります。証明者が知識を持っていなくても検証を通過できることになります。たとえば、アリババが記者にどちらの側から出るかを予測できれば、呪文を知らなくても事前にその側に入ることができ、結果的にプロトコルを通過することができます。

したがって、私たちは証明者が自分のローカルで予測不可能な乱数を生成でき、かつそれが検証者によって検証可能である方法を必要としています。これにより、非相互作用型のプロトコルを実現できます。

ハッシュ関数（Hash Function）

ハッシュ関数の名前は私たちにとってあまり馴染みがないわけではありません。ビットコインのコンセンサスプロトコルPOWにおけるマイニングの数学的問題や、データ量の圧縮、メッセージ認証コードの構築など、さまざまな場面でハッシュ関数が登場します。そして、これらの異なるプロトコルにおいて、実際にはハッシュ関数のさまざまな特性が利用されています。

具体的には、安全なハッシュ関数の特性は以下の点を含みます：

圧縮性：決定的なハッシュ関数は任意の長さのメッセージを固定長に圧縮できます。

有効性：入力xが与えられたとき、出力h（x）を計算するのは容易です。

耐衝突性：入力x1が与えられたとき、別の入力x2を見つけること、すなわちx1≠x2でh（x1）= h（x2）を見つけるのは困難です。

注意すべきは、ハッシュ関数が耐衝突性を満たす場合、必然的に単方向性も満たすということです。つまり、出力yが与えられたとき、h（x）= yを満たすxを見つけることは困難です。暗号学において、理論的に絶対的に単方向性を満たす関数を構築することはできませんが、ハッシュ関数は実際の応用において基本的に単方向関数と見なすことができます。

このように、上記のいくつかの応用はそれぞれハッシュ関数の異なる特性に対応しており、さらにハッシュ関数には非常に重要な役割があり、それはランダム性を提供することです。暗号学理論で要求される完璧な乱数生成器は現在も構築できませんが、ハッシュ関数は実際にこの役割を果たすことができ、これが後述するFiat-Shamirヒューリスティックの技術の基盤を提供します。

Fiat-Shamir ヒューリスティック（Heuristic）

実際、Fiat-Shamirヒューリスティックはハッシュ関数を利用して前に生成されたスクリプトにハッシュ演算を行い、その結果得られた値を挑戦値として使用します。

ハッシュ関数Hをランダム関数と見なすと、挑戦は均等にランダムに選ばれ、証明者の公開情報やコミットメントに依存しません。安全性の分析では、アリスはHの出力を予測できず、オラクルとして扱うことしかできません。この場合、アリスがプロトコルに従わずに正しい応答を行う確率（特に必要な秘密を知らない場合）は、Hの値域の大きさに反比例します。

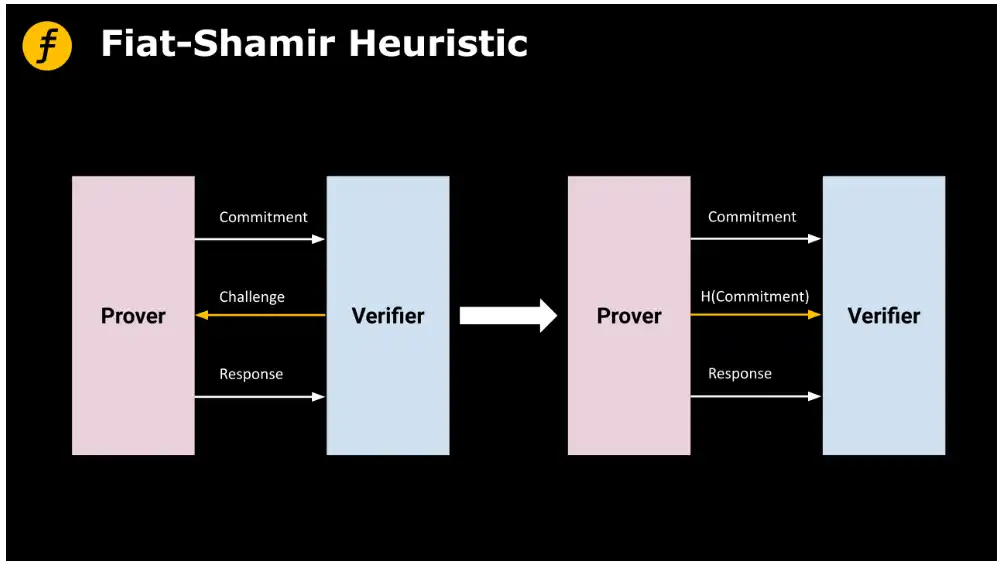
図 1: Fiat-Shamirヒューリスティックを利用した非相互作用型証明の実現

このセクションでは、FOAKSプロトコルにおけるFiat-Shamirヒューリスティックの具体的な応用を示します。主にBrakedown部分の挑戦を生成するために使用され、非相互作用型のFOAKSを実現します。

まず、Brakedownで証明を生成するステップにおいて、挑戦が必要なステップは「近似性検証」とMerkle Treeの証明部分です（読者は以前の記事「一文了解 FOAKS 当中的多项式承诺协议 Brakedown」を参照できます）。第一の点では、元々のプロセスでは証明者がここで検証者に生成されたランダムベクトルを検証する必要があります。計算プロセスは以下の図に示されています：

図 2: 非相互作用証明FOAKSにおけるBrakedownチェック

現在、私たちはハッシュ関数を使用して、証明者がこのランダムベクトルを自ら生成します。

0=H(C1,R, r0,r1)とし、対応して、検証者の検証計算においてもこの0を計算するステップを追加する必要があります。このような構造により、証明者はコミットメントを生成する前に挑戦値を予測できず、したがって挑戦値に基づいて「不正」を行うことができません。また、ハッシュ関数の出力のランダム性により、この挑戦値もランダム性を満たします。

第二の点では、I=H(C1,R, r0,r1,c1,y1,c0,y0)とします。

以下に擬似コードを示し、改造後の非相互作用型Brakedown多項式コミットメントにおける証明と検証関数を示します。これもFOAKSシステムで使用される関数です。

function PC. Commit()：

wをkk行列として解析します。証明者はローカルでテンソルコードエンコーディングC1，C2を計算します。C1はkn行列、C2はnn行列です。

for i [n] do

MerkleツリーのルートRoott=Merkle.Commit(C2[:,i])を計算します。

MerkleツリーのルートR=Merkle.Commit([Root0,……Rootn-1])を計算し、Rをコミットメントとして出力します。

function PC. Prover(, X, R)

証明者は次のように計算してランダムベクトル0Fkを生成します：0=H(C1,R, r0,r1)

近似性：c0=i=0k-10[i]C1[:,i],y0=i=0k-10[i]w[i]

一貫性：c1=i=0k-1r0[i]C1[:,i],y1=i=0k-1r0[i]w[i]

証明者はc1,y1,c0,y0を検証者に送信します。

証明者はIを挑戦として計算し、I=H(C1,R, r0,r1,c1,y1,c0,y0)とします。

for idxI do

証明者はC1 [:,idx]とMerkleツリーのRootidxの証明をRの下でC2 [:,idx]に対して検証者に送信します。

function PC. VERIFY_EVAL(X,X,y=(X),R)

近似性：idxI,C0[idx]==\<0,C1[:,idx]>およびEC(y0)==C0

一貫性：idxI,C1[idx]==\<r0,C1[:,idx]>およびEC(y1)==C1

y==\<r1, y1>

idxI, EC(C1[:,idx])はROOTidxと一致し、ROOTidxのMerkleツリーの証明は有効です。

すべての条件が満たされていれば受け入れ、そうでなければ拒否します。

结语

多くのゼロ知識証明アルゴリズムは設計当初から証明者と検証者の相互作用に依存していますが、このような相互作用型証明プロトコルは、高効率でネットワーク通信コストが大きいアプリケーションシーンには適していません。例えば、オンチェーンデータのプライバシー保護やzkRollupなどです。Fiat-Shamirヒューリスティックを通じて、プロトコルの安全性を損なうことなく、証明者がローカルでランダム数「挑戦」を生成し、かつそれが証明者によって検証可能になります。この方法に基づいて、FOAKSも非相互作用型の証明を実現し、システムに応用されています。