This article will introduce the third section of Arweave's latest white paper. This part mainly explains some fundamental concepts to lay the groundwork for the introduction of subsequent mechanisms. Originally, this section also included the mechanism proof of SPoRes, but since it consists entirely of formulas and mathematical derivations, the author feels that it might be more reasonable to interpret it separately.

Arweave's mining mechanism combines many different algorithms and data structures into a non-interactive and concise proof of data replication storage. In this article, we will first abstractly understand the concept of the mechanism and then describe their use in the Arweave mining process.

White paper link: https://www.arweave.org/files/arweave-lightpaper.pdf

Block Index

The highest data structure in Arweave is called the Block Index. It is a Merkleized list composed of 3-tuples, where each tuple contains information in three dimensions: A Block Hash, A Weave Size, and A Transaction Root. This list is represented in the form of a hash Merkle tree, with the top-level Merkle root representing the current latest state of the network. This root is composed of the hash of two elements—the latest tuple (representing the latest block) and the Merkle root of the previous block index. When creating a block, miners embed the Merkle root of the previous block index into the new block.

By constructing and embedding a Merkle root of the block index in each block, an Arweave network node that has performed an SPV proof on the latest block can fully verify any previous blocks. This contrasts with traditional blockchains, where validating transactions in old blocks requires backtracking through the entire chain for complete verification. In Arweave, after performing SPV verification on the top of the network, the block index verification mechanism allows users to verify old blocks in the weave network without needing to download or verify intermediate block headers.

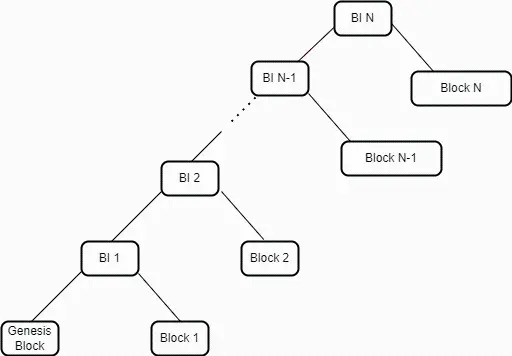
Figure 1: The block index represents a Merkle tree of blocks in the Arweave network.

Merkleized Data

So how is data stored in the network?

When information needs to be stored in Arweave, the data is split into chunks of 256 KB according to specifications. Once these chunks are ready, a Merkle tree is constructed, and its root (called the Data Root) is submitted to the transaction. This transaction is signed and sent to the network by the uploader. Each transaction constructed this way is recorded in the transaction root of its respective block. Therefore, the transaction root of a block is actually the Merkle root of the transaction data roots.

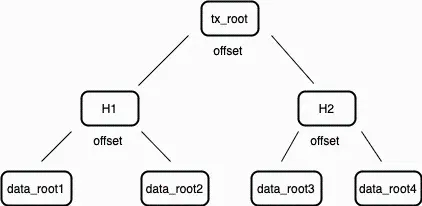
Figure 2: The transaction root is the Merkle root of the data roots present in each transaction within the block.

Miners combine such transactions into a block, calculate the transaction root using the data roots within the transactions, and include this transaction root in the new block. This transaction root will ultimately appear in the top-level block index. This process creates an ever-expanding Merkle tree, where all data is sequentially divided into chunks.

Succinct Proof of Access (SPoA)

In the Arweave network, nodes in the Merkle tree label data chunks by marking their offset positions as "left" or "right" of the node. This method of labeling nodes can generate very concise Merkle proofs to verify the existence of data chunks at specific positions in the dataset. Such Merkle trees are called "unbalanced trees" because the number of leaf nodes on one side may not equal that on the other side. This structure can be used to build a succinct non-interactive proof game to verify that the corresponding data indeed exists on the miner's hard drive.

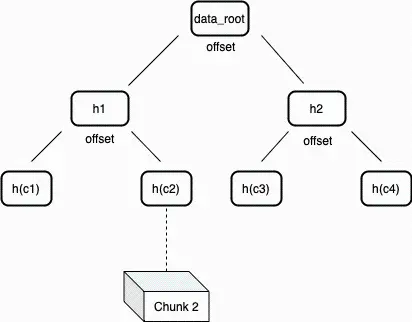
Figure 3: The data root is the Merkle root of all data chunks hashed in a single transaction.

We can understand what a Succinct Proof of Access (SPoA) is through a game between Bob and Alice. Bob wants to verify whether Alice has stored data at a specific position in a Merkleized dataset. To start the game, Bob and Alice should have the Merkle root of the same dataset. The game consists of three stages: challenge, proof construction, and verification.

• Challenge: Bob sends Alice an offset of a data chunk (it might be clearer to think of it as the position coordinates of the data chunk) to initiate the challenge—Alice needs to prove that she can access the data at this indexed position.

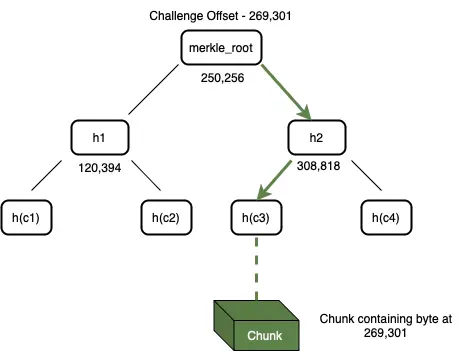
Figure 4: Alice can search for the challenged data chunk by traversing the Merkle tree labeled with the offset.

• Constructing Proof: Upon receiving the challenge, Alice begins to construct the proof. She searches her Merkle tree to find the data chunk corresponding to the offset, as shown in Figure 4. In the first phase of constructing the proof, Alice retrieves the entire data chunk from storage. Then, she uses this data chunk and the Merkle tree to construct a Merkle proof path. She hashes the entire data chunk to obtain a 32-byte string and finds the parent node of this leaf node in the tree. The parent node is a node that contains its offset and the hash values of two child nodes, each 32 bytes long. This parent node is added to the proof. She then recursively adds each upper parent node to the proof until reaching the Merkle root. This series of nodes forms the Merkle path proof, which Alice sends to Bob along with the data chunk.

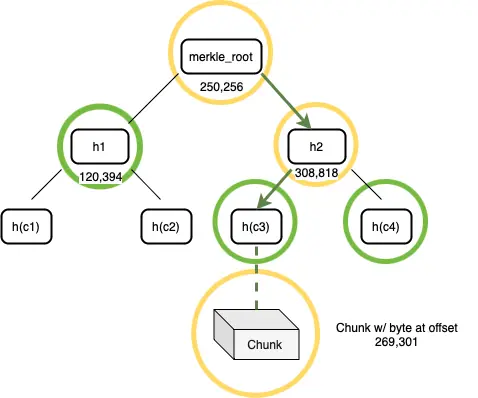
Figure 5: A proof for a challenge offset includes the data chunk stored at the offset and its Merkle path.

• Verification: Bob receives the Merkle proof and data chunk from Alice. He verifies the correctness of the Merkle proof by checking the hash values from the top of the tree down to the leaf. Then, he hashes the data chunk provided by Alice in the proof to confirm whether this data chunk is indeed the one located at the correct position. If all these hash values match, the proof is valid. However, if any hash value does not match during the verification process, Bob will immediately stop checking and conclude that Alice's proof is invalid. The result of this check is a simple yes or no process, indicating whether the proof passes.

The complexity of constructing, transmitting, and verifying this Succinct Proof of Access (SPoA) is O(logn), where n represents the size of the dataset in bytes. In practice, this means that in a dataset of size 2^256 bytes, a proof of a single byte's position and correctness can be transmitted with approximately 256 * 96B (maximum path size) + 256 KB (maximum data chunk size) ≈ 280 KB.

Uniqueness of Copies

The Arweave network designs mining capability to be proportional to the number of unique copies of the weave network that miners (or a group of cooperating miners) can access. Without a copy uniqueness scheme, backups of a piece of data are entirely identical in content. To incentivize and measure multiple unique copies of individual data, Arweave employs a packing system to address this issue.

Packing

The packing mechanism ensures that miners cannot forge multiple SPoA proofs using the same data chunk. Arweave references the RandomX packing scheme, which converts the original data chunk into "packed" data chunks, incurring a certain computational cost for miners.

The packing process is as follows:

• The data chunk offset, transaction root, and mining address are used in a SHA-256 hash to generate a Packing Key.
• The Packing Key is used as entropy for an algorithm that generates a 2 MB buffer after several rounds of RandomX execution. This component of the packing mechanism imposes significant costs on miners who do not comply with the rules.
• The first 256 KB of this entropy is used to symmetrically encrypt the chunk using a Feistel cipher, producing a packed data chunk.

If the total cost of reading packed data chunks exceeds the cost of storing the packed data chunks within a continuous reading time period, miners will be incentivized to store unique data chunks rather than packing data chunks on demand. Therefore, to incentivize this correct behavior, the following condition must be met:

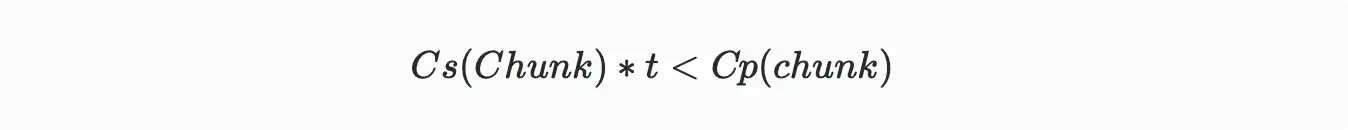
Where:

Cs = the unit time cost of storing a data chunk

Cp = the cost of packing a data chunk

t = the average time between data chunk reads

The total packing cost includes the power cost required for computation, the cost of specialized hardware, and its average lifespan. The storage cost can also be calculated from the cost of hard drives, average failure time of hard drives, power costs for running hard drives, and other costs associated with operating storage hardware. We can calculate the cost ratio between "on-demand" speculative miners and honest miners storing packed data chunks to estimate the safety margin for incentivizing packed data chunks. In practice, Arweave uses a safety ratio—specifically, the cost ratio of on-demand speculative mining to the cost of honest data storage mining—which, at the time of writing, is approximately 19:1.

RandomX

To resist hardware acceleration strategies, Arweave employs the RandomX hashing algorithm to process the Packing Key. RandomX is optimized for general-purpose CPUs and significantly limits the computational efficiency of specialized hardware such as GPUs and ASICs by implementing random code execution and various memory-intensive techniques during the hashing process.

RandomX utilizes randomly generated programs that are highly matched to the hardware characteristics of general-purpose CPUs, meaning that the only way to increase the speed of RandomX hashing is to develop faster general-purpose CPUs. This may theoretically motivate the development of faster CPUs, but in practice, this incentive is almost negligible compared to existing motivations to increase CPU speed.

Verifiable Delay Function (VDF)

A Verifiable Delay Function (VDF) acts like a verifiable cryptographic digital clock, allowing for the computational verification of the passage of time between events. VDF requires a specified number of sequential, non-parallel hash computations to produce a unique output that can be efficiently verified. The Arweave protocol uses a technique called Hash Chain to generate VDF, which is recursively defined as:

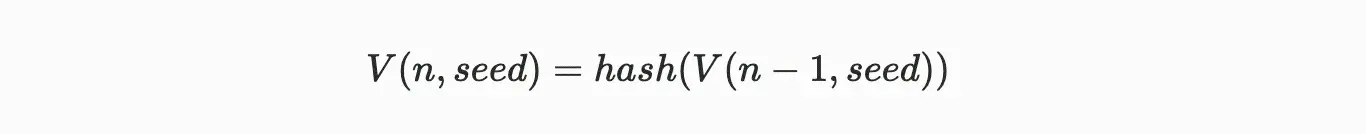
Formula annotation: The n-th VDF hash is a re-hashing of its previous VDF hash.

For n = 1:

Formula annotation: If n=1, the first VDF hash is the hash computation of the seed.

The hash function used in Arweave VDF is SHA2-256. Through this structure, if the fastest CPU on the market can continuously compute k SHA2-256 hashes per second, then performing V(k,seed) computation on a seed will take at least 1 second. This is a continuous hashing process, as shown in the formula above; when n=1, the seed is hashed, and when n=2, V(2,seed) is the hash of V(1,seed), and so on. A correctly generated V(k,seed), known as a checkpoint, indicates that at least 1 second has passed between the prover receiving the seed and generating this checkpoint.

If the VDF structure requires O(n) time to complete n steps of computation, then the verifier can use p parallel threads to complete the verification of the VDF output in O(n/p) time. It is important to note that VDF generation should not use parallel thread computation, but verification can, which allows the verification process to become faster and more efficient. We use the chain hash VDF because of its simple structure and its characteristic of being entirely reliant on the robustness of the hash function.