Foresight Ventures: The Cancun upgrade is coming, which L2s have made adaptations?

Author: Maggie@Foresight Ventures

TL;DR：

• The Cancun upgrade will be launched on March 13, 2024, and EIP4844 is about to go live. Danksharding is at the core of Ethereum's roadmap, and this upgrade is the first step towards implementing Danksharding.
• After Ethereum L2 adapts to EIP4844, transaction fees will drop significantly, and L2's TPS will increase exponentially. Users will experience faster transaction speeds, lower costs, smoother experiences, and more responsive interactions. More complex and larger Dapp applications will emerge on these L2s.
• Adapting Optimistic rollups to EIP4844 is simpler, while adapting ZK rollups is more complex. Ethereum lacks precompiled contract support for the BLS12-381 elliptic curve, making some ZKP verifications difficult and hindering the progress of ZK rollups adapting to EIP4844.
• The elliptic curve issue can be resolved in two ways: 1. Wait for Ethereum to precompile the BLS12-381 elliptic curve; 2. Use another proof method to achieve the same purpose, utilizing the BN254 supported by Ethereum's precompiled contracts.
• Currently, Arbitrum, Optimistic, Starknet, zkSync, Scroll, Polygon zkEVM, and the new L2 Morph are all adapting to EIP4844. Among them, Arbitrum, Optimistic, and Starknet have indicated that they will implement adaptations to EIP4844 after the Cancun upgrade. Morph has taken the lead in releasing an innovative zkSNARK zkEVM adaptation plan, making it the first zkSNARK zkEVM to adapt to EIP4844.

I. Background

In 2020, Ethereum released the "Rollup-Centric Ethereum Roadmap," and the vision for Ethereum's endgame described by Vitalik the following year, established the general direction for Ethereum: optimizing the foundational layer of Ethereum to serve Rollups.

Ethereum designed the Danksharding sharding technology to enhance its usability as a data availability layer. It will significantly reduce L2 transaction fees, increase Rollup TPS, and achieve substantial scalability for Ethereum.

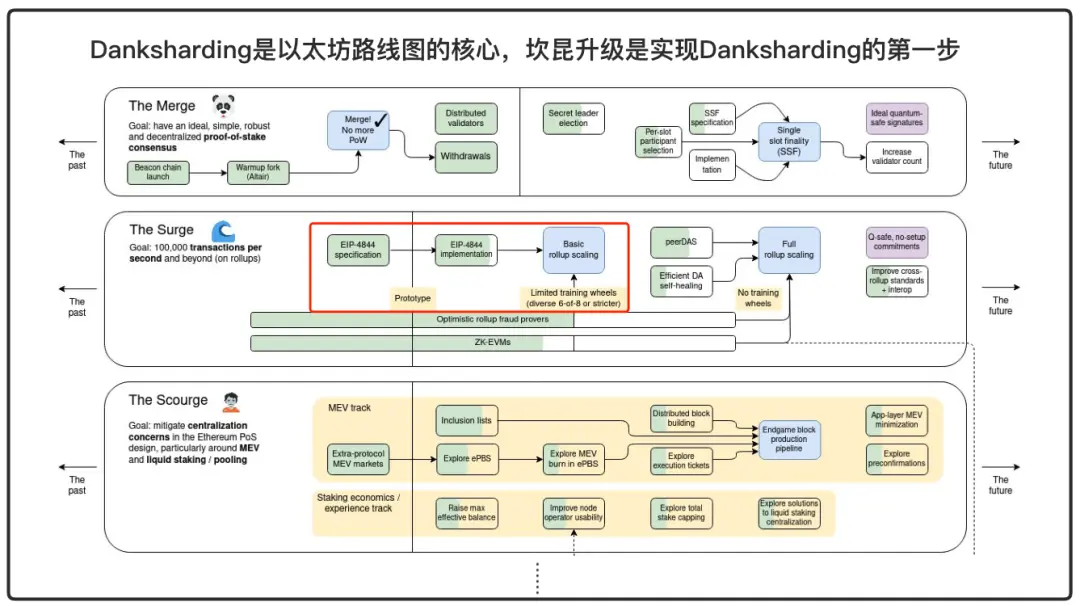
Until this year, the Ethereum Cancun-Dencun upgrade is finally set to launch on March 13, 2024, with EIP4844 about to go live. This hard fork can be considered the first step for Ethereum to achieve Danksharding and is at the core of Ethereum's roadmap. For information on what the DA layer is, the technical principles of Danksharding, and the content of EIP4844, please refer to a technical article I wrote last year: Is DA (Data Availability) Summer Coming? https://foresightnews.pro/article/detail/33575

II. How Does the Cancun Upgrade Benefit L2?

EIP4844 introduces a new transaction type called blob-carrying transactions. Each blob-carrying transaction can "carry" a list of Blobs. A Blob is a data packet of about 125 KB. Blobs are stored for a short time, only 4096 epochs, slightly more than 18 days.

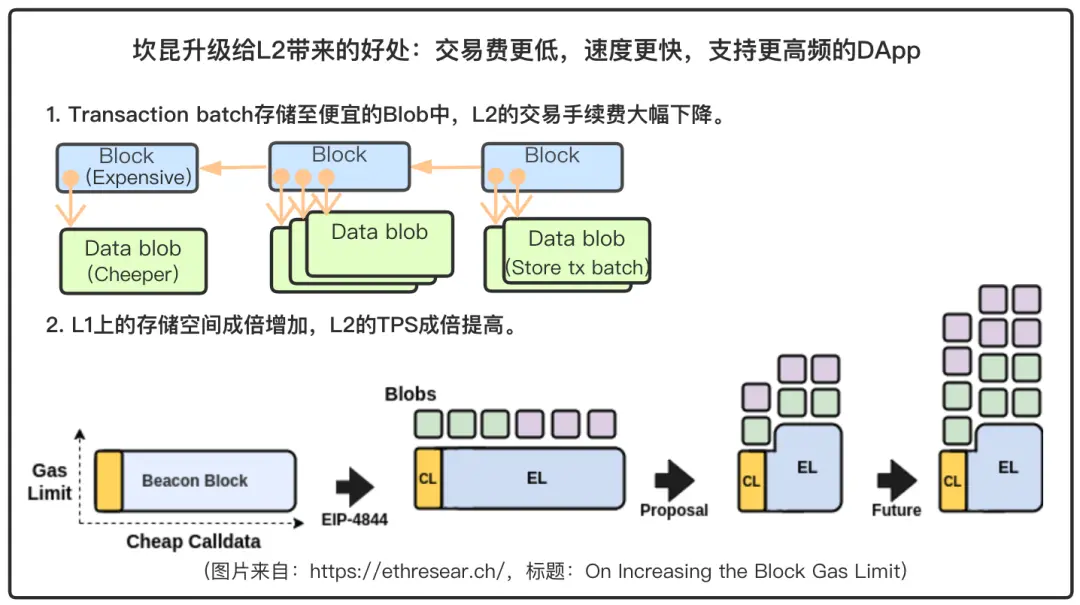
1. L2 transaction fees will drop significantly. Since Blobs do not need to be stored permanently, they are larger and cheaper compared to block space. Blobs can store 10 times more data than Calldata at the same gas consumption. Rollups that adapt to EIP4844 can store transaction data in Blobs, reducing transaction costs by an order of magnitude.
2. L2's TPS will increase exponentially. Currently, the target for each block is 3 Blobs, with a maximum of 6 Blobs allowed. The block size is only 90KB, while each Blob is about 125KB. Introducing Blobs effectively expands the space available for storing Rollup data several times, thus exponentially increasing Rollup TPS. Additionally, Toni and Vitalik's "On Increasing the Block Gas Limit" indicates that by increasing the block gas limit and the price of non-zero Calldata bytes, smaller and less variable block sizes can be achieved, allowing for more Blobs in the future. More Blobs mean larger storage capacity.

For end users, after Ethereum L2 adapts to EIP4844, transaction speeds will be faster, costs lower, experiences smoother, and interactions more responsive. More complex and larger Dapp applications will emerge on these L2s.

III. How Do L2s Adapt to EIP4844?

How do L2s adapt to EIP4844? We need to discuss Optimistic Rollups and ZK Rollups separately.

Optimistic Rollups Adapting to EIP4844

Optimistic rollups ensure the correctness of rollup execution through fraud proofs. Nodes initially assume that state transitions are correct unless someone initiates a fraud proof within a specified time frame, proving that the previously submitted state transition is invalid, in which case the state transition will be revoked.

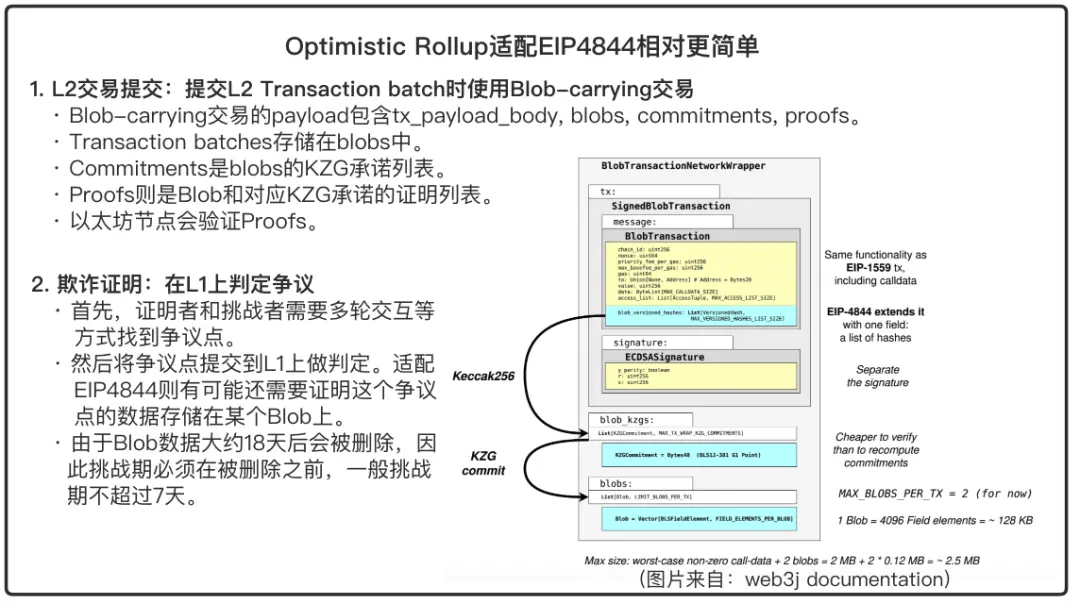
Adapting Optimistic Rollups to EIP4844 is relatively simpler than ZK rollups. All L2 transactions can be submitted to L1 through blob-carrying transactions. Additionally, adjustments to the fraud proof will be necessary to adapt to EIP4844, which can be done gradually. After all, many optimistic rollups have yet to launch fraud proofs. For those that have launched fraud proofs, none have submitted a fraud proof in over two years.

1. L2 Transaction Submission: When Rollup submits, it uses blob-carrying transactions to store Rollup data in Blobs. The payload of a blob-carrying transaction is rlp([tx_payload_body, blobs, commitments, proofs]), where

• txpayloadbody - is the standard EIP-2718 blob transaction's TransactionPayloadBody.
• blobs - Blob list. A transaction can contain a maximum of two blobs.
• commitments - List of KZG commitments for the Blobs.
• proofs - List of proofs for the Blobs and corresponding KZG commitments. This proof will be verified by ETH nodes.

1. Adjusting Fraud Proofs:

• First, the prover and challenger need to find points of contention through multiple rounds of interaction.
• Then, the points of contention are submitted to L1 for determination. Adapting to EIP4844 may also require proving that the data for this point of contention is stored in a specific Blob.
• Since Blob data will be deleted after about 18 days, the challenge period must occur before deletion, which current optimistic rollups satisfy. Generally, the challenge period does not exceed 7 days.

ZK Rollups Adapting to EIP4844

ZK rollups prove that L2 state transitions are correct through ZKP. Adapting ZK rollups to EIP4844 is more complex than adapting Optimistic rollups.

1. L2 Transaction Submission: This step is similar to Optimistic Rollups.

2. ZK Proof Submission: In addition to generating the ZKP proof for state transitions, it is necessary to prove that the blob commitment corresponds to the transaction batch, ensuring that the input for the state transition proof is correct.**

   For example: The ZK circuit for state transitions can generate a proof for the computation process a + a = b. When (a=1, b=2) and (a=2, b=4), the generated ZKP is valid. Therefore, I also need to provide a proof that the input I provided at that time was (a=1, b=2) and not (a=2, b=4).

   This was not necessary before adapting to EIP4844, as the data was directly stored in Calldata and could be read directly, ensuring that the input would not be tampered with. After using EIP4844, Blob data cannot be read directly and can only be proven through a new circuit.

   Using STARK's ZK rollup (like Starknet) makes it easier to implement this proof mechanism. However, this poses challenges for ZK rollups using SNARKs because the elliptic curve used for EIP4844's blob commitment is BLS12-381, while Ethereum's precompiled contracts only support BN254. Due to the different curves, it is difficult to directly verify blob commitments in smart contracts.

3. ZK EVM/zkVM using SNARKs need to address the issue mentioned in point 2 regarding the inability to generate ZK proofs due to curve mismatch.

• Wait for Ethereum to support precompiled contracts for BLS12-381. This will take a long time.
• Use another proof method to prove it. A new circuit must be designed using the BN254 elliptic curve supported by precompiled contracts. Currently, we see that Morph has adopted this method. This also makes Morph the first zkEVM to complete the adaptation to EIP4844.

For Morph's EIP-4844 zkEVM integration solution, see: https://medium.com/@morphlayer2/morphs-solution-to-eip-4844-zkevm-integration-7f469910478f

IV. Which L2s Have Adapted to EIP4844?

Adapting Optimistic rollups to EIP4844 is relatively easy.

• Arbitrum will launch the Arb OS20 upgrade on March 14 to implement the EIP changes from the Cancun upgrade (article link). Arbitrum belongs to Stage 1 Rollups, where both transaction submission and fraud proofs need to adapt to EIP4844, providing relatively good security.
• Optimism will launch the Ecotone upgrade on March 14 to complete adaptation (article link). Optimistic rollups belong to Stage 0 Rollups, which currently do not have fraud proofs, making adaptation easier but with lower security. After adaptation, all superchain networks within the Op ecosystem will also benefit from EIP-4844.

In ZK rollups, the difficulty of adaptation varies between STRAK and SNARK rollups.

• Adapting STARK rollups to EIP4844 is simpler, with Starknet being a representative.
• Starknet has published an article indicating that it will implement adaptation to EIP4844 after the Cancun upgrade (article link).
• zkSync has completed the transition from SNARK to STARK proofs through the Boojum upgrade. This is also a preparation for the EIP4844 upgrade. Boojum is a STARK-based proof system. (article link)
• Adapting SNARK rollups is relatively complex.

Polygon zkEVM is expected to launch the Feijoa upgrade in May, adapting to EIP-4844. (article link) Scroll published an article last year introducing its approach to adapting to EIP4844 (article link). Most impressively, Morph, an Optimistic ZK Rollup, was the first to release a zkSNARK zkEVM adaptation plan for EIP4844, making it the first zkSNARK zkEVM rollup to complete EIP4844 adaptation (article link). Optimistic ZK Rollup combines the advantages of both types of Rollups. It optimistically assumes the correctness of the execution results submitted by the Sequencer, allowing those who doubt the results to challenge them. Only when a challenge is initiated will the prover generate ZKP to prove the correctness of the execution results. It possesses the efficiency of Optimistic rollups while also having the reliability of ZK proofs from ZK rollups.