The Power of Zero-Knowledge Proofs: A Deep Dive into zk-SNARKs

Compilation: DODO Research

Author: 0xAlpha Co-founder @DeriProtocol

Introduction

zk-SNARK, or "Zero-Knowledge Succinct Non-Interactive Argument of Knowledge," allows a verifier to confirm that a prover possesses certain specific knowledge, referred to as a witness, that satisfies a particular relation, without revealing any information about the witness itself.

• Generating a zk-SNARK for a specific problem involves the following four stages:
• Transforming the problem (or function) into an arithmetic circuit.
• Translating this circuit into a matrix representation.
• Further converting this matrix representation into a polynomial that should be divisible by a specific minimal polynomial.

Finally, this divisibility is represented in the points of an elliptic curve over a finite field, where the proof takes place.

The first three steps merely change the representation of the original statement. The final step uses homomorphic encryption to project the statement from the third step into the encrypted space, allowing the prover to confirm the mirrored statement within it. Given that this projection utilizes asymmetric encryption, it is infeasible to trace back from the statement of the third step to the original statement, ensuring zero knowledge exposure.

The mathematical background required to read this article is equivalent to the first-year algebra level of STEM students. The only potentially challenging concept may be elliptic curve cryptography. For those unfamiliar with it, it can be viewed as an exponential function with a special base, while keeping in mind that its inverse function remains unsolved.

This article will follow the following notation rules:

Matrix: Bold uppercase letters, e.g., A; explicit form written as
Vector: Lowercase letters with arrows, explicit form written as [ ]; by default, all vectors are column vectors
Scalar: Regular letters

Let's use this problem as an example:

f(x)=x\^3+x\^2+5 (1)

Suppose Alice wants to prove that she knows a . We will introduce the entire procedure that Alice needs to follow to generate a zk-SNARK for her proof step by step.
This problem may seem too simple as it does not involve control flow (e.g., if-then-else). However, converting functions with control flow into arithmetic expressions is not difficult. For example, let’s consider the following problem (or "function" in programming languages):

f(x, z):
if(z==1):
return x*x*x+x*x+5
else:
return x*x+5

It is easy to rewrite this problem as the following arithmetic expression (assuming z belongs to (0,1)), which is not much more complex than equation (1).

f(x,z)=(z-1)(x\^2+5)+z(x\^3+x\^2+5)

In this article, we will continue to use equation (1) as the basis for discussion.

Step 1: Arithmetic Circuit

Equation (1) can be decomposed into the following basic arithmetic operations:

This corresponds to the following arithmetic circuit:

We will also refer to equation (2) as a set of 4 "first-level constraints," each describing the relationship of an arithmetic gate in the circuit. Generally, a set of n first-level constraints can be summarized as a Quadratic Arithmetic Program (QAP), which will be explained next.

Step 2: Matrix

First, let’s define a "witness" vector as follows: 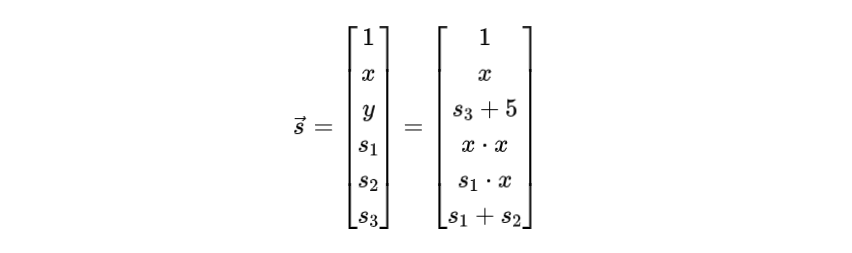where y, s1, s2, s3 are defined the same as in equation (2).
Typically, for a problem with m inputs and n arithmetic gates (i.e., n-1 intermediate steps and the final output), this witness vector will be (m+n+1)-dimensional. In practical problems, the number n can be very large. For instance, for hash functions, n is often in the thousands.

Next, let’s construct three n*(m+n+1) matrices A, B, C so that we can rewrite equation (2) as follows:

Equation (3) is merely another representation of equation (2): each group (ai, bi, ci) corresponds to a gate in the circuit. We can see this clearly by explicitly expanding the matrix equation:

Thus, LHS=RHS is entirely consistent with equation (2), where each row of the matrix equation corresponds to a first-level constraint (i.e., an arithmetic gate in the circuit).

We skipped the steps of constructing (A, B, C), which are relatively straightforward. We only need to convert them into matrix form based on the corresponding first-level constraints, determining the contents of each row of (A, B, C), i.e., (ai, bi, ci). For example, in the first row: it is easy to see that to satisfy the first first-level constraint that x multiplied by x equals s1, we need to multiply [0, 1, 0, 0, 0], [0, 1, 0, 0, 0], and [0, 0, 0, 1, 0, 0] with vector s.

Therefore, we have successfully transformed the arithmetic circuit into a matrix equation, i.e., equation (3). At the same time, we have transformed the object that needs to be proven from into the witness vector s.

Step 3: Polynomial

Now, let’s construct an n*(n+m+1) matrix PA that defines a set of polynomials in terms of z:

These are four sets of linear equations in six variables, which can be solved using traditional methods. However, a more efficient way to solve PA in this case is through Lagrange interpolation, which leverages the problem's specificity. Here we skip the process of solving PA, which, although a bit tedious, is quite straightforward.

Where:

Step 4: Elliptic Curve Points

Rewriting equation (4) as:

Where i(z)=1 is just a trivial zero-degree polynomial of z, used to unify the equation—so that all terms are quadratic. The necessity of doing this will soon become clear. Note that this equation only contains the addition and multiplication of polynomials in z.

Next, we will elaborate on the actual operational steps.

Elliptic Curve Cryptography

The general theory of elliptic curves far exceeds the scope of this article. For the purposes of this article, an elliptic curve is defined as a mapping from the prime field Fp to the function E, where E includes points that satisfy y\^2=x\^3+ax+b (referred to as elliptic curve points, or ECPs).

Note that while we have been discussing conventional arithmetic so far, now when we transition to the prime field, arithmetic operations on numbers are performed in a modular manner. For example, a+b=a+b(mod p), where p is the order of Fp.

On the other hand, the addition of two elliptic curve points is defined as shown in the figure below:

Specifically, the addition of two ECPs P and Q involves:

Finding the intersection point of the line PQ and the curve R, defined as -(P+Q)
Flipping to the "mirror" point R' on the curve R.
Thus, we define the addition of elliptic curve points P+Q=R':

Note that this rule also applies to the special case where an ECP is added to itself, in which case the tangent of that point will be used.

Now suppose we randomly select a point G and map the number 1 onto it. (This "initial mapping" may sound a bit arbitrary. It will be discussed later). Then for any n belonging to Fp, we define:

E(N)=G+ G+ G+ …..+G=G multiplied by n

This has an operational expression. Defining the operation +G as "generator," denoted as g. Then the above definition is equivalent to:

For those unfamiliar with elliptic curves, you can think of this mapping as analogous to a conventional exponential function, where the base g replaces real numbers. The behavior of arithmetic operations is similar. However, a key difference is that the inverse function of g\^n is computationally infeasible. That is, there is no way to compute the elliptic curve version of . This is, of course, the foundation of elliptic curve cryptography. Such a mapping is referred to as one-way encryption.

Note that given an elliptic curve, since the choice of G (and thus the choice of "generator" g) is arbitrary (except for points on the x-axis), there are infinitely many mapping methods. The choice (G or g) can be likened to choosing the base of an exponential function (2\^x, 10\^x, e\^x, etc.), which is part of common sense.

However, the equation (5) that Alice wants to prove is quadratic, so linear is not sufficient. To handle the quadratic terms, we need to define multiplication in the encrypted space. This is referred to as pairing functions, or bilinear mappings, which will be explained next.

Bilinear Mapping

Common Reference String

The entire process is referred to as the "Verification Key," abbreviated as VK. It involves only 7 elliptic curve points (ECPs) that need to be provided to the verifier. It is important to note that regardless of how many inputs and first-level constraints are involved in the problem, VK is always composed of 7 ECPs.

Additionally, it is worth mentioning that the "trusted setup" and the process of generating PK and VK for a specific problem only need to be performed once.

Proof and Verification

Now that Alice has the public key (PK), she will compute the following elliptic curve points (ECPs):

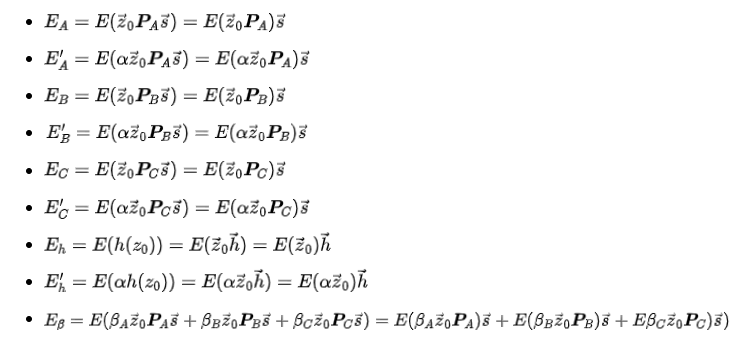
These 9 elliptic curve points are the key to the zero-knowledge succinct non-interactive proof (zk-SNARK)!

Note that Alice is actually just performing some linear combinations of the elliptic curve points in the public key. This point is particularly crucial and will be closely examined during verification.

Now, Alice has submitted the zk-SNARK proof, and we finally enter the verification phase, which proceeds in three steps.

First, it must be confirmed that the first 8 elliptic curve points are indeed linear combinations of those points in the common reference string.

If all three checks hold, then equation (5) is verified, and we believe that Alice knows the witness. Let’s explain the reasoning behind the equation. Taking the first equation from the first part as an example, the equation holds due to the bilinear property: 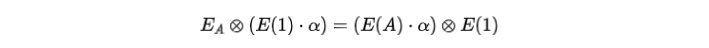However, since Alice does not know the value of the symbol alpha, she cannot explicitly compute this addition. The only way she can think of to satisfy the equation is to compute two combinations of 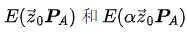using the same set of vectors s.

References

"Zk-SNARKs: Under the Hood" (Vitalik Buterin)

"A Review of Zero Knowledge Proofs" (Thomas Chen, Abby Lu, Jern Kunpittaya, and Alan Luo)

"Why and How zk-SNARK Works: Definitive Explanation" (Maksym Petkus)

Website: Zero-Knowledge Proofs

Wikipedia: Elliptic curve

Wikipedia: Finite field

Wikipedia: Pairing-based cryptography