How to transform an interactive proof into a non-interactive one?

Authors: Kang Shuaiyue, CEO of Fox Tech; Meng Xuanji, Chief Scientist of Fox Tech

Introduction

The zero-knowledge proof technology in cryptography has a wide range of applications in the web3 world, including privacy computing, zkRollup, and so on. The FOAKS used by the Layer2 project FOX is a zero-knowledge proof algorithm. Among the various applications mentioned above, two properties are extremely important for zero-knowledge proof algorithms: the efficiency of the algorithm and its interactivity.

The importance of algorithm efficiency is self-evident; an efficient algorithm can significantly reduce system runtime, thereby lowering client latency and greatly improving user experience and efficiency. This is also a key reason why FOAKS is committed to achieving linear proof time.

On the other hand, from a cryptographic perspective, the design of zero-knowledge proof systems often relies on multiple rounds of interaction between the prover and the verifier. For example, in the "zero-knowledge cave" story commonly used in many popular science articles introducing zero-knowledge proofs, the implementation of the proof relies on the multi-round information exchange between Alibaba (the prover) and the reporter (the verifier). However, in many application scenarios, reliance on interaction can render the system unusable or significantly increase latency. For instance, in a zkRollup system, we expect the prover (i.e., the folder in FOX) to compute the correct proof value locally without relying on interaction with the verifier.

From this perspective, transforming interactive zero-knowledge proof protocols into non-interactive ones is a meaningful problem. In this article, we will introduce how FOX uses the classic Fiat-Shamir heuristic to generate challenges in Brakedown to achieve a non-interactive protocol.

Challenge in Zero-Knowledge Proofs

Zero-knowledge proof algorithms have become exceptionally popular with the expansion of applications, and in recent years, various algorithms including FOAKS, Orion, zk-stark, etc., have emerged. The core proof logic of these algorithms, as well as early cryptographic sigma protocols, is that the prover first sends a certain value to the verifier, who then generates a challenge using local randomness and sends this randomly generated challenge value back to the prover. The prover must genuinely possess knowledge to respond correctly to the verifier with high probability. For example, in the zero-knowledge cave, the reporter flips a coin and tells Alibaba to come out from the left or the right; here, "left and right" is the challenge to Alibaba. If he truly knows the spell, he can certainly come out from the required direction; otherwise, he has a 50% chance of failing.

Here we note that the generation of the challenge is a critical step, with two requirements: randomness and unpredictability by the prover. The first point, randomness, ensures its probabilistic properties. The second point is that if the prover can predict the challenge value, it means the security of the protocol is compromised; the prover could pass verification without knowledge. To continue the analogy, if Alibaba can predict which side the reporter will ask him to come out from, he could enter that side in advance even without the spell, thus appearing to pass the protocol.

Therefore, we need a method that allows the prover to locally generate such an unpredictable random number, which can also be verified by the verifier, thus achieving a non-interactive protocol.

Hash Function

The name of the hash function may not be unfamiliar to us, whether it serves as a mathematical puzzle for mining in Bitcoin's consensus protocol POW, compresses data, constructs message authentication codes, etc., the hash function is present in various forms. In the aforementioned different protocols, various properties of hash functions are utilized.

Specifically, the properties of a secure hash function include the following:

• Compressibility: A deterministic hash function can compress messages of arbitrary length into a fixed length.
• Efficiency: Given an input x, computing the output h(x) is easy.
• Collision Resistance: Given an input x1, it is difficult to find another input x2 such that h(x1) = h(x2).

Note that if a hash function satisfies collision resistance, it must also satisfy one-wayness, meaning that given an output y, finding x such that h(x) = y is difficult. In cryptography, a function that theoretically satisfies absolute one-wayness has yet to be constructed, but hash functions can generally be treated as one-way functions in practical applications.

Thus, we can see that the aforementioned applications correspond to different properties of hash functions, and we can also say that hash functions play a crucial role in providing randomness. Although a perfect random number generator required by cryptographic theory cannot currently be constructed, hash functions can also serve this role in practice, laying the foundation for the Fiat-Shamir heuristic technique we will introduce later.

Fiat-Shamir Heuristic

In fact, the Fiat-Shamir heuristic utilizes hash functions to hash the previously generated script to obtain a value that serves as the challenge.

By treating the hash function H as a random function, the challenge is uniformly randomly chosen, independent of the prover's public information and commitments. Security analysis suggests that Alice cannot predict H's output and can only treat it as an oracle. In this case, the probability of Alice making a correct response without following the protocol (especially when she does not know the necessary secret) is inversely proportional to the size of H's output range.

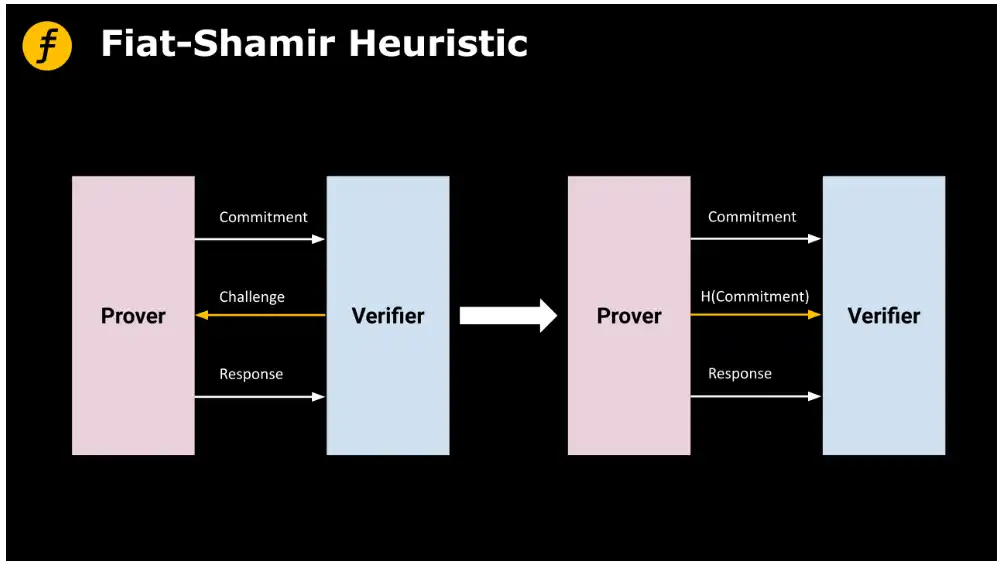
Figure 1: Achieving Non-Interactive Proof with Fiat-Shamir Heuristic in FOAKS

In this section, we specifically demonstrate the application of the Fiat-Shamir heuristic in the FOAKS protocol, mainly to generate challenges in the Brakedown section, thereby achieving non-interactive FOAKS.

First, we see that in the step of generating proofs in Brakedown, the steps requiring challenges are the "proximity check" and the proof part of the Merkle Tree (readers can refer to the previous article "Understanding the Polynomial Commitment Protocol Brakedown in FOAKS"). For the first point, the original process requires the prover to verify a random vector generated by the verifier, as shown in the following diagram:

Figure 2: Brakedown Checks in Non-Interactive Proof FOAKS

Now we use a hash function to allow the prover to generate this random vector locally.

Let 0=H(C1,R, r0,r1), correspondingly, in the verifier's verification computation, this step of calculating 0 also needs to be added. Based on this construction, it can be observed that before generating the commitment, the prover cannot predict the challenge value in advance, thus cannot "cheat" based on the challenge value, i.e., generate a false commitment value. Additionally, due to the randomness of the hash function output, this challenge value also satisfies randomness.

For the second point, let I=H(C1,R, r0,r1,c1,y1,c0,y0).

We provide pseudocode for the modified non-interactive Brakedown polynomial commitment proof and verification functions, which are also used in the FOAKS system.

function PC.Commit():
    Parse w as a kk matrix. The prover locally computes the tensor code encoding C1, C2, C1 is a kn matrix, C2 is a nn matrix.
    for i [n] do
        Compute the Merkle tree root Roott=Merkle.Commit(C2[:,i])
    Compute a Merkle tree root R=Merkle.Commit([Root0,......Rootn-1]), and output R as the commitment.

function PC.Prover(, X, R):
    The prover generates a random vector 0Fk by computing: 0=H(C1,R, r0,r1)
    Proximity: c0=i=0k-10[i]C1[:,i],y0=i=0k-10[i]w[i]
    Consistency: c1=i=0k-1r0[i]C1[:,i],y1=i=0k-1r0[i]w[i]
    Prover sends c1,y1,c0,y0 to the verifier.
    Prover computes a vector I as challenge, in which I=H(C1,R, r0,r1,c1,y1,c0,y0)
    for idxI do
        Prover sends C1[:,idx] and the Merkle tree proof of Rootidx for C2[:,idx] under R to verifier

function PC.VERIFY_EVAL(X,X,y=(X),R):
    Proximity: idxI,C0[idx]==<0,C1[:,idx]> and EC(y0)==C0
    Consistency: idxI,C1[idx]==<r0,C1[:,idx]> and EC(y1)==C1
    y==<r1, y1>
    idxI, EC(C1[:,idx]) is consistent with ROOTidx, and ROOTidx's Merkle tree proof is valid.
    Output accept if all conditions above hold. Otherwise output reject.

Conclusion

Many zero-knowledge proof algorithms initially rely on interaction between the prover and the verifier; however, such interactive proof protocols are not suitable for applications that pursue efficiency and have high network communication costs, such as on-chain data privacy protection and zkRollup. Through the Fiat-Shamir heuristic, it is possible to allow the prover to locally generate random "challenges" without compromising the security of the protocol, which can also be verified by the prover. Based on this method, FOAKS has also achieved non-interactive proof and applied it within the system.