a16z: Technical Explanation of Decentralized On-Chain Trust Setup Ceremony for Crypto Projects

Authors: Valeria Nikolaenko, Sam Ragsdale, a16z

Compiled by: Amber, Foresight News

The Trusted Setup Ceremony has always posed challenges to the crypto community, but it is undoubtedly one of the most exciting aspects for the community. The goal of the ceremony is to generate reliable cryptographic keys used to secure crypto wallets, blockchain protocols, or zero-knowledge proof systems. These procedures are the root of trust for the security of projects, making it crucial to ensure precise operations and execution of the trusted setup ceremony.

Currently, there are various forms of trusted setup ceremonies in blockchain projects, including but not limited to blowtorches, radioactive dust, and airplanes, all of which share a commonality: they rely on a centralized coordinator. This article will demonstrate how to decentralize the process by replacing the centralized coordinator with smart contracts, and we will also open-source a library that allows anyone to run what cryptographers call the Kate-Zaverucha-Goldberg (KZG) or "powers-of-tau" ceremony on Ethereum.

Our decentralized approach has limitations, but it is still useful. Due to current on-chain data constraints, the size of cryptographic parameters must remain under 64 KB. However, there is no limit to the number of participants, and anyone can submit contributions at any time. Applications of these short parameters include small zero-knowledge SNARKs, data availability sampling, and Verkle trees.

History and Mechanism of Trusted Setup Ceremonies

In a typical trusted setup ceremony, a group of participants collaborates to generate a set of cryptographic parameters. Each participant uses locally generated cryptographic information to create data that helps in forming these parameters. Proper setups can ensure that the cryptographic information does not leak, that it can only be used as specified by the protocol, and that this information is completely destroyed at the end of the ceremony. As long as at least one party in the ceremony guarantees honesty and destroys the cryptographic information (after the ceremony ends), the entire process can be considered secure. (Of course, this assumes there are no errors in the code.)

Some of the most notable ceremonies were launched by Zcash, a privacy-focused blockchain project. Participants in these ceremonies generated public parameters intended to allow Zcash users to construct and verify private encrypted transactions. Six participants held the first Zcash ceremony, Sprout, in 2016. Two years later, cryptographic researcher Ariel Gabizon, now the chief scientist at Aztec, discovered a devastating flaw in the design of the ceremony, inherited from a foundational research paper.

This vulnerability could allow an attacker to create an unlimited number of Zcash coins without detection. The Zcash team kept this vulnerability secret for seven months until the system upgrade Sapling (which involved 90 participants in its ceremony) resolved the issue. While attacks based on security vulnerabilities do not affect the privacy of user transactions, the prospect of unlimited forgery undermines the security premise of Zcash. (Theoretically, it is impossible to know if an attack occurred.)

Another notable example of trusted setup is the permanent "tau-power-of-tau" ceremony, primarily designed for Semaphore, a privacy-preserving technology for anonymous signaling on Ethereum. This setup uses the BN254 elliptic curve and has had 71 participants to date. Other notable projects later used this setup to run their own ceremonies, including Tornado.Cash, Hermez Network, and Loopring.

Aztec held a similar ceremony on the BLS12_381 elliptic curve, with 176 participants in zkSync, a "layer two" Ethereum scaling solution that uses zero-knowledge rollups. Filecoin, a decentralized data storage protocol, held ceremonies with 19 and 33 participants in the first and second phases, respectively, forking the original repository. Celo, a layer one blockchain, also held a ceremony for their lightweight client Plumo.

Permanent ceremonies have no limit on the number of participants. In other words, anyone can participate to any degree of security, rather than trusting others to run a trusted setup ceremony. A trusted participant ensures the security of all resulting parameters; a chain is only as strong as its weakest link. As the name suggests, permanent ceremonies can be held indefinitely, just like the premise of the original tau power ceremony. That is to say, projects typically decide on specific start and end times for the ceremony so they can embed the generated parameters into the protocol without worrying about constantly updating them.

Ethereum plans to run a smaller trusted setup ceremony for the upcoming ProtoDankSharding and DankSharding upgrades. These upgrades will increase the amount of data available to clients for storage on the Ethereum chain. The validity of this data is proposed to last for 30 to 60 days. The ceremony is actively being developed and is expected to run for about six weeks early next year. (See kzg-ceremony-specs for more details.) It is becoming the largest blockchain trusted setup ceremony to date.

Paranoia is a "virtue," especially when it comes to trusted setup ceremonies. If the hardware or software of the machine is compromised, it could undermine the security of the secrets it generates. Sneaky side-channel attacks that leak secrets are also difficult to rule out. For example, a phone could monitor a computer's operations by recording the sound waves of CPU vibrations. In practice, because it is challenging to eliminate all possible side-channel attacks—including those that have yet to be discovered or disclosed—some have even proposed flying machines into space to hold the ceremony there.

Currently, the script for rigorous ceremony participants typically goes as follows: purchase new machines (uncontaminated hardware). Risk isolation is achieved by removing all network cards (to prevent local secret leaks). Run the machines in a remote, undisclosed location inside a Faraday cage (to thwart potential eavesdroppers). Set a large amount of entropy and hard-copy data, such as random input or video file seeds, for the pseudo-random cryptographic information generator (to make the cryptographic information difficult to crack). Finally, destroy the cryptographic information—along with any traces of it—by burning everything to ashes.

Coordinating Trusted Setup Ceremonies

All trusted setup ceremonies rely on a centralized coordinator. The coordinator is an individual, private server, or other entity entrusted with registering and ordering participants, acting as a relay by forwarding information from one participant to the next, and maintaining a centralized log of all communications for auditing purposes. Coordinators are also typically responsible for permanently providing the logs to the public, but it must be acknowledged that such centralized systems are prone to information loss due to mismanagement or other non-human factors.

Ironically, while decentralization is a core principle of the crypto ethos, crypto projects must rely on centralized trusted setup ceremonies. Therefore, we decided to demonstrate the feasibility of holding a small ceremony for the perpetual powers-of-tau directly on the Ethereum blockchain. This setup is fully decentralized, permissionless, censorship-resistant, and secure as long as any one participant is honest. At current prices, the cost to participate in the ceremony ranges from $7 to $400, depending on the size of the desired resulting parameters (in this case, between 8 and 1024 powers of tau).

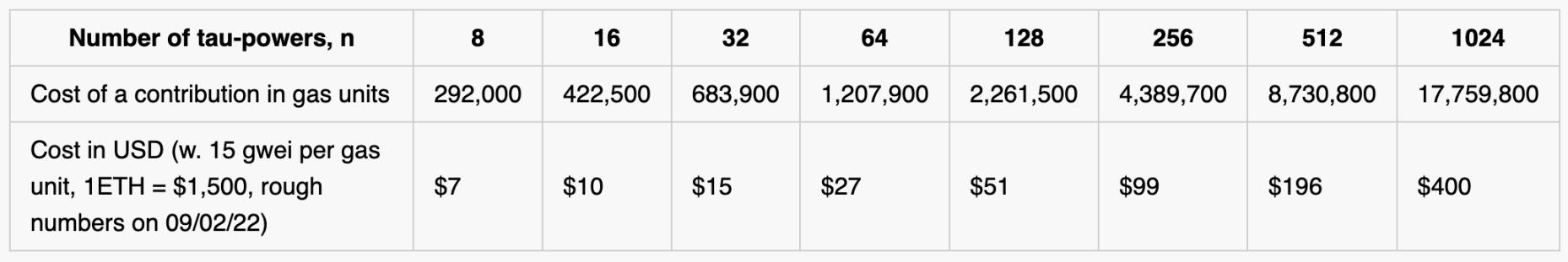
So far, we recommend not using the code for any purpose other than experimentation. We would appreciate it if anyone who discovers any issues with the code reports them to us. We are eager to collect feedback and audits regarding our approach.

Understanding the KZG or "powers-of-tau" Ceremony

Let’s explore one of the most popular trusted setups, known as KZG, or the "powers-of-tau" ceremony. Thanks to Ethereum co-founder Vitalik Buterin, his blog post on trusted setups informed our thoughts in this section. This setup generates encodings of powers-of-tau, named so because "tau" is the variable used to represent the secret generated by participants:

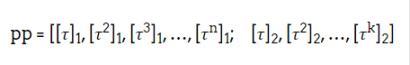For certain applications (such as Groth16, a popular zkSNARK proof scheme designed by Jens Groth in 2016), the first phase of the setup is followed by a second phase, which is a multi-party computation (MPC) ceremony that generates parameters for specific SNARK circuits. However, our work focuses solely on the first phase. The first phase—generating powers of tau—can already serve as a foundational building block for general SNARKs (such as PLONK and SONIC) and other cryptographic applications (such as KZG commitments, Verkle trees, and data availability sampling).

Generally, universal SNARK parameters should be very large so that they can support large and useful circuits. Circuits with more gates are typically more useful because they can capture large computations; the number of powers of tau roughly corresponds to the number of gates in the circuit. Therefore, a typical setup size is |pp|= ~40 GB, capable of supporting circuits of ~2^28 Gas. Given Ethereum's current constraints, placing such large parameters on-chain is not feasible, but smaller trusted setup ceremonies useful for small SNARK circuits, Verkle trees, or DAS can run on-chain.

The Ethereum Foundation plans to run several smaller ceremonies for powers-of-tau sized between 200 KB and 1.5 MB. While larger ceremonies may seem better, considering that larger parameters can create more useful SNARK circuits, in reality, bigger is not always better. Certain applications (like DAS) specifically require a smaller setup! The reasons are quite technical, but if you're curious, it's because setups with n powers (in G) 1) only allow KZG commitments to ≤ n degree polynomials, which is crucial for ensuring that polynomials under KZG commitments can be reconstructed from any n evaluations.

This property supports data availability sampling: each time a successful random evaluation of a polynomial is obtained (sampled), it guarantees that the polynomial can be completely reconstructed with probability t/n. If you want to learn more about DAS, check out Buterin's article on the Ethereum research forum.

We designed a smart contract that can be deployed on the Ethereum blockchain to run the trusted setup ceremony. This contract fully stores public parameters on-chain and collects participation through user transactions.

New participants first read these parameters:

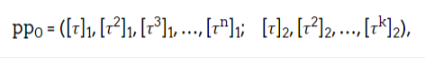
Then sample a random key τ' and compute updated parameters:

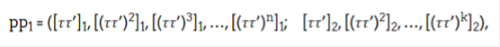
And publish them on-chain, along with proofs of three things:

• Knowledge of discrete logarithm: the participant knows τ'. (This proves that the latest contribution to the trusted setup ceremony builds on the work of all previous participants.)
• Well-formedness of pp 1: these elements indeed encode incremental powers. (This verifies the good form of the new participant's contribution to the ceremony.)
• Update is non-erased: τ' ≠ 0. (This defends against attackers trying to undermine the system by erasing all past work of participants.)

The smart contract verifies the proof, and if it is correct, it updates the public parameters it stores. You can find more details about the mathematics and the reasoning behind it in the repository.

Calculating Gas Costs

The main challenge of running the setup on-chain is to make the trusted setup ceremony as efficient as possible. Ideally, the cost of submitting contributions should not exceed $50. (Larger projects may be able to subsidize Gas for contributors, in which case it is easier to imagine hundreds of participants each spending $100.) Below, we provide more details about the most expensive parts of the setup. Lower Gas costs will reduce contribution costs and allow for longer parameters (more powers of tau and larger SNARK circuits)!

Our setup is applicable to the BN254 elliptic curve (also known as BN256, BN128, and alt_bn128), which supports the following precompiled contracts on Ethereum:

ECADD allows adding two elliptic curve points, i.e., computing [α + β]1 from [α]1 and [β]1: Gas cost 150

ECMULT allows multiplying an elliptic curve point by a scalar, i.e., computing [a * α]1 from a and [α]1: Gas cost 6,000

ECPAIR allows checking the product of elliptic curve pairs, i.e., computing e([α1]1, [β1]2) * … * e([α1]1, [β1]2) = 1, equivalent to checking α1 * β1 + … + αk * βk = 0: Gas cost 34,000 * k + 45,000

If Ethereum can enable BLS12_381 (as suggested in EIP-2537), our setup contract could also be easily used for other curves.

Let’s estimate the Gas cost of updating the setup to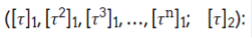

Verifying the proof's Gas cost. As mentioned, each participant updates the setup and submits a proof containing three components. The proof components 1 and 3—"knowledge of discrete logarithm" and "update is non-erased"—are very cheap to verify. The challenge lies in verifying component 2, "well-formedness of pp" 1 on-chain. It requires a large multi-scalar multiplication (MSM) and two pairings:

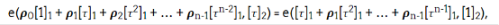
Where ρ0,…,?n-1 are pseudo-randomly sampled scalars. In terms of precompiled smart contracts, it requires:

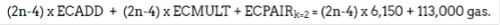
The Gas cost of storing data. Each participant will also update the on-chain storage as call data (68 gas per byte), totaling n * 64 * 68 gas. (For those familiar with elliptic curve cryptography, it is worth noting that based on our measurement for n = 256, storing compressed points will dominate the overall cost when decompressing.)

The estimated Gas costs are as follows:

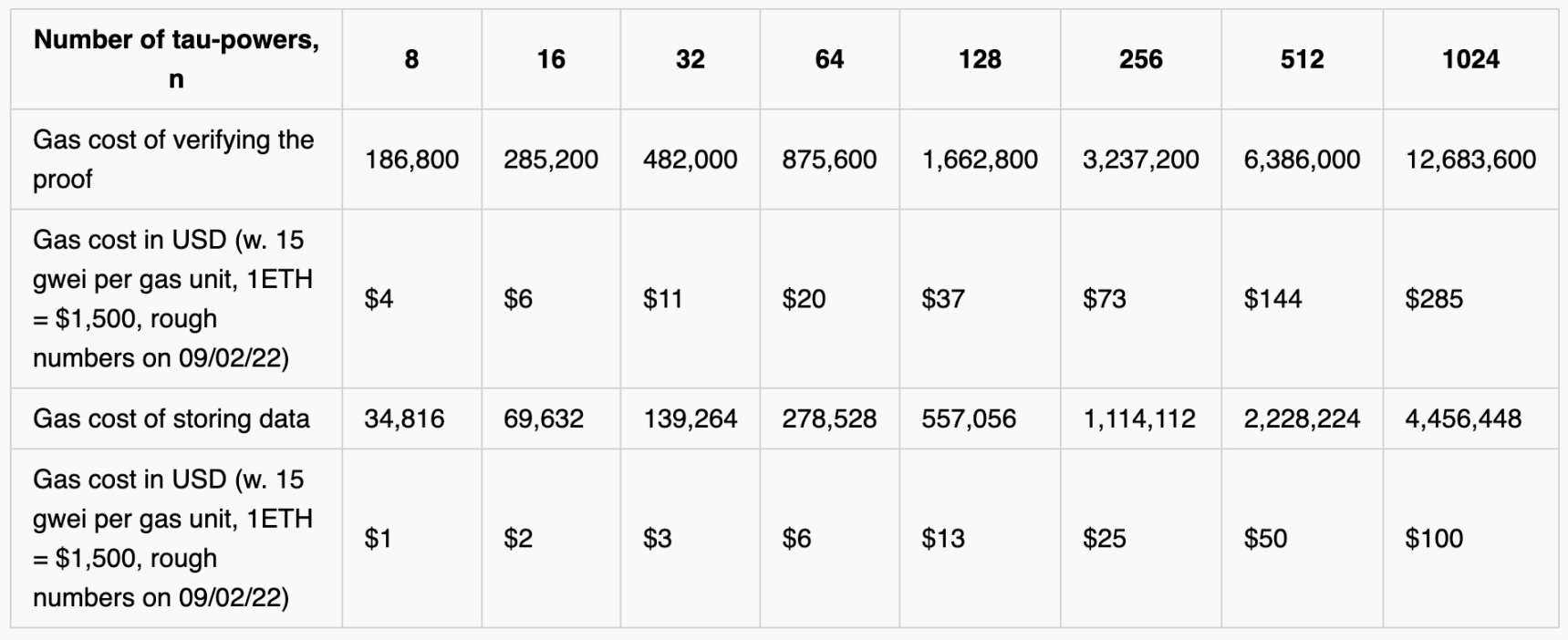
Of course, we are also exploring solutions to reduce Gas costs.

Open Source Library: evm-powers-of-tau

We have open-sourced the EVM-based powers-of-tau ceremony at github.com/a16z/evm-powers-of-tau. Using our strategy for the ceremony is both simple and transparent:

• Deploy the storage and verification protocol (protocol/KZG.sol)
• Participants read the ceremony parameters from previous transaction call data
• Participants locally generate a key and compute updated parameters
• Contributors generate their proofs: pi1, pi2
• Contributors submit the updated parameters to the smart contract deployed on the public blockchain via KZG.potUpdate()
• The smart contract verifies the validity of the update and recovers in case of incorrectly formatted submissions
• Multiple contributors can permanently execute steps 2-5, each step enhancing the security of the ceremony
• Whenever developers are confident in the quantity and quality of submissions, they can query the current parameters on the blockchain and use these values as cryptographic keys.

Our repository uses arkworks-rs to compute steps 2 and 3 (Rust computation can be found in src/potupdate.rs), but users may want to write their own. The entire end-to-end process of submitting updates can be found in the integration tests in tests/integrationtest.rs.

Note that we chose to use calldata to store the updated powers-of-tau parameters on-chain because it is several orders of magnitude cheaper than storage. Queries for this data based on ethers-rs can be found in src/query.rs.

Finally, proofs and detailed equations can be found in the technical report at techreport/main.pdf.

Future Work Plans

Before using this trusted setup ceremony in a production environment, we recommend conducting a comprehensive audit of the mathematical proofs and example implementations.

As implementation progresses, the transaction costs of updating the ceremony grow linearly with the size of the setup. For most applications (SNARKs, DAS), we hope to set n >= 256, with the current cost per update being $73.

We may be able to achieve sub-linear growth in verification costs through efficient updates computed by STARK proofs and vector commitments of the updated values. This structure would also eliminate the dependency on Ethereum L1 BN254 precompiles, allowing the use of the more popular BLS12-381 curve.

All ceremony strategies are the result of repeated trade-offs and testing. We believe this structure is reliable and has good verifiability and censorship resistance. However, similarly, until more work is completed to validate the soundness of our approach, using the scheme mentioned in this article directly still requires a high degree of caution.