Vitalik Buterin: How to Use zk-SNARKs Technology to Protect Privacy?

Author: Vitalik Buterin

Original Title: 《Some ways to use ZK-SNARKs for privacy》

Compiled by: Decentralized Finance Community

ZK-SNARKs are a powerful cryptographic tool that is becoming an increasingly important part of applications built both on and off the blockchain. However, they are complex, both in terms of how they work and how we use them.

This article will focus on how ZK-SNARKs fit into existing applications, what examples illustrate what they can and cannot do, and what general guidelines can be used to determine whether ZK-SNARKs are suitable for certain specific applications.

This article specifically focuses on the application of ZK-SNARKs in privacy protection.

What do ZK-SNARKs do?

Suppose there is a public input x, a private input w, and a (public) function f (x,w)→{True,False} that performs some verification on the inputs. Using ZK-SNARKs, you can prove that you know a w such that for some given f and x, f (x,w)=True, without revealing what w actually is. Additionally, the verifier can verify the proof much faster than they could compute f (x,w) themselves, even if they know w.

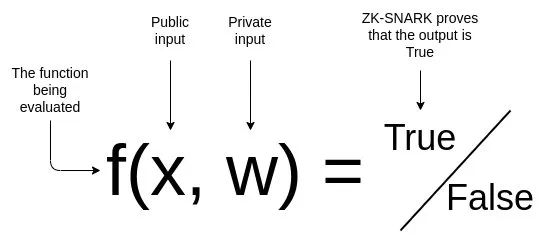
This endows ZK-SNARKs with two properties: privacy and scalability. As mentioned above, our examples in this article will focus on privacy.

Proof of Membership

Suppose you have an Ethereum wallet and you want to prove that this wallet is registered with a proof-of-humanity, without revealing which person is registered. We can describe this function mathematically:

• Private input (w): your address A, your address private key k
• Public input (x): the set of addresses of all verified proof-of-humanity profiles {H1…Hn}
• Verification function f (x,w)
• Interpret w as a pair (A,σ), with x as the list of valid profiles {H1…Hn}
• Verify that A is one of the addresses in {H1…Hn}
• Verify that privtoaddr (k) = A
• If both verifications pass, return True; if either verification fails, return False

The prover generates their address A and the associated key k, and provides w=(A,k) as the private input to f. They obtain the public input from the chain, which is the current set of verified proof-of-humanity profiles {H1…Hn}. They run the ZK-SNARK proof algorithm, which (assuming the inputs are correct) generates a proof. The prover sends the proof to the verifier and provides the block height at which they obtained the verified profile list.

The verifier also reads the chain to get the list {H1…Hn} at the height specified by the prover and checks the proof. If the check passes, the verifier believes that the prover has some verified proof-of-humanity document.

Before we continue discussing more complex examples, I strongly recommend reviewing the above example until you fully understand all its components.

Making Membership Proofs More Efficient

One drawback of the above proof system is that the verifier needs to know the entire profile set {H1…Hn}, which requires O(n) time to "input" this set of profiles into the ZK-SNARK mechanism.

We can solve this problem by using the on-chain Merkle root that contains all the profiles as the public input (this could simply be the state root). We add another private input, a Merkle proof M, proving that the prover's account A is in the relevant part of the tree.

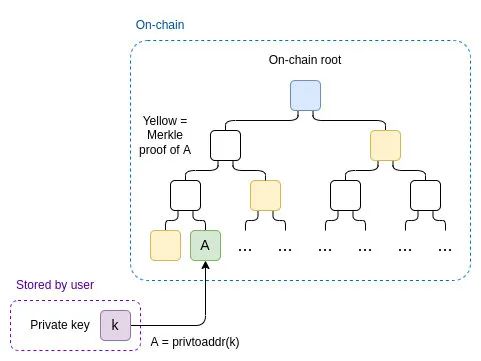
A very new and more efficient alternative for ZK proof of membership using Merkle proofs is Caulk. In the future, some of these use cases may migrate to solutions similar to Caulk.

ZK-SNARKs and Currency

Projects like Zcash and Tornado.cash allow us to have privacy-preserving currency. Now, you might think you can use the above "ZK proof of humanity," but it does not prove access to the proof-of-humanity profile; rather, it is used to prove access to the currency. Now we have a problem: we must solve both the privacy and double-spending issues. In other words, we should not spend the same currency twice.

We solve this as follows. Anyone who has currency has a private secret "s." They locally compute "leaf" L=hash (s,1), which is published on the chain and becomes part of the state, N=hash (s,2), which we call the nullifier. The state is stored in a Merkle tree.

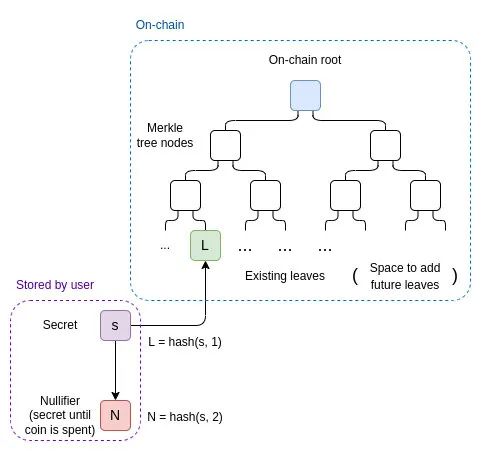
To spend a currency, the sender must create a ZK-SNARK where:

• The public input includes a nullifier N, the current or recent Merkle root R, and a new leaf L' (the purpose is for the recipient to have a secret s' and pass to the sender L' =hash (s',1))
• The private input includes a secret s, a leaf L, and a Merkle branch M
• The verification function checks:
• M is a valid Merkle branch proving that L is a leaf of the tree with root R, where R is the current state Merkle root
• hash (s,1)=L
• hash (s,2)=N

The transaction includes the nullifier N and the new leaf L'. We do not actually prove anything about L', but we "mix" it into the proof to prevent the transaction from being modified by a third party during the process.

To verify the transaction, the chain checks the ZK-SNARK and additionally checks whether N has been used in previous spending transactions. If the transaction is successful, N is added to the set of spent nullifiers so that it cannot be used again. L' is added to the Merkle tree.

Here we use zk-SNARKs to link two values, L (which appears on the chain when the currency is created) and N (which appears on the chain when the currency is consumed), without revealing which L is connected to which N. Only when you know the secret s that generated these two values can you discover the connection between L and N. Each created currency can only be used once (because for each L, there is only one corresponding valid N), but the currency used at a specific time is hidden.

This is also an important primitive that needs to be understood. Many of the mechanisms we describe below are based on this, although the purposes are different.

Currency with Arbitrary Balances

The above situation can be easily extended to currencies with arbitrary balances. We retain the concept of "currency," but each currency is attached to a (private) balance. A simple way to achieve this is to have each currency have chain storage, not just a leaf L, but also an encrypted balance.

Each transaction will consume two currencies and create two new currencies, adding two pairs (leaf, encrypted balance) to the state. ZK-SNARK will also check that the sum of the input balances equals the sum of the output balances, and that both output balances are non-negative.

ZK Anti-Denial of Service

An interesting anti-denial of service gadget. Suppose you have some on-chain identity, which is not easy to create; it could be a proof-of-humanity profile, or it could be 32 ETH validators, or it could simply be an account with a non-zero ETH balance. We can create a more DoS-resistant peer-to-peer network by only accepting messages that come with a proof that the message sender has a profile. Each profile will be allowed to send up to 1000 messages per hour, and if the sender cheats, their profile will be removed from the list. But how do we protect privacy?

First, the setup. Let k be the user's private key; A=privtoaddr (k) is the corresponding address. The list of valid addresses is public (for example, it is an on-chain registry). So far, this is similar to the proof-of-humanity example: you must prove you own the private key of an address, but cannot reveal which address it is. But here, we do not just want to prove you are on the list. We want a protocol that allows you to prove you are on the list while preventing you from making too many proofs.

We will divide time into several periods: each period lasts 3.6 seconds (so there are 1000 periods per hour). Our goal is to allow each user to send only one message per period; if a user sends two messages in the same period, they will be caught. To allow users to occasionally send burst messages, they can use the most recent periods, so if a user has 500 unused periods, they can use those periods to send 500 messages at once.

Protocol

We will start with a simple version: using a nullifier. The user generates a nullifier with N=hash (k,e), where k is their key and e is the period number, and publishes it along with the message m. ZK-SNARK again mixes hash (m), without verifying anything about m, thus binding the proof to a single message. If the user binds two proofs to two different messages using the same nullifier, they may be caught.

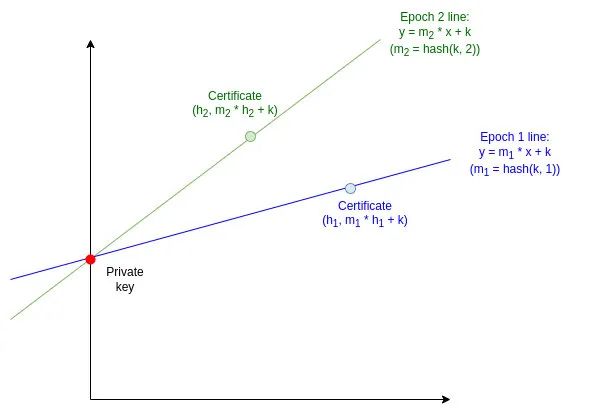
Now, we will move to a more complex version. In this case, the next protocol will expose their private key instead of simply proving whether someone has used the same period twice. Our core technique will rely on the "two points make a line" trick: if you show a point on a line, you reveal very little, but if you show two points on a line, you reveal the entire line.

For each period e, we take the line Le (x)=hash (k,e)∗x+k. The slope of the line is hash (k,e), and the y-intercept is k; both are not known to the public. To create a certificate for message m, the sender provides y=Le (hash (m))= hash (k,e)∗hash (m)+k, along with a ZK-SNARK proof that the computation of y is correct.

In summary, the ZK-SNARK is as follows:

Public Inputs:

• {A1…An}, the list of valid accounts
• M, the message for which the certificate is being verified
• E, the period number for the certificate
• Y, the evaluation of the line function

Private Inputs:

• K, your private key

Verification Function:

• Check if privtoaddr (k) is in {A1…An}
• Check if y=hash (k,e)∗hash (m)+k

But what if someone uses a period twice? This means they revealed two values m1 and m2 along with the corresponding certificate values y1=hash (k,e)∗hash (m1)+k and y2=hash (k,e)∗hash (m2)+k. We can use these two points to recover the line, thus revealing the y-intercept (which is the private key):

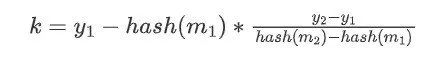
Therefore, if someone reuses a period, they will leak their private key for everyone to see. Depending on the situation, this could mean stolen funds, or simply broadcasting the private key and including it in a smart contract, at which point the corresponding address will be removed from the collection.

A feasible off-chain anonymous anti-denial of service system, applicable to blockchain peer-to-peer networks, chat applications, and other systems, does not require any proof of work. The RLN project is essentially building this idea, albeit with some modifications (that is, they use both nullifiers and the two-point line technique, making it easier to capture the double-use of a period).

The Negative Reputation of ZK

Suppose we want to establish 0chan, a completely anonymous online forum like 4chan (where you don't even have a permanent name), but with a reputation system to encourage higher quality content. This could be a system where some auditing DAOs can flag posts that violate system rules and establish a three-strike mechanism.

The reputation system can support both positive and negative reputations; however, supporting negative reputation requires additional infrastructure that requires users to consider all reputation information in the proof, even if it is negative. We will focus on this more challenging use case, which is similar to what Unirep Social is implementing.

Linking Posts: The Basics

Anyone can post by publishing a message on-chain that includes the post and a ZK-SNARK to prove (i) you have some scarce external identity that authorizes you to create an account, or (ii) you have posted some specific posts. Specifically, the ZK-SNARK is as follows:

• Public Inputs:
• nullifier N
• The most recent blockchain state root R
• Post content (mixed into the proof, binding it to the post, but we do not perform any computation)

Private Inputs:

• Your private key k
• An external identity (address A), or the nullifier Nprev used in the previous post
• A Merkle proof M proving that A or Nprev is included on-chain
• Your i-th post published with this account

Verification Function:

• Check that M is a valid Merkle branch proving (A or Nprev, depending on the provider) is a leaf of the tree with root R
• Check that N=enc (i,k), where enc is an encryption function (e.g., AES)
• If i=0, check that A=privtoaddr (k), otherwise check that Nprev=enc (i−1,k)

In addition to verifying the proof, the chain also checks two aspects: (i) R is indeed a recent state root, and (ii) the nullifier N has not been used yet. So far, this is similar to the privacy-preserving currency introduced earlier, but we have added a process for "minting" new accounts, and we have removed the ability to "send" your account to a different key—instead, all nullifiers are generated using the original key.

We use enc here to make the nullifier reversible rather than hash: if you have k, you can decrypt any specific nullifier on-chain, and if the result is a valid index rather than random garbage (for example, we can just check dec (N)<264), you will know that the nullifier was generated using k.

Adding Reputation

In this scheme, reputation is on-chain and explicit: some smart contracts have a method addReputation that takes (i) the nullifier accompanying the post and (ii) the number of reputation units to add or subtract as inputs.

We extend the on-chain data stored for each post: we store {N,h¯,u¯} instead of just storing the nullifier N, where:

• h¯=hash (h,r) where h is the block height of the state root referenced in the proof
• u¯=hash (u,r) where u is the account's reputation score (new accounts start at 0)

Here, R is just a random value, and adding it is to prevent h and u from being discovered through forced search (in cryptographic terms, adding R makes the hash a hidden commitment).

Suppose the post uses root R and stores {N,h¯,u¯}. In the proof, it links to previous posts, storing the data {Nprev,h¯prev,u¯prev}. The proof of the post also needs to traverse all reputation entries published between hprev and h. For each nullifier N, the verification function will use the user's key k to decrypt N, and if the decrypted output is a valid index, it will apply the reputation update. If the total sum of all reputation updates is δ, then the final proof will be u=uprev+δ.

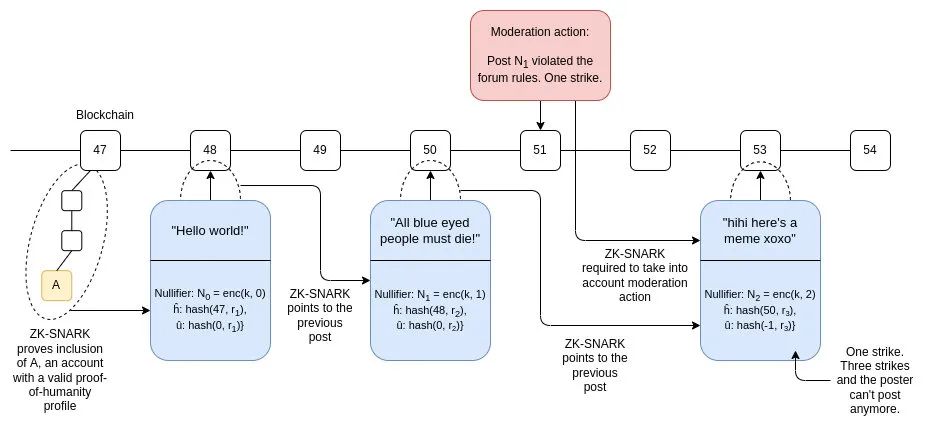
If we want a "three-strike" rule, the ZK-SNARK will also check if u>−3. If we want a rule that if the post's rep≥100, then the post can receive a special "high reputation post" identifier.

To improve the scalability of the scheme, we can divide it into two categories of messages: posts and RCAs. A post will be off-chain, although it needs to point to the RCAs made in the past week. RCAs will be on-chain, and they will traverse all reputation updates since the last RCA made by that publisher. In this way, the on-chain load is reduced to one transaction per post per week plus one transaction per reputation message.

Holding Centralized Parties Accountable

Sometimes, you need to build a scheme with some centralized "operator." There can be many reasons behind this: sometimes for scalability, sometimes for privacy (specifically, for the privacy of the data held by the operator).

For example, MACI enforces a voting system that requires voters to submit their votes on-chain, encrypted to a key held by a centralized operator. The operator will decrypt all the votes on-chain, count them, and display the final results while using ZK-SNARKs to prove that everything they did was correct. This additional complexity is necessary to ensure strong privacy (called enforced resistance): users cannot prove to others how they voted, even if they want to.

Thanks to blockchain and ZK-SNARKs, we can keep our trust in the operator at a very low level. A malicious operator could still break enforced resistance, but because the voting is published on-chain, the operator cannot cheat by censoring votes, and because the operator must provide ZK-SNARKs, they cannot cheat by incorrectly calculating the results.

Combining ZK-SNARKs with MPC

A more advanced use of ZK-SNARKs involves proving computations where inputs are distributed among two or more parties, and we do not want any party to learn the inputs of the others. In the case of two parties, you can satisfy privacy requirements using garbled circuits, while in the case of N parties, you can use more complex multiparty computation protocols to satisfy privacy requirements. ZK-SNARKs can be combined with these protocols for verifiable multiparty computation.

This can enable more advanced reputation systems where multiple participants can perform joint computations on their private inputs. The mathematical computations to effectively achieve this are still at a relatively early stage.

What Can’t We Set as Private?

ZK-SNARKs are very effective for creating systems where users have private states. However, ZK-SNARKs cannot maintain private states that no one knows about. To prove a piece of information, the prover must know that information in plaintext.

Uniswap is an example that is not easy to privatize. In Uniswap, there is a logically central "thing," which is the liquidity provider account, that does not belong to anyone, and every transaction on Uniswap is a transaction with the liquidity provider account. You cannot hide the state of the liquidity provider account because someone must hold that state in plaintext to prove it, and every transaction requires their active participation.

You could create a centralized, secure, private Uniswap using ZK-SNARK's garbled circuits, but it is unclear whether the benefits of doing so would outweigh the costs of executing it. It may not even provide any real benefits: contracts need to be able to tell users what the price of assets is, and block-by-block price changes can inform users about trading activity.

Blockchains can globalize state information, and ZK-SNARKs can privatize state information, but we really do not have any good methods to globalize state information while achieving privatization.

Putting the Primitives Together

In the subsections above, we have seen examples of some powerful and useful tools that can also serve as building blocks for other applications. For instance, nullifiers are crucial for currency, and they are now reappearing in other use cases.

The "enforced linking" technique used in the negative reputation section has a very wide applicability. It is very effective for many applications where users' "profiles" change in complex ways over time, and you want to enforce users to comply with the system's rules while protecting privacy. Users could even be required to represent their internal "state" with a complete private Merkle tree. The "commitment pool" gadget proposed in this article can be constructed using ZK-SNARKs. If certain applications cannot be fully on-chain and must have a centralized operator, the exact same techniques can also be used to keep the operator honest.

ZK-SNARKs are a very powerful tool that combines the benefits of accountability and privacy. While they do have their limitations, in some cases, clever application design can work around these limitations. I hope to see more applications using ZK-SNARKs and ultimately building applications that combine ZK-SNARKs with other forms of cryptography in the coming years.