Lyra: Friendlier Risk Management and Precise Pricing Options
Author: Loners Liu
1. The Rise of On-Chain Derivatives and the Issues with Decentralized Options
On September 22, according to CoinMarketCap data, the decentralized derivatives protocol dYdX had a 24-hour trading volume of $2.077 billion, surpassing Uniswap V3's 24-hour trading volume of $1.991 billion, ranking first in the DEX leaderboard.
The rapid growth in dYdX's trading volume has made people realize that features such as security, decentralization, transparency, censorship resistance, and permissionless access are attracting more and more traders to the decentralized derivatives market. After experiencing exponential growth and maturation in the perpetual contract market, it is believed that the market's desire for options trading will also be unleashed in cryptocurrencies.
In fact, centralized cryptocurrency options already have sufficient liquidity, and some structured products (packaged options strategies provided by dealers to clients) have begun to emerge.
Currently, the first problem faced by DeFi options products is the liquidity issue. Accompanied by impermanent loss and high-risk combinations, there is little appeal for LPs, resulting in consistently low liquidity. Protocols with some liquidity offer extremely high prices to avoid the complexities of options pricing, and these uncompetitive prices naturally lead to low trading volumes.
Additionally, the second unavoidable problem faced by DeFi options products is the pricing issue. The traditional options market uses the Black-Scholes model as its pricing formula. It was after the introduction of the Black-Scholes model that options sellers realized they could dynamically replicate options risk through delta hedging (i.e., their exposure to changes in the underlying market price over time). DeFi options products also often adopt this method. However, the implied volatility in the model is the difficulty of this pricing method. Hegic's implied volatility (IV) is manually extracted from Skew, and automation will be implemented when Chainlink's implied volatility oracle becomes available.
2. Introduction to Lyra's Options and the Black-Scholes Pricing Model
Lyra is a layer-2 options protocol on Synthetix. It is well-known that Synthetix has been a strong supporter of Ethereum and the Layer 2 scaling solution Optimism, participating in Optimism's testnet last year, launching the SNX reward program, and providing the Teleportr cross-bridge service for lower-cost transfers of ETH to the Optimism layer-2 network. Therefore, as a member of the Synthetix ecosystem, Lyra is naturally deployed on Optimism.
In addition to being compatible with Ethereum EVM, Optimistic Rollups can provide a faster general environment with multiple applications, which is a basic requirement for Lyra, as it needs to combine with external markets to hedge risks. Another major benefit of being built on layer-2 is the reduction in transaction costs, with transfer costs on Optimism being half of that on layer-1, and the fees for calling complex contracts being one-tenth, making relatively low fees more likely to stimulate users' trading desires.
Lyra is also the first options AMM that combines with other DeFi projects to automatically price and hedge risks for LPs. The order book model in DeFi has long provided liquidity for various options, but for relatively less popular assets (i.e., any non-BTC/ETH assets), the iterative AMM model converges to ultimately provide flexibility for LPs while retaining instant liquidity, which is also the reason why AMMs have brought explosive growth to the entire DeFi industry.
Of course, options can theoretically also serve as a form of leverage. As the saying goes, good decisions carry the attribute of "asymmetric returns." This means that the problems and risks arising from incorrect decisions have a lower limit, while the gains from correct decisions have no upper limit, and this statement naturally applies to options trading.
Let’s look at a simple example: Suppose Alice pays $5 to purchase a call option for a token ABC with a strike price of $110, expiring on June 30. The right she purchases is to pay $110 for one ABC token on or before June 30. The $5 she paid is called the premium. On June 30, if the price of ABC rises to $130, compared to the $30 (+30%) profit from simply holding ABC, the option allows her to buy the token at $110 and then sell it at $130, yielding a profit of $15. Considering the $5 cost of the option, her profit is $20 - $5 = $15, resulting in a 300% return on investment.
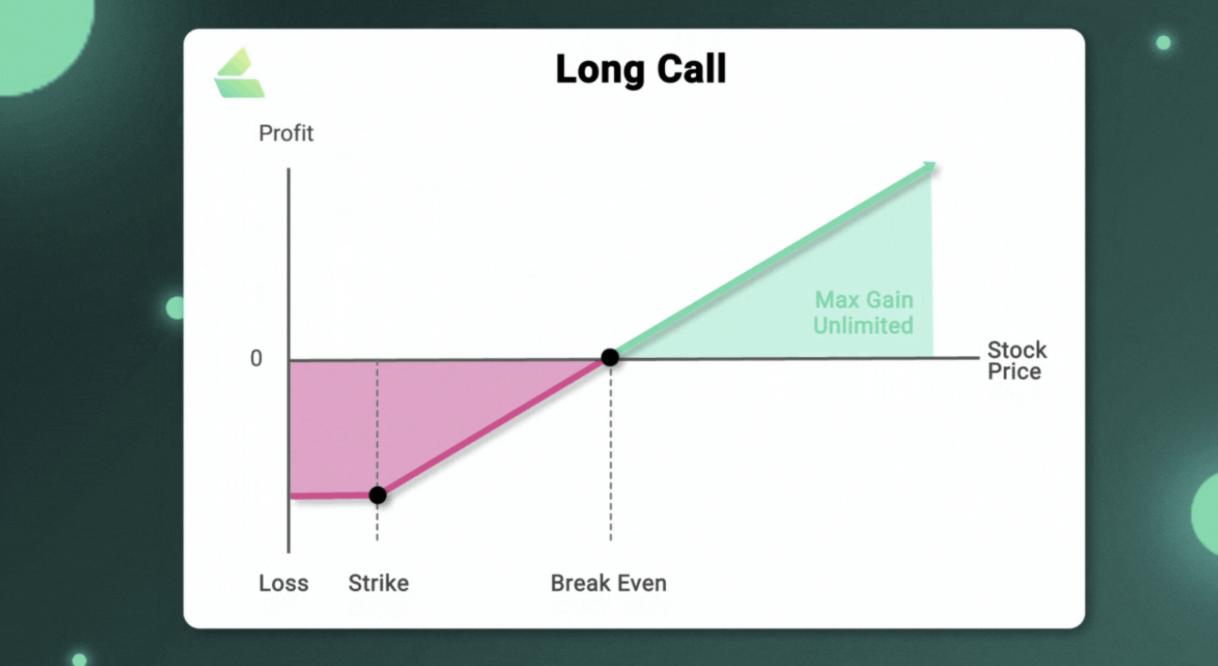
In the above scenario, Alice's return rate is 10 times that of simply purchasing ABC spot, so in options trading, your loss is your option premium (or insurance premium), but because of the asset's rise, the potential gains can be enormous, perfectly illustrating that the problems and risks arising from incorrect decisions have a lower limit, while the gains from correct decisions have no upper limit.
Of course, all of this is predicated on the options protocol having a complete pricing mechanism. Lyra uses dynamic volatility inputs and the Black-Scholes model to price the entire options. Other options protocols use static implied volatility or other less accurate methods for pricing options.
Like most centralized exchanges, Lyra adopts European options, granting traders the right to buy/sell call/put options (long) on the underlying asset at a certain price on a specific date, with the final result denoted as W. This model uses the following five key parameters:
Time to expiration (T-t), where t is the current time
Risk-free interest rate (r)
Current price of the underlying asset t(St)
Strike price of the option (K)
Implied annualized volatility (IV) of the underlying asset
Lyra uses market demand and supply to plot the implied volatility surface for each expiration date, and then inputs this surface into the Black-Scholes pricing model to determine the prices of all listed options, providing efficient pricing for traders.
Lyra's Black-Scholes smart contract implements a mathematical formula related to calculating option prices (using the Black-Scholes pricing model). It not only includes core mathematical functions (exp, ln, sqrt, std Normal, and std NormalCDF) but also implements specific functions of Black-Scholes (d1d2, option Prices, delta, vega). In addition, it also implements a standardized Vega function as described in the white paper (std Vega).
3. Delta and Vega Risk Management Strategies in the Lyra Protocol
As a hedging tool, options provide DeFi traders with strategies to reduce risk. To achieve this vision, it is necessary to establish the required derivatives infrastructure and risk management tools to protect DeFi users. Considering the high risks in options trading, without active risk management, liquidity providers are prone to impermanent loss. Lyra adopts a strategy of dynamically adjusting Delta and Vega to hedge LPs' risks.
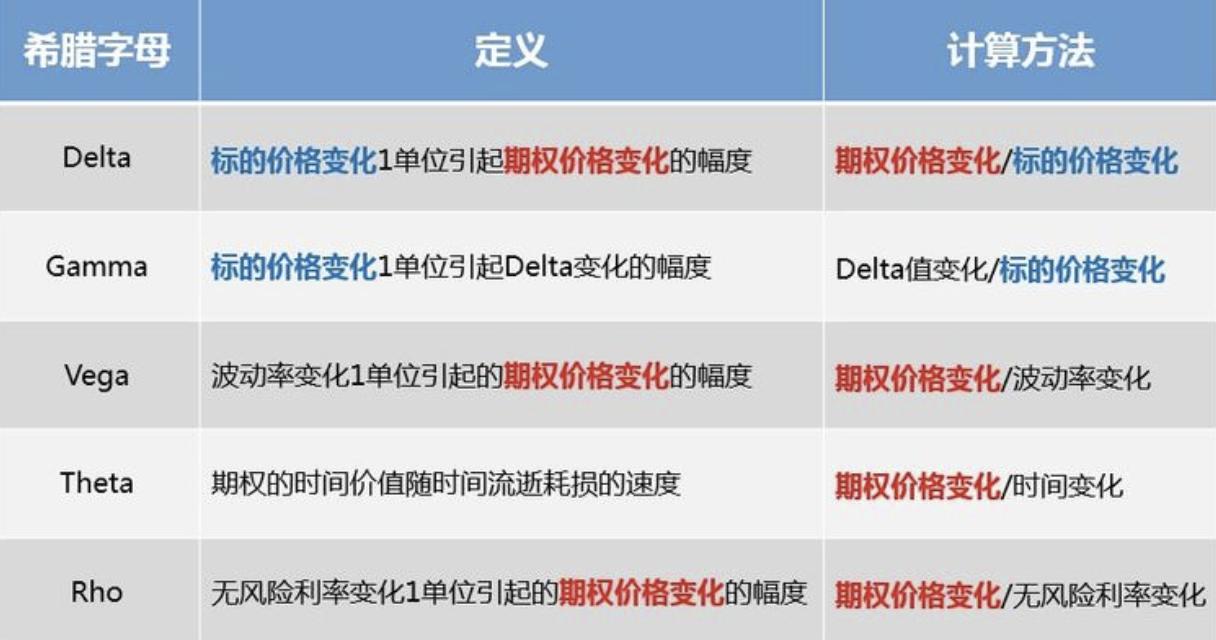
In options, Delta, Vega, Gamma, Theta, and Rho can reflect the sensitivity to current prices, where Gamma, Theta, and Rho have a risk impact that is secondary to Delta and Vega. Since Gamma and Theta risks can be dynamically adjusted based on Delta and Vega, Rho risk is usually much smaller than other risks because the risk-free rate tends to be quite stable. Therefore, the following discussion focuses on how to manage and hedge Delta and Vega risks in the Lyra protocol.
Delta Hedging Strategy
Delta is the most important sensitivity indicator for options, defined as Delta = change in option price / change in spot price, meaning the extent of change in the option price when the spot fluctuates by one unit.
In traditional finance, investors often construct portfolios containing options through delta-neutral strategies. Lyra's AMM actively hedges liquidity providers' Delta by trading the underlying asset (automatically long/shorting the underlying asset through Synthetix), controlling the risks of liquidity providers and bringing the overall Delta back to neutral.
The steps for Delta hedging in Lyra are as follows:
Calculate the Delta for each option product, with detailed numbers displayed on the trading page.
Obtain the net position for each AMM.
Multiply the net position of each AMM by the corresponding Delta.
Calculate the sum of the above products for each category of products to obtain the net Delta.
Buy (when Delta is negative) or sell (when Delta is positive) an equivalent amount of tokens to bring the underlying asset back to Delta neutral.
For example, if there are two products with Delta of 0.5 and 0.3, and the AMM is short 10 ETH and long 3 ETH, then net Delta = 0.5 x (-10) + 0.3 x 6 = -3, which means the AMM is short 3 ETH and needs to buy 3 ETH from an external exchange to return to Delta neutral.
Dynamic Adjustment of Vega Risk
The goal of options market makers is to find an implied volatility (LV) value where demand roughly equals supply. In this case, the AMM can collect trading fees without bearing risk, as it is buying and selling the same number of options.
The prices of options trading will revolve around the theoretical values of Black-Scholes, but to reduce the risks for liquidity providers, Lyra generates asymmetric price differences based on whether the trade reduces or increases the total risk exposure (charging extra fees for trades that increase the liquidity pool's Vega risk). Trades that increase the liquidity pool's risk exposure will be suppressed, while trades that reduce risk will be promoted. This fee is proportional to the size of the current risk of the AMM (i.e., as the pool bears more risk, the fees also increase).
The specific fee structure is as follows:
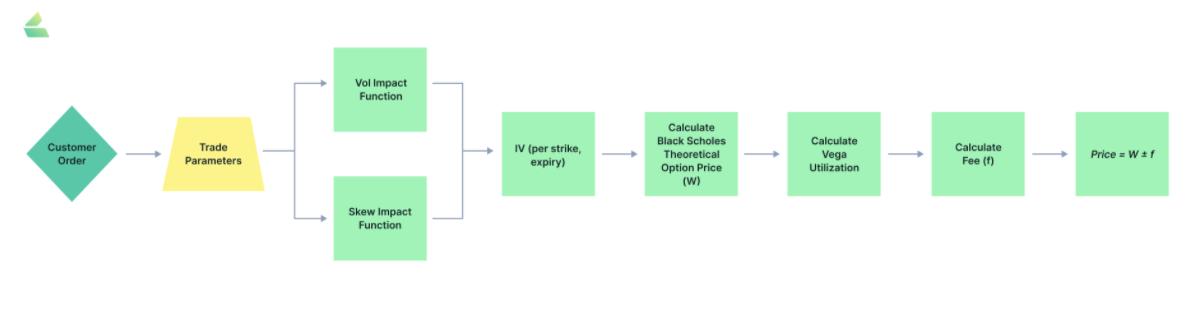
The final price of an option F = W ± f, where W is the result derived from the implied volatility input into the Black-Scholes model, and f depends on the following formula:

VU vega utilization represents the sensitivity of the option to volatility. According to the official documentation, when a trade increases the total risk exposure, it is 1; otherwise, it is 0. B here can be understood as the impact on increasing risk. Of course, the A, B, and C in the formula are initially set by the project team and later governed by the community.
For a simple example, if a call option priced at $100 according to Black-Scholes has a net short position of 500 Vega in the AMM, the AMM might be willing to buy that call option at $95 while continuing to sell it at $110. The additional Vega increases the buyer's price by $5.
Additionally, Lyra can gauge the Delta/Vega risk of the option position by examining whether our asset price rises during the trade with a happy or sad expression, which adds a fun element.
4. Summary Analysis of the Lyra Protocol
Lyra's overall mechanism was designed in March this year, with engineering basically completed in April and third-party audits finished in May. In July, it launched on the Ethereum testnet Kovan version of the scaling solution Optimism, and on August 25, it officially announced its launch on the Ethereum layer-2 scaling solution Optimism mainnet, with the V2 version expected to launch in the fourth quarter according to the official roadmap.
Recently, Lyra has proposed LEAP-3, which will launch the first LYRA liquidity incentive pool on the Optimism mainnet, distributing LYRA rewards to users providing liquidity to Uniswap sUSD / Dai and ETH Market Pool.
From Uniswap V3's sUSD/DAI liquidity pool, which ranks first in volume on Optimism (approximately $12 million), we can see the effect of this liquidity incentive. However, in the long term, since all trades require sUSD as the underlying asset, and sUSD must be minted by SNX stakers at a 750% c-ratio, it is necessary to gradually increase the supply of SNX on Optimism to drive the growth of Lyra and Thales trading data to maintain LP returns.
At the same time, charging excessively high fees for trades that increase Vega risk exposure is also detrimental to users conducting hedging trades. While it somewhat protects LP interests, it also reduces the potential earnings of some traders.
In summary, Lyra calculates and hedges risks for LPs, allowing AMMs to trade options at competitive prices while managing Delta and Vega risks effectively, bringing a new trading paradigm to DeFi and derivatives. However, it is important to note that while Lyra's AMM is a significant improvement available on-chain, it does not completely hedge LPs and can only undergo repeated market tests and pressure tests, continuously modifying to iterate better products.











