3.1 Secret Engine

认识到每个零知识证明系统都由两部分组成：一是算法，二是多项式承诺方案。将程序转化为零知识证明(ZKP)的初始阶段涉及到算法。这个过程通过在这些多项式之间建立特定的条件来阐明它们之间的关系。

我们的零知识证明系统是基于标准 PlonK 配方实现的，具有高度定制的 gates，主要包括：

• 小工具：支持游戏电路开发中使用的各种小工具，包括基本算术电路、哈希、ECC、zkshuffle、zkmatchmaking等。 我们建议访问我们的 GitHub 存储库以获取有关这些小工具的更多信息。

• 链上验证器：为证明者和验证者优化了PLONK/ZKVM，同时支持所有EVM链的通用可靠性验证器。

• 应用程序特定的 Plonk：使用应用程序特定的 Plonk 作为基本方案ZK证明，用我们的SDK提供的各种小工具来编写特定的游戏电路。 同时我们还提供不同虚拟机（EVM/WASM/...）上的验证合约，可以运行在不同的区块链系统中，实现链下证明和链上验证。

接下来，我们将介绍两个重要的组件，由Secret Engine孵化的zkshuffle和zkmatchmaking。

3.1.1 ZK shuffle SDK

3.1.1.1 介绍

扑克游戏是一种备受欢迎的纸牌游戏。在现实生活中,游戏各方可以相互监督，以确保游戏的公平性。随着计算机网络的快速发展,通过网络连接的玩家也有了参与扑克游戏的机会，尽管如此，网络环境下如何确保游戏的顺利进行和公平性却是一个不小的挑战，这也是心理扑克协议所要解决的问题。

心理扑克是一种基于密码学原理构造的扑克游戏，自1979年Shamir、Rivest和Adleman提出了第一个心理扑克协议【15】以来，人们就开始研究心理扑克游戏的可行性。心理扑克与普通扑克玩法类似,主要区别在于心理扑克是在没有物理卡牌的网络环境中进行，且所有玩家默认是不诚实的，即存在作弊行为。第一个心理扑克协议是一个两方的扑克协议，该协议已经被证明存在安全漏洞。根据文献【16】，一场公平的心理扑克必须满足以下属性：

1. 唯一性：在传统扑克游戏中，通过明示卡牌以验证没有重复的卡牌。心理扑克协议应保证同样的特性。

2. 随机分布：在传统扑克游戏中，一名玩家进行洗牌，其他玩家可以实时观察，这意味着洗牌的玩家无法控制最终的洗牌结果。

3. 保密性：任何时候，如果牌堆是面朝下的，就不应该透露关于牌堆中任何卡牌的信息。此外，当玩家抽取一张卡牌时，其他玩家是不能够获取关于该牌的任何信息。

4. 没有可信第三方：依赖可信第三方是不行的，因为任何人都可以被收买，没有绝对可信的第三方。

1987年，Crépeau提出第一个安全的心理扑克协议【17】。此后,心理扑克协议方案开始涌现，但很大部分心理扑克协议的研究是基于TTP的，因为学术界广泛认为采用TTP是解决心理扑克协议公平性的一个有效办法。然而扑克作为一种娱乐、休闲游戏，很多场景并不存在第三方，也很难确保第三方可信，特别是在涉及区块链技术的情况下，通常不存在一个可信第三方，因此如何在无PPT的条件下实现公平的心理扑克协议具有重要的意义。Barnett-Smart协议【18】于2003年提出，它提供了两种解决方案，分别基于ElGamal和Pailler加密系统，但Pailler加密方案存在一个安全上限，即假设合谋人数不超过(N-1)/2 。随后，Castellà-Roca协议【19】提出,其采用了不同的加密方案,shuffle过程也比Barnett-Smart协议要快。

心理扑克协议开销主要集中在shuffle部分，但在今天零知识证明算法取得了快速的发展，如geometry【20】【21】指出，shuffle过程已经不再是一个瓶颈，并且geometry认为Barnett-Smart协议将完整的纸牌游戏协议需要划分成多个安全子协议：生成卡牌、masking、re-masking、shuffle等等，这些步骤可以轻松实现即插即用，其安全性假设也基于Decisional Diffie-Hellman。因此,我们的mental poker协议主要借鉴Barnett-Smart协议，但同时也考虑到在对一套扑克牌进行zkShuffle涉及到大量椭圆曲线运算，其电路规模必然相当庞大。为了解决这个问题，我们重新设计一种zkshuffle友好的TurboPlonk【22】算法，显著降低了电路门的规模。

3.1.1.2 基本概念

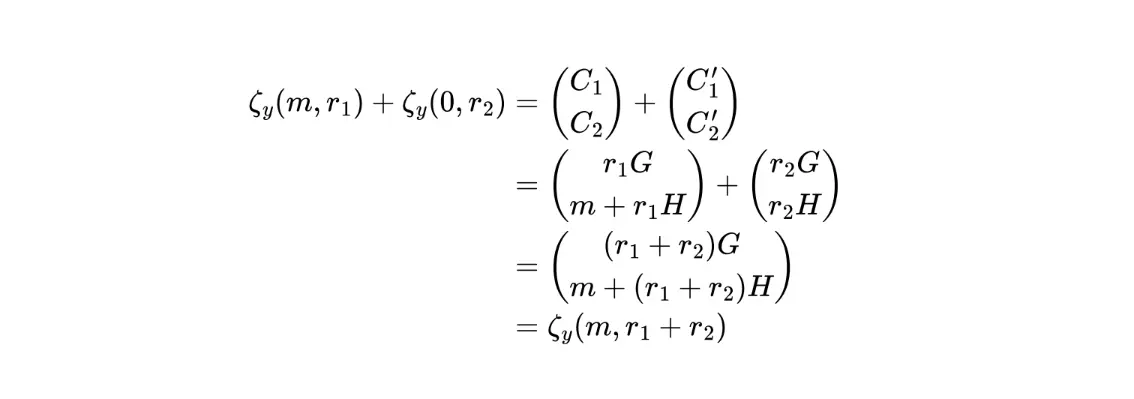
注：n-out-of-n threshold EIGamal encryption【23】

3.1.1.3 心理扑克协议

Mental poker 协议不是一个协议，而是包括了一组子协议,每个子协议负责一个行为。

• Key Generation:

• 为每一个玩家生成公私钥对
• 聚合所有玩家的公钥以生成一个公钥

• Masking:

• Masking函数是在聚合公钥下的一种ElGamal加密函数

• Shuffle and Re-masking:

• 执行洗牌操作以达到随机化卡牌的目的
• 对shuffle之后的卡牌再次进行mask

• Unmask:

• 解码卡牌以获取真实的卡牌信息

Key Generation protocol

Masking protocol

Re-Masking protocol

Shuffle argument

Unmask protocol

3.1.1.4 洗牌友好 PLONK 算法

Shuffle 协议主要包括两部分：1)对卡牌进行置换；2)对卡牌进行re-masking；其中 re-masking 操作涉及椭圆曲线运算，具体包括 1 个 Constant-base scalar multiplication、1 个 Non-constant-base scalar multiplication 和 2 个 curve addition，如果使用非优化TurboPlonk定制门(customized gates)来编写算术电路，对一张卡牌的re-masking的电路门数为596+1622+2=2220，那么对一套完整的牌组(52张)来说，电路门数将高达115440，这还不包括置换相关的电路。因此，如果采用非优化的TurboPlonk来编写算术电路，其shuffle时间将会非常漫长。为了解决这个问题，我们重新改造了TurboPlonk使其对shuffle运算友好，经过验证，对一个re-masking操作只需要 85 gates。

注：bowe hopwood【24】

3.1.1.5 链上验证

此外，在我们实践中，我们还遇到链上验证gas费高的问题，这里将主要和大家分享我们优化心得。

Verify reveal 解密一张卡牌，需要其它玩家提供相应的开牌信息，同时提供一个证明，用于验证开牌的正确性。现有Geometry的现实【25】基于chaum pedersen协议构造了一个开牌证明，我们知道chaum pedersen需要点乘运算，点乘操作是非常昂贵，主要因为目前以太坊不支持Baby Jubjub这条曲线的预编译合约，根据测试结果，基于Geometry实现下，验证开牌证明的gas费高达7629888，这显然是不可接受的。

考虑到 Baby Jubjub 是 BN254 的内嵌曲线，我们可以使用Snark进行开牌证明，根据gas的分析【26】，使用Groth16进行开牌证明的链上验证开销仅为约200k，这几乎比原生验证方式下降了30倍。相比于原生的验证方式，这似乎是一个非常不错的选择，开牌circuit如下：

未来，我们进行proof 聚合来更大程度的节省gas。

Verify shuffle 在德州扑克游戏中，我们需要将洗牌后的结果存储在链上，这不仅作为当前的shuffle结果，也用于后续shuffle circuit的公开输入。然而，一副扑克牌有52张，共计208个uint256类型数据，其链上存储成本昂贵。

我们的方案是只在链上存储部分扑克牌数据，具体来说，我们只需要存储2n+5张卡牌，其中n为玩家数量。考虑到我们的游戏最大同时支持6个玩家，因此最多只会用到17张牌。这意味着我们最终只需要在链上存储17张卡牌，节省了2/3存储开销。

尽管我们最终只需要在链上存储17张牌，但前文提到链上存储的另一个目的是，这些牌也将作为后续shuffle circuit的公开输入。因此如果只存储17张牌，就无法验证shuffle的正确性。为了解决这个问题，我们Shuffle电路会额外输出一个完整扑克牌的哈希值，存储在链上。在验证zkShuffle时，会作为电路的public input，从而保证了shuffle的正确性。

3.1.2 ZK matchmaking SDK

Matchmaking是一种旨在通过根据玩家水平进行游戏匹配的机制，以确保玩家在游戏中能够与实力相当的对手展开对战，从而提供公平且有趣的游戏体验。Matchmaking的核心目标可概括为以下两方面：

• 公平对抗：提供实力相当的玩家对抗，以使双方获胜的概率都尽可能倾向于50%。

• 不可预测性：匹配过程不可预测，即最终对战的选手不可预测。

整体流程

1. 申请成为 Prover 时，需向合约承诺一个种子，这个种子只有 Prover 知晓

2. 玩家发送加入游戏请求

3. 排序器接收到请求后，根据分级策略进行排序，然后将生成的队列分别发送给合约和证明者

4. Prover 基于 zkSnark 对不同队列进行随机匹配，匹配的结果依赖于 Prover 承诺的种子、输入的队列，以及链上随机数(确定的，但不可预测的)，然后将匹配的结果和 proof 发送给合约

5. 合约进行链上验证，如果验证通过，玩家根据匹配结果进入游戏

在区块链上，我们可以轻松获取像 block hash 那样的链上随机数，但它会受到矿工和验证者的区块扣留攻击，导致像 block hash 那样的链上随机数不是十分安全，以至于 Matchmaking 的不可预测性也会受到挑战。可验证随机函数 VRF 是一种具有验证性质的随机数生成器，能够生成统计上均匀不可预测的随机输出，并且其输出是可验证的，这为我们链上随机数提供了一种很好的解决方案。让我们简单了解下 VRF 的原理吧，其输入一个seed，输出一个随机数。

除了链上随机数，不可预测性也依赖于 Prover 承诺的种子，我们会构建惩罚机制来防止 Prover 随意泄漏随机数。

参考文献 ：

【15】A. Shamir, R. L. Rivest and L. M. Adleman, Mental poker, Technical report LCS/TM-125, Massachusetts Institute of Technology, April 1979.
【16】Crépeau C. A secure poker protocol that minimizes the effect of player coalitions, in: Conference on the Theory and Application of Cryptographic Techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 1985: 73–86.
【17】C. Crepeau, A zero-knowledge poker protocol that achieves confidentiality of the players’ strategy or how to achieve an electronic poker face, in: Advances in Cryptology – Crypto 086, Lecture Notes in Computer Science 263, Springer-Verlag, Berlin (1987), 239–247.
【18】A. Barnett and N. Smart, Mental poker revisited, in: Cryptography and Coding, Lecture Notes in Computational Science 2898, Springer-Verlag, Berlin (2003), 370–383.
【19】J. Castellà-Roca, Contributions to mental poker, Ph.D. Thesis, Autonomous University of Barcelona, Doctoral Programme in Computer Science and Artificial Intelligence, 2005.
【20】N Mohnblatt, A Novakovic and K Gurkan, Mental Poker in the Age of SNARKs - Part 1,
https://geometry.xyz/notebook/mental-poker-in-the-age-of-snarks-part-1 
【21】N Mohnblatt, A Novakovic and K Gurkan, Mental Poker in the Age of SNARKs - Part 1,
https://geometry.xyz/notebook/mental-poker-in-the-age-of-snarks-part-2
【22】Gabizon A, Williamson Z J. The turbo-plonk program syntax for specifying snark programs, in: ZKProof Workshop. 2020, 3.
【23】Desmedt Y. Threshold cryptosystems, in: International Workshop on the Theory and Application of Cryptographic Techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 1992: 1–14.
【24】https://github.com/arkworks-rs/crypto-primitives/tree/main/crypto-primitives/src/crh/bowe_hopwood.

【25】https://github.com/geometryxyz/mental-poker/blob/main/barnett-smart-card-protocol/src/discrete_log_cards/mod.rs#L320.

【26】Todd Norton, Groth16 Verification Gas cost,https://hackmd.io/@nebra-one/ByoMB8Zf