Uniswap v3 数学洞察：期权如何与头寸结合

AntalphaLabs

2023-11-29 22:00:50

解析 Uniswap v3 机制与投资策略。

分享至

微信扫码

撰文：ck.eth

编译：Lylia， Antalpha Labs

原系列共有六部分，此为第五部分，该篇继续介绍期权如何与头寸结合，需要对该系列之前所述的头寸策略有一定了解。为了让更多人可以访问和了解关于 Uniswap V3 的有用信息，我们翻译了系列文章，让中文读者对 Uniswap v3 机制和投资策略选择有更深入的理解。在阅读本翻译同时，可以随时参考原文以获取更多详细信息。

Uniswap 收益凸性风险的非线性 / Theta-Gamma 波动性。https://www.math3d.org/WvsEXvTWD

简而言之：

展示了对 Uniswap v2 和 v3 的希腊解决方案
在交互式 desmos 文件中提供了使用 Uniswapv3 对亚洲期权、欧式期权和 Bachelier 期权进行对冲的解决方案。
展示了使用 desmos 对 LP 对冲积累策略。
解释了导致 LVR 的历史和替代推导。

希腊参数 - Uniswap v2

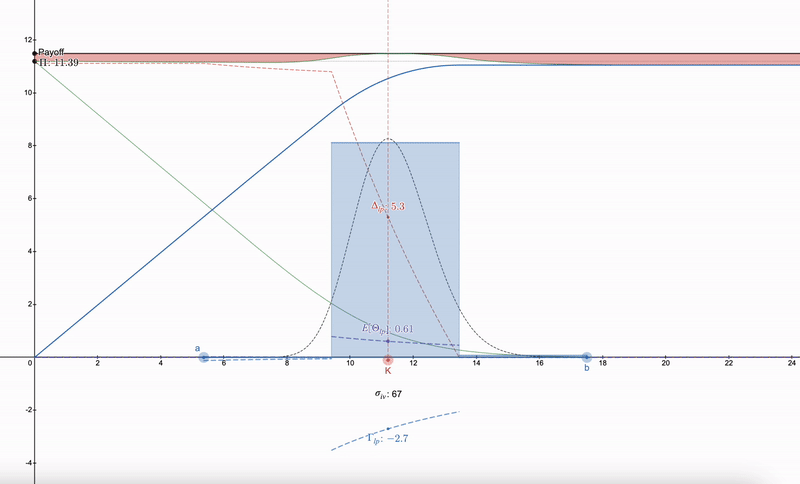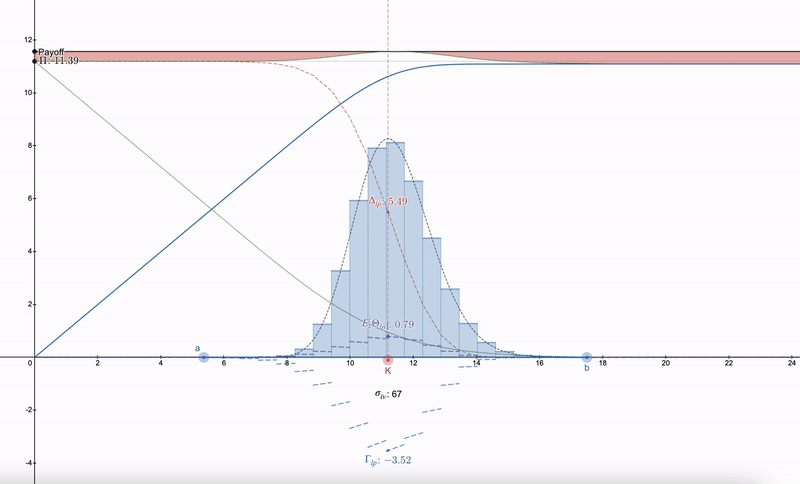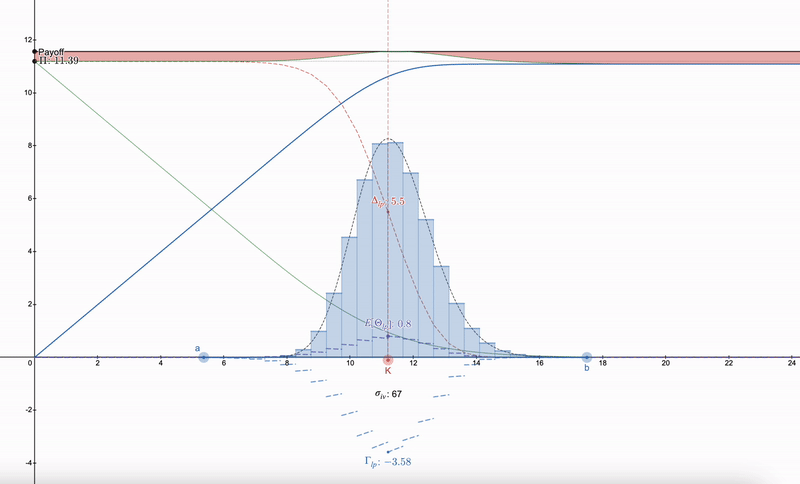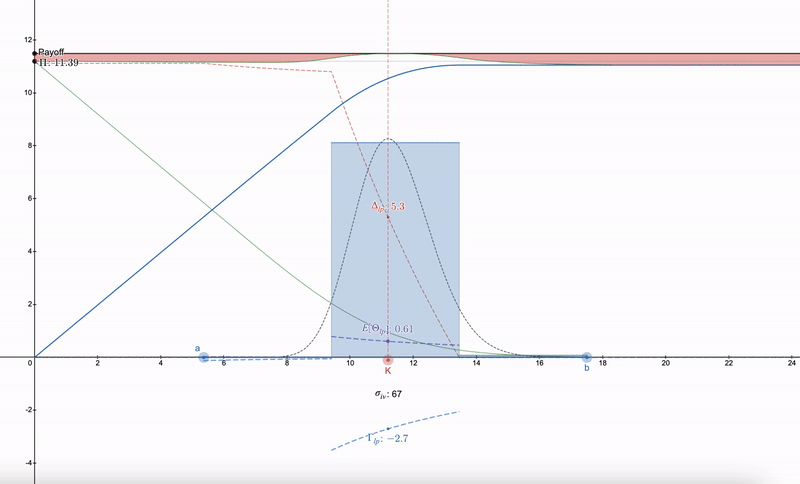
与其将 100% 分配给 LP 头寸，不如将部分分配给 X 资产的做法，其余部分用于做空 X 资产以减少但不消除发散损失。结果是将支付结构从悬崖转换为山丘，如 Guillaume Lambert 所示：希腊参数告诉人们 LP 头寸的价值相对于另一变量（例如，时间，波动率和利率）的敏感性。我们在第 4 部分中介绍了 Delta 和 Gamma。LP 希腊参数很有用，因为你可以将它们与期权的希腊参数匹配，以抵消价格分歧，例如，当价格波动、波动率变化或时间流逝时的效应，即 delta 和 gamma。希腊参数的数值告诉我们各种因素对 LP 头寸价格的影响。

v2 的交互式 desmos 文件：https://www.desmos.com/calculator/inwy6djhhm

需要注意的是，与期权相比，Uniswap 的希腊参数在 LP 头寸价格下跌时会趋向于无穷，如上图中在 x=0 处以虚线表示。为了削减这些尾部风险，我们可以使用 v3 中的集中范围。

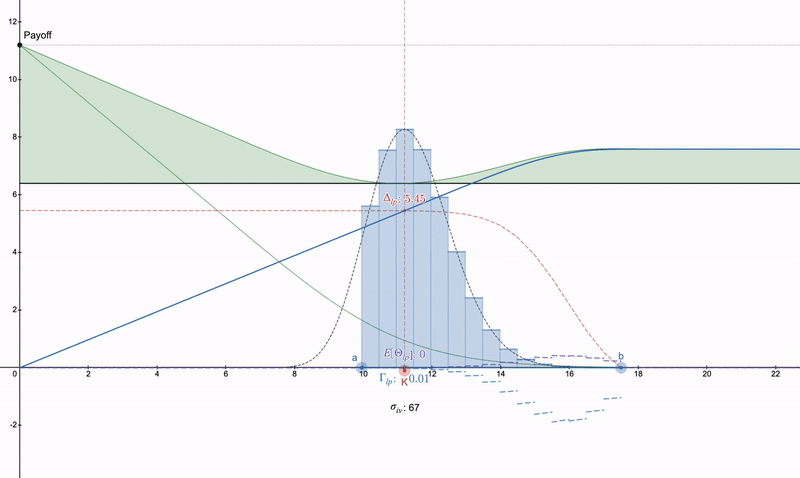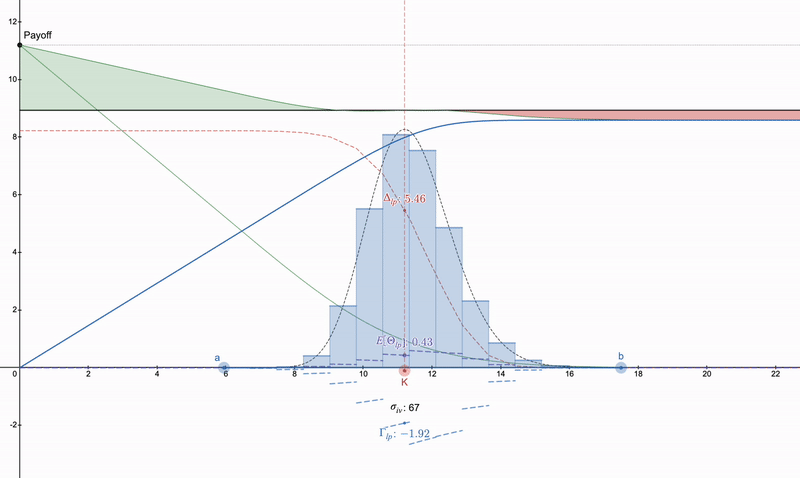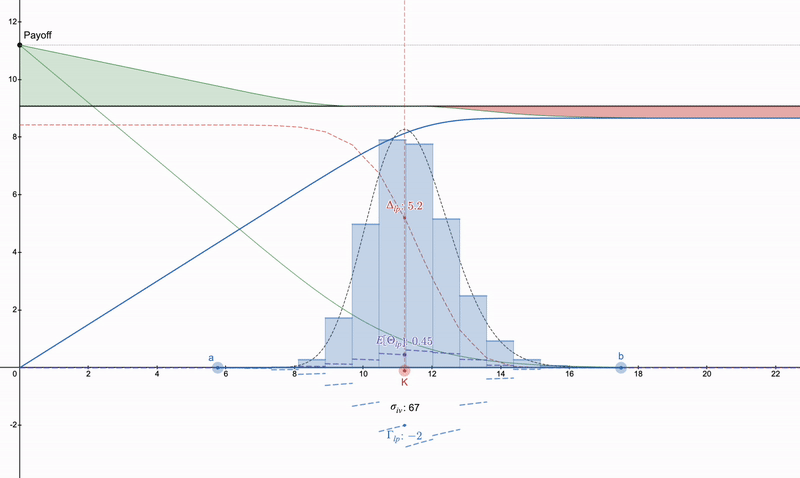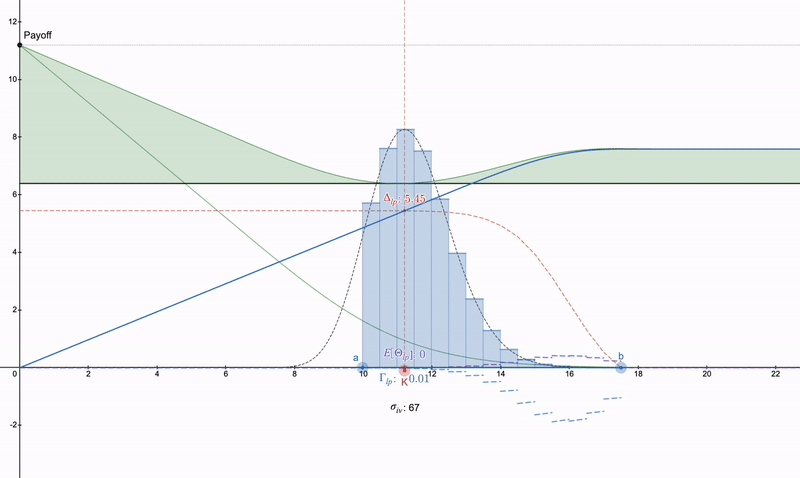
希腊参数 - 集中 LP 范围 v3

univ3 希腊参数的 desmos 文件：https://www.desmos.com/calculator/l8sqzlwkf5

我们将范围 pa （下限）~pb （上限）集中得越小，我们的 Delta Δ 和 Gamma Γ 就越敏感，注意 Gamma 为负，这意味着我们的 LP 支付具有凹形黑色形状。我们的 theta /Θ / 预期费用也会增加，而利率敏感度 ρ 基本上不受影响。

但是，虽然单个 LP 头寸的支付图可能与期权匹配，但其他希腊参数可能不匹配。

LP 希腊参数看起来不像常规期权：https://www.desmos.com/calculator/nyuw7sybin

在这里，我们有一个单个 LP 范围的认购期权，但其他希腊参数并不是固定的。

可以使用的技巧是，与其试图找到对冲 LP 头寸的方法，人们首先需要在市场上找到一个具有执行价格（K）以及隐含波动率（σiv）和到期时间（t）的期权。之后，可以构建一个遵循对数正态分布的一系列 LP 头寸，最初是受丹·罗宾逊（Dan Robinson）对 Uniswap v3 的正态分布流动性指纹启发的^[1]。LP 头寸在价格空间上匹配对数正态分布的粒度化允许对希腊参数进行平滑处理：

请注意，LP 希腊语开始类似于期权。随着价格的下降，LP 头寸的多样性使人们可以切换到下一个范围。超过 7 个 LP 头寸会带来收益的递减。

奇怪的是，使用对数正态分布 100％取消支付似乎非常困难（如果我错了，请纠正我），但是如果对数正态流动性指纹逼近 Dirac Delta 函数，则上述差异（上图中以红色可视化）会消失。例如，亚洲期权恰好也遵循对数正态分布，但令人意外的是，它对价格更敏感，其中 Δ 和 Γ 更加锐利，因为亚洲期权的波动率为常规期权的 1/√3，因此对支付分歧的影响较小：

使用欧式看跌期权对冲 LP 头寸组合以使用其等价的亚洲看跌期权进行对冲。

一个 LP 头寸可以大致匹配欧式期权，但会忽略平滑的希腊参数，而一系列 LP 头寸会平滑希腊字母却会留下一个山丘。这种权衡可能在未来通过潜在的调整 / 偏斜流动性指纹得到改善。

LP 对冲策略

另一方面，如果一个人不感兴趣尝试取消凹形 LP 支付，那么 desmos 文件: https://www.desmos.com/calculator/khvbqzncg9。也可以用于查看各种支付方式的工作原理。下面是可能出现的一系列支付的示例。

垂直看跌价差>>看跌期权>>某种长跨式。请注意，由于 theta 衰减，看跌期权将随着时间的推移而加剧，而 LP 头寸可以由于费用而增长。

我注意到 v3 的一个有趣特性是，如果将 pa 的流动性集中在当前价格的正好 75% 或更低，并将 pb 设为当前价格，那么 X 资产的价值会在 25% 处达到峰值，这对于试图积累资产的人可能具有一定的战略价值。

Dan Robinson 的 v3 工具：https://twitter.com/danrobinson/status/1430678225945042945

可以将这样的单个范围与市场看跌期权结合使用，以获得以下支付：https://www.desmos.com/calculator/a8y3pl3t03：

可以从市场中提取看跌期权参数。随着时间的推移，如果价格不降低足够快，期权的价值将下降。

这样的策略本质上是为了谋求价格下跌以便未来积累资产并赚取费用。需要注意的是，如果没有期权，这将变成一种更具风险的方法，只有在执行者对资产反弹有非常坚定的信念时才有意义。不过，请注意，这并不构成任何财务建议，我只是在做数学运算。

历史深入挖掘导致 LVR：

在第 4 部分中，我指出了 LP 头寸的凹形和收益之间的关系，并希望从历史和 LP 发散损失 / 损失与再平衡（LVR）的角度加以扩展。

Taleb 指出，第一个写下风险和回报的非线性关系的人是 Louis Bachelier ^[2]在 1900 年的 Theory de la Speculation^[3]中归因于它与 Fourier 的热方程的相似之处。巧合的是，Lambert 使用 Feynman-Kac 的方法来解决集中的 LP 头寸的价值^[4]。

「Theory de la Speculation」的第 46 页。一个常数被平方，一个 dt 和一个 dx²！

Bachelier 的方程只是一种略微重新排列的 Black-Scholes-Merton 方程，其中漂移率设置为零^[5]。

资产价格随时间的变化与波动率和曲率有关。

LHS 是 theta-Θ，RHS 是曲率 gamma Γ，由于负号，它恰好是凹形的。然后，零 Angeris，Evans 和 Chitra^[6] 指出，AMM 的 LP 头寸必须具有凹形支付函数。从 Curve 的 CSMM^[7] 到 Forgy＆Lau^[8]的整个对称流动性曲线空间，所有 LP 都应该是凹形的。

根据我们右侧方程中的凹平等性，这意味着做市商（LP）头寸本身必须有溢价。如果没有溢价，下面的平等就会被违反，并且可以通过简单地借用这样一个 LP 头寸并且买入部分标的资产来构建永续多头跨式交易，并等待波动率的增加来加以利用。

Bachelier 等价 / BSM 动态对冲 - 称为凹形命令收益，而凸性命令成本。数学表示：

收益 ∝ 风险乘以凹性（负凸性）。附录中的 BK 推导。

在求解 Uniswap 的 Theta 希腊值^[9]，我注意到通过将 LP 仓位的二阶导数代入上述公式，可以得到与 LVR 相同的方程^[10]。

公式 16。如果 Bachelier 等价中的 Gamma 为 -L/2sqrt(x)³，就会得到相同的结果。

LVR 论文图 2 从上述不变的 xy=k 图中推导出了 vol²/8 LVR 关系，该图导致了凹形 LP 收益。

这并非巧合，来自不同角度的人都得出了相同的结论。Lambert 实际上包含了漂移率^[11]，而其他人则将其排除在外^[12]。

请注意，所有这些模型都假设高斯分布，最初源自伊藤引理中的布朗运动（BM）^[13]，这使我们得到了内部的 -σ²/2 项，该项也出现在 Angeris、Evans 和 Chitra 的最终方程中^[6]，但我们知道，数字资产，包括稳定币，表现出 Hurst 指数>0.5，暗示分形 BM 行为^[14]，Sepp 和 Rakhmonov 也指出，随机波动率方法适用于数字资产的偏斜隐含波动率结构^[15]。

通过审查最持久数字资产的对数 - 对数直方图的尾端收益，我们还看到了非高斯尾部。