零知识证明的力量:深入理解 zk-SNARK
编译:DODO Research
作者:0xAlpha Co-founder @DeriProtocol
介绍
zk-SNARK,即“零知识简洁非交互式知识论证”,使得一名验证者 能够确认一名证明者 拥有某些特定知识,这些知识被称为 witness,满足特定的关系,而无需透露关于见证本身的任何信息。
- 为特定问题生成 zk-SNARK 包括以下四个阶段:
- 将问题(或函数)转换成算术门电路。
- 然后将这个电路翻译成矩阵公式。
- 这个矩阵公式进一步转换成一个多项式,这个多项式应该能被一个特定的最小多项式整除。
最后,这种可整除性在有限域的椭圆曲线点中表示出来,证明就在这里进行。
前三个步骤仅仅是转换了原始陈述的表示方式。最后一个步骤使用同态加密将第三步的陈述投影到加密空间中,使得证明者能够证实其中的镜像陈述。鉴于这种投影利用了非对称加密,从第三步的陈述回溯到原始陈述是不可行的,确保了零知识的暴露。
阅读本文所需的数学背景相当于 STEM 专业学生的大一级代数水平。唯一可能具有挑战性的概念可能是椭圆曲线加密。对于不熟悉这一点的人来说,可以将其视为具有特殊基数的指数函数,同时要记住其逆函数仍然未解。
本文将遵循以下符号规则:
矩阵:粗体大写字母,例如A;显式形式写作
向量:带箭头的小写字母,显式形式写作[ ] ;默认情况下所有向量均为列向量
标量:常规字母表示
让我们用这个问题作为例子:
f(x)=x^3+x^2+5 (1)
假设爱丽丝想要证明她知道一个 。我们将逐步介绍爱丽丝为她的证明生成 zk-SNARK 所需采取的整个程序。
这个问题可能看起来太简单,因为它不涉及控制流(例如,if-then-else)。然而,将带有控制流的函数转换为算术表达式并不困难。例如,让我们考虑以下问题(或在编程语言中的“函数”):
f(x, z):
if(z==1):
return xxx+xx+5
else:
return xx+5
将这个问题重写为以下算术表达式很容易(假设z属于(0,1) ),这并不比方程式 (1) 复杂多少。
f(x,z)=(z-1)(x^2+5)+z(x^3+x^2+5)
在本文中,我们将继续使用方程式 (1) 作为讨论的基础。
第1步:算术门电路
方程式 (1) 可以分解为以下基本算术运算:

这对应于以下算术门电路:

我们还将方程式 (2) 称为一组4个“一级约束”,每个约束描述了电路中一个算术门的关系。通常,一组 n 个一级约束可以概括为一个二次算术程序(QAP),接下来将进行解释。
第2步:矩阵
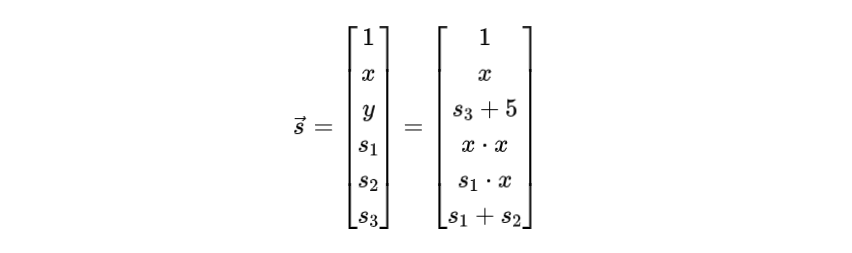
其中y, s1,s2,s3 与方程式 (2) 中定义的相同。
通常,对于一个有m个输入和n个算术门的问题(即 n-1 个中间步骤和最终输出),这个见证向量将是(m+n+1)维的。在实际问题中,数字n可能非常大。例如,对于哈希函数,n通常是几千。
接下来,让我们构造三个 n(m+n+1) 矩阵A,B,C,以便我们可以将方程式 (2) 重写如下:

方程式 (3) 只是方程式 (2) 的另一种表示形式:每组(ai,bi,ci)对应于电路中的一个门。我们只需要明确地展开矩阵公式就可以看到这一点:

我们跳过了构建(A,B,C)的步骤,其实这些步骤相对简单直接。我们只需要根据相应的一级约束,把它们转换成矩阵形式,从而确定(A,B,C)每一行的内容,即(ai,bi,ci)。以第一行为例:可以很容易地看出,要使第一个一级约束 x与x 相乘等于 s1 成立,我们需要的是将[0,1,0,0,0]、[0,1,0,0,0] 和[0,0,0,1,0,0]与向量s相乘。
因此,我们已经成功地把算术门电路转换成了矩阵公式,即方程式 (3)。同时,我们也把需要证明掌握的对象,从 转变为了见证向量s。
第3步:多项式
现在,让我们构造一个 n(n+m+*1) 矩阵PA,它定义了一组关于z的多项式:


这些是六个变量的四组线性方程,可以用传统方法求解。然而,在这种情况下解决 PA 的更有效方法是拉格朗日插值,它利用了问题的特殊性。这里我们跳过求解 PA 的过程,虽然有点繁琐但很直接。

其中:

\begin{bmatrix} \begin{bmatrix} 1,z,z^2,z^3\end{bmatrix}\boldsymbol PA|{z=1}\ \begin{bmatrix} 1,z,z^2,z^3\end{bmatrix}\boldsymbol PA|{z=2}\ \begin{bmatrix} 1,z,z^2,z^3\end{bmatrix}\boldsymbol PA|{z=3}\ \begin{bmatrix} 1,z,z^2,z^3\end{bmatrix}\boldsymbol PA|{z=4}\ \end{bmatrix} " data-formula-type="block-equation" data-mce-style="margin: 0px; padding: 0px; outline: 0px; max-width: 100%; color: #000000; font-family: 'PingFang SC', 'Helvetica Neue', Helvetica, Arial, 'Hiragino Sans GB', 'Heiti SC', 'Microsoft YaHei', 'WenQuanYi Micro Hei', sans-serif; font-style: normal; font-variant-ligatures: normal; font-variant-caps: normal; font-weight: 400; letter-spacing: normal; orphans: 2; text-align: left; text-indent: 0px; text-transform: none; widows: 2; word-spacing: 0px; -webkit-text-stroke-width: 0px; white-space: normal; background-color: #ffffff; text-decoration-thickness: initial; text-decoration-style: initial; text-decoration-color: initial; font-size: 22px; overflow: auto; line-height: 2;">第4步:椭圆曲线点
将方程式 (4) 重写为:

其中i(z)=1只是z的一个平凡的零次多项式,用来使方程统一——所有项都是二次的。这样做的必要性很快就会变得清晰。注意这个方程只包含z的多项式的加法和乘法。

接下来,我们将更详细地阐述实际的操作步骤。
椭圆曲线加密
椭圆曲线的一般理论远远超出了本文的范围。就本文的目的而言,椭圆曲线被定义为从素域Fp映射到E函数,其中E包括满足y^2=x^3+ax+b的点(称为椭圆曲线点,简称 ECPs)。
请注意,虽然到目前为止我们一直在讨论常规算术,但现在当我们转换到素域时,数字的算术运算是以模运算的方式进行的。例如a+b=a+b(mod p),其中p是Fp的阶。
另一方面,两个椭圆曲线点的加法定义如下图所示:

具体来说,两个 ECPs P和Q的加法:
找到直线PQ和曲线R的交点 ,定义为-(P+Q)
翻转到曲线上R的“镜像”点R'。
因此我们定义椭圆曲线点的加法P+Q=R':
请注意,这个规则也适用于特殊情况,即一个 ECP 自加的情况,此时将使用该点的切线。
现在假设我们随机选择一个点G,并将数字1映射到它上面。(这种“初始映射”听起来有点任意。稍后将进行讨论)。然后对于任n 属于Fp,我们定义:
E(N)=G+G+G+…..+G=G点乘n
这有一个操作表达式。定义+G的操作为“生成器”,记为g。那么上述定义等同于:

对于不熟悉椭圆曲线的人来说,你可以将这种映射类比为一个常规的指数函数,其中基数g代替了实数。算术运算的行为类似。然而,一个关键的区别是g^n的逆函数在计算上是不可行的。也就是说,没有办法计算椭圆曲线版本的 。这当然是椭圆曲线加密的基础。这样的映射被称为单向加密。
。这当然是椭圆曲线加密的基础。这样的映射被称为单向加密。
请注意,给定一个椭圆曲线,由于选择G(因此选择“生成器” g)是任意的(除了 x 轴上的点),有无限种映射方式。选择(G或 g)可以类比为选择指数函数的基数(2^x,10^x,e^x等),这是常识的一部分。

然而,Alice 想要证明的方程式 (5) 是二次形式的,所以线性不够。为了处理二次项,我们需要在加密空间中定义乘法。这被称为配对函数,或双线性映射,接下来将进行解释。
双线性映射

公共参考字符串

整个过程被称作“验证钥”,简称VK。这里只涉及7个椭圆曲线点(ECPs),需要提供给验证方。要注意的是,不管问题里面涉及多少输入和一级约束,VK始终是由7个ECPs构成的。
另外,值得一提的是,“可信设置”以及生成PK和VK的过程,对于一个特定的问题来说,只需操作一次即可。
证明与验证
现在拥有公钥(PK),爱丽丝将计算以下椭圆曲线点(ECPs):
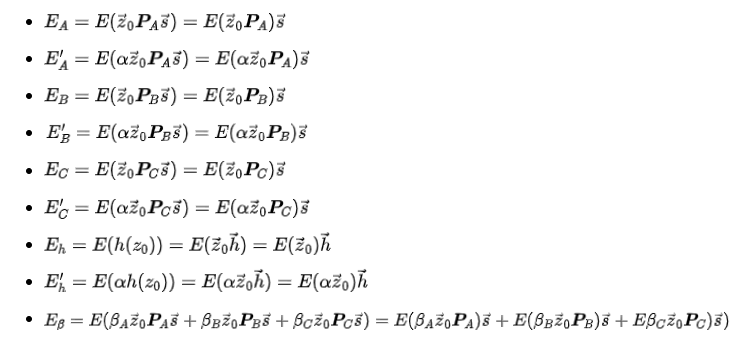
这9个椭圆曲线点就是零知识简洁非交互式证明(zk-SNARK)的关键!
注意,爱丽丝其实只是对公钥里的椭圆曲线点做了些线性组合运算。这点特别关键,验证时会重点检查。
现在,爱丽丝交出了zk-SNARK证明,咱们终于进入验证环节,分三步走。
首先得确认,前8个椭圆曲线点真的是通用参考串里那些点的线性组合。

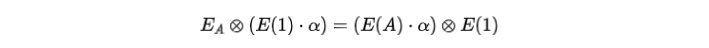
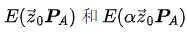 的两个组合。
的两个组合。参考文献
“Zk-SNARKs: Under the Hood” (Vitalik Buterin)
“A Review of Zero Knowledge Proofs” (Thomas Chen, Abby Lu, Jern Kunpittaya, and Alan Luo)
“Why and How zk-SNARK Works: Definitive Explanation” (Maksym Petkus)
Website: Zero-Knowledge Proofs
Wikipedia: Elliptic curve
Wikipedia: Finite field
Wikipedia: Pairing-based cryptography









